Для выбранной модели проверим предпосылку МНК о гомоскедастичности остатков, т. е. о том, что остатки регрессии имеют постоянную дисперсию.

Используем метод Гольдфельдта-Квандта.

1. Упорядочим наблюдения по мере возрастания переменной х.

2. Исключим из рассмотрения 3 центральных наблюдения.

3. Рассмотрим первую группу наблюдений (малые значения фактора х) и

определим 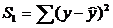этой группы.

4. Рассмотрим вторую группу наблюдений (большие значения фактора х) и определим 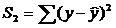этой группы.

5. Проверим, значимо или незначимо отличаются дисперсии остатков этих групп.

Таблица 5

№	x	y	yx	x2	y2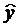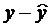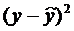
	4,1	14,2	58,22	16,81	201,64	15,47	-1,27	1,60
	5,3	18,4	97,52	28,09	338,56	16,50	1,90	3,61
	7,1	16,4	116,44	50,41	268,96	18,05	-1,65	2,72
	8,5	21,7	184,45	72,25	470,89	19,26	2,44	5,97
	10,2	18,5	188,70	104,04	342,25	20,72	-2,22	4,93
	11,0	22,2	244,20	121,00	492,84	21,41	0,79	0,63
сумма	46,2	111,4	889,53	392,60	2115,14	111,40	0,00	19,46
среднее	7,70	18,57	148,26	65,43	352,52	18,57	0,00	3,89

Определим параметры уравнения регрессии 1 группы:

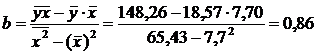
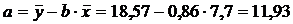
Уравнение регрессии 1 группы:

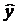=11,93+0,86x

Таблица 6

№	x	y	yx	x2	y2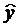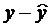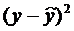
	18,3	28,2	516,06	334,89	795,24	27,56	0,64	0,41
	18,6	26,1	485,46	345,96	681,21	27,85	-1,75	3,06
	19,7	30,2	594,94	388,09	912,04	28,92	1,28	1,63
	21,3	28,6	609,18	453,69	817,96	30,49	-1,89	3,56
	22,1	34,0	751,40	488,41	1156,00	31,27	2,73	7,47
	24,2	32,3	781,66	585,64	1043,29	33,32	-1,02	1,03
сумма	124,2	179,4	3738,70	2596,68	5405,74	179,40	0,00	17,17
среднее	20,70	29,90	623,12	432,78	900,96	29,90	0,00	3,43

Параметры уравнения регрессии 2 группы:

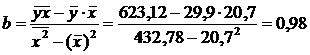
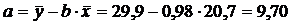
Уравнение регрессии 2 группы:

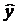=9,7+0,98x

S₁=19.46>S₂=17.17

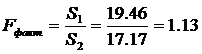
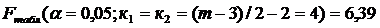
F_факт.< F_табл.

следовательно, остатки гомоскедастичны, предпосылки МНК не нарушены.

5. Рассчитаем прогнозное значение результата у, если прогнозное значение фактора х увеличивается на 5% от его среднего уровня.

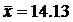
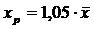
Точечный прогноз:

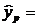11,59+0,87–1,05–14,13=24,515 млн. руб.

Для данной величины выпуска продукции прогнозное значение затрат на производство составляет 24,515 млн. руб.

Для уровня значимости α= 0,05 определим доверительный интервал прогноза.

Предварительно определим стандартные ошибки коэффициента корреляции и параметра b.

Стандартная ошибка коэффициента корреляции:

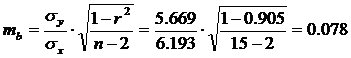
Ошибка прогноза:

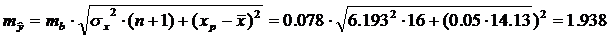
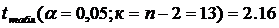
Доверительный интервал прогноза значений y при 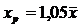с вероятностью 0,95 составит:

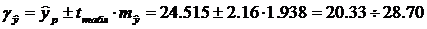
Прогноз надежный, но не очень точный, т. к. .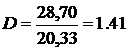

Варианты заданий.

Вариант № 1

Вариант № 2

Вариант № 3

Вариант № 4

Вариант № 5

Вариант № 6

Вариант № 7

Вариант № 8

Вариант № 9

Вариант № 10

Вариант № 11

Вариант № 12

Вариант № 13

Вариант № 14

Вариант № 15

Вариант № 16

Вариант № 17

Вариант № 18

Вариант № 19

Вариант № 20

Вариант № 21

Вариант № 22

Вариант № 23

Вариант № 24

Вариант № 25

Вариант № 26

Вариант № 27

Вариант № 28

Вариант № 29

Вариант № 30

Лабораторная работа № 2.