Нормированный коэффициент корреляции Браве-Пирсона
В качестве оценки генерального коэффициента корреляции р используется коэффициент корреляции r Браве-Пирсона. Для его определения принимается предположение о двумерном нормальном распределении генеральной совокупности, из которой получены экспериментальные данные. Это предположение может быть проверено с помощью соответствующих критериев значимости. Следует отметить, что если по отдельности одномерные эмпирические распределения значений xi и yi согласуются с нормальным распределением, то из этого еще не следует, что двумерное распределение будет нормальным. Для такого заключения необходимо еще проверить предположение о линейности связи между случайными величинами Х и Y. Строго говоря, для вычисления коэффициента корреляции достаточно только принять предположение о линейности связи между случайными величинами, и вычисленный коэффициент корреляции будет мерой этой линейной связи.
Коэффициент корреляции Браве–Пирсона ( 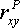 ) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле:
) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле:
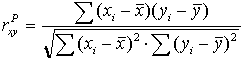
Из формулы видно, что для вычисления 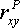 необходимо найти средние значения признаков Х и Y, а также отклонения каждого статистического данного от его среднего
необходимо найти средние значения признаков Х и Y, а также отклонения каждого статистического данного от его среднего 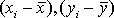 . Зная эти значения, находятся суммы
. Зная эти значения, находятся суммы 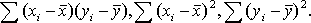 . Затем, вычислив значение
. Затем, вычислив значение 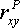 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для f = n –2. Если
, необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для f = n –2. Если 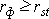 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если
, то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 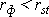 , то между признаками наблюдается недостоверная корреляционная взаимосвязь[2].
, то между признаками наблюдается недостоверная корреляционная взаимосвязь[2].
Пример 1.10 студентам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов.
Решение. Представим исходные данные в виде таблицы 4, в которой введены дополнительные столбцы, необходимые для расчета по формуле.
Таблица 1 – Условия задачи
| № испытуемых | x | y | хi- 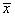 | (хi- 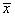 )2 )2 | yi- 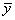 | (yi- 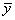 )2 )2 | 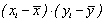 |
| -16,7 | 278,89 | -7,2 | 51,84 | 120,24 | |||
| -3,7 | 13,69 | -17,2 | 295,84 | 63,64 | |||
| -2,7 | 7,29 | -7,2 | 51,84 | 19,44 | |||
| 8,3 | 68,89 | 3,8 | 14,44 | 31,54 | |||
| -7,7 | 59,29 | 2,8 | 7,84 | -21,56 | |||
| -0,7 | 0,49 | 6,8 | 46,24 | -4,76 | |||
| 3,3 | 10,89 | -4,2 | 17,64 | -13,86 | |||
| 3,3 | 10,89 | -7,2 | 51,84 | -23,76 | |||
| 8,3 | 68,89 | 10,8 | 116,64 | 89,64 | |||
| 8,3 | 68,89 | 18,8 | 353,44 | 156,04 | |||
| Сумма | 588,1 | 1007,6 | 416,6 | ||||
| Среднее | 35,7 | 24,2 |
Рассчитываем эмпирическую величину коэффициента корреляции по формуле расчета коэффициента корреляции Браве–Пирсона:
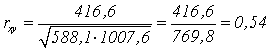
Определяем критические значения для полученного коэффициента корреляции по таблице. При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона число степеней свободы рассчитывается как f = n – 2 = 8. rкрит=0,72 > 0,54 , следовательно, гипотеза Н1 отвергается и принимается гипотеза H0, иными словами, связь между временем решения наглядно-образных и вербальных заданий теста не доказана[1].
