Задача линейного программирования о смесях

Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем – не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в таблице 12.

Таблица 12

Характеристика	Компонент автомобильного бензина
№ 1	№2	№ 3	№4
Октановое число
Содержание серы, %	0,35	0,35	0,3	0,2
Ресурсы, т
Себестоимость, у.е./т

Приказом директора завода-изготовителя установлен следующий расход каждого компонента: 1 – 550 т, 2 – 10 т, 3 – 150 т, 4 – 290 т. Требуется определить, сколько на самом деле тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной. Какова упущенная выгода предприятия при производстве каждых 1000 т бензина при таком решении дирекции?

Ход работы

Пусть 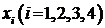– количество в смеси компонента с номером i. С учетом этих обозначений задача минимума себестоимости принимает вид:

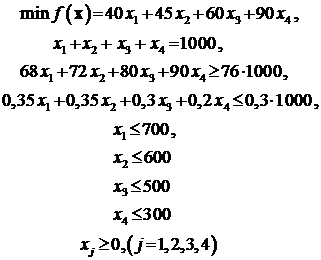
Первое функциональное ограничение отражает необходимость получения заданного количества смеси (1000 т), второе и третье – ограничения по октановому числу и содержанию серы в смеси, остальные – ограничения на имеющиеся объемы соответствующих ресурсов (компонентов). Прямые ограничения очевидны, но принципиально важны для выбора метода решения. Для решения задачи средствами Excel необходимо составить таблицу 13.

Решение задачи о смесях средствами Excel Таблица 13
Переменные	Значения	Критерий и ограничения	Результаты расчетов	Знак отношения	Ресурс
X1		Целевая функция	=40*B3+45*B4+60*B5+90*B6
X2		Ограничение 1	=СУММ(B3:B6)	=
X3		Ограничение 2	=68*B3+72*B4+80*B5+90*B6	=>
X4		Ограничение 3	=0,35*B3+0,35*B4+0,3*B5+0,2*B6	<=
		Ограничение 4	=B3	<=
		Ограничение 5	=B4	<=
		Ограничение 6	=B5	<=
		Ограничение 7	=B6	<=

Для решения задачи средствами Excel нужно воспользоваться программой-надстройкой Поиск решения, расположенной в пункте меню Сервис.

В открывшемся диалоговом окне следует установить:

- адрес целевой ячейки;

- диапазон адресов изменяемых ячеек;

- систему ограничений.

Добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить,Изменить,Удалить. Кнопка Параметры открывает окно, в котором следует установить флажок Неотрицательные решения. Для нахождения оптимального решения следует нажать кнопку Выполнить.

Диалоговое окно Результаты поиска решенияпозволяет:

- сохранить на текущем рабочем листе найденное оптимальное решение;

- восстановить первоначальные значения;

- сохранить сценарий;

- выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения.

Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями.

Оптимальное решение задачи имеет вид:

.

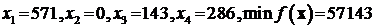Решение дирекции:

.

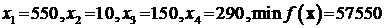Таким образом, упущенная выгода предприятия при производстве каждых 1000 т бензина при таком решении дирекции составляет 407 у.е.

Лабораторная работа №7

Модель Леонтьева

Имеется n отраслей. Рассматривается процесс производства за один год. Обозначим через х_i общий (валовой) объём продукции i-той отрасли, х_ij - объём продукции i-той отрасли, потребляемый j-той отраслью в процессе производства, у_i - объём конечного продукта i-той отрасли для непроизводственного потребления. Выполняются соотношения баланса:

х_i = Σ х_ij + у_i , i = 1,…,n, j = 1,…,n.

Коэффициенты прямых затрат

а_ij = х_ij / х_j

показывают затраты продукции i-той отрасли на производство единицы продукции j-той отрасли. Считаем, что а_ij = const. Тогда х_ij = а_ij · х_j , то есть

х_i = Σ а_ij · х_j + у_i .

Если обозначить вектор валового выпуска через

X= ,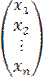

матрицу прямых затрат через

А = ,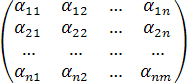

а вектор конечного продукта через

У= ,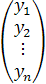

то получаем матричное уравнение: Х = АХ + У.

Матрица А ≥ 0 (все элементы неотрицательны) называется продуктивной, если для любого вектора У ≥ 0 существует решение Х ≥ 0 этого уравнения. Модель Леонтьева в этом случае также называется продуктивной.

Условие продуктивности матрицы А: наибольшая из сумм элементов в столбцах матрицы А не превосходит 1, причем в А есть хотя бы один столбец, сумма элементов которого меньше 1.

Задание

Выяснить продуктивность модели Леонтьева, учитывая схему:

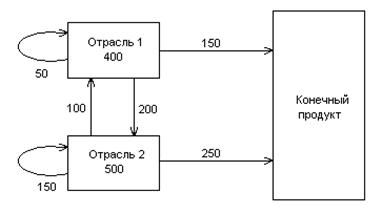
Ход работы

По условию х₁ = 400, х₂ = 500, у₁ =150, у₂ = 250, х₁₁ = 50, х₁₂ = 200,
х₂₁ = 100, х₂₂ = 150.

1. Находим элементы а_ij = х_ij / х_j матрицы А средствами Excel:

А = =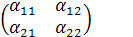

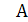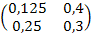
2. Вычисляем максимум сумм элементов в столбцах матрицы А:

max (0,125 + 0,25; 0,4 + 0,3) = 0,7 < 1 А - продуктивная матрица.

3. Пусть новый вектор валового выпуска

Х = ,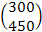

тогда из равенства Х=АХ+У получаем формулу для определения соответст­вующего вектора конечного продукта:

У = Х – АХ = (Е – А)Х =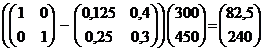

Замечание: действия с матрицами выполняем средствами Excel. Для выполнения вычитания матриц, стоящих в скобках, необходимо разместить обе матрицы в некоторых диапазонах и определить диапазон для размещения результата вычислений. Затем в левую верхнюю ячейку новой матрицы ввести формулу для вычисления (например, для вычитания матриц) «=A1- A5» и скопировать ее методом протягивания в остальные ячейки диапазона, отведенного под результат. Для выполнения умножения матриц нужно выделить на рабочем листе блок ячеек под матрицу – произведение 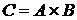. Размер этой матрицы в данном случае будет 2×1. Затем следует воспользоваться функцией МУМНОЖ из категории Математические. В качестве аргументов этой функции указать диапазоны перемножаемых матриц и нажать сочетание клавиш CTRL+SHIFT+ENTER.

4. Зададим новый вектор конечного продукта

У =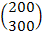

и найдем соответствующий вектор валового выпуска

Х = (Е – А)^-1 У = .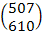

Матрица (Е – А)^-1 называется матрицей полных затрат и определяется так: на рабочем листе нужно выделить блок ячеек под обратную матрицу 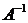и воспользоваться встроенной функцией МОБРиз категории Математические. В качестве аргумента этой функции указать диапазон исходной матрицы 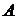и нажать сочетание клавиш CTRL+SHIFT+ENTER.

Варианты на решение задачи о продуктивности модели Леонтьева

х1
х2
х11
х12
х21
х22

Лабораторная работа №8

Фильтрация списков

Задание. При работе с базами данных важно иметь возможность быстро находить нужную информацию. Допустим, у вас имеется список телефонных номеров или таблица ассортимента товаров, и вам требуется, например, выбрать номера одной АТС или все коды моделей факсов. Конечно же, вам не захочется просматривать весь список и выписывать необходимую информацию. С помощью имён в полях вашего списка вы можете автоматически отфильтровать и вывести на экран только нужные вам данные.

Ход работы

1. Подготовьте данные к фильтрации. Создайте таблицу Ассортимент. Для этого вам необходимо создать лист Microsoft Excel и заполнить поля в соответствии с таблицей 14:

Таблица 14

А	B	C	D	E	F	G
1	Товар	Модель	Название	Цена (тыс.руб)	Кол-во	Сумма
	Ксерокс	C100 GLS	Персональный	827.00	564.00	466 428.00
	Ксерокс	C110 GLS	Персональный	993.00	623.00	618 639.00
	Ксерокс	C200 GLS	Персональный Плюс	1 430.00	568.00	812 240.00
	Ксерокс	C210 GLS	Персональный Плюс	1 716.00	269.00	461 604.00
	Ксерокс	C300 GLS	Деловой	2 470.00	412.00	1017 640.00
	Ксерокс	C310 GLS	Деловой	2 698.00	574.00	1 548 52.00
	Ксерокс	C400 GLS	Профессиональный	4 270.00	223.00	952 210.00
	Ксерокс	C410 GLS	Профессиональный	5 124.00	652.00	3 340 48.00
	Ксерокс	C420 GLS	Профессиональный	6 415.00	895.00	5 741 25.00
	Факс	F100 G	Персональный	7 378.00	154.00	1 136 12.00
	Факс	F150 G	Персональный	1 608.00	214.00	344 112.00
	Факс	F200 G	Персональный Плюс	1 840.00	235.00	432 400.00
	Факс	F250 G	Персональный Плюс	1 730.00	221.00	382 330.00
	Факс	F300 G	Деловой	2 076.00	541.00	1 123 16.00
	Факс	F350 G	Деловой	2 551.00	544.00	1 387 44.00
	Факс	F400 G	Профессиональный	2 761.00	53.00	146 333.00
	Факс	F450 G	Профессиональный	3 513.00	542.00	1 904 46.00
	Факс	F500 G	Профессиональный	4 878.00	325.00	1 585 50.00

Значения колонки Сумма получаютпутём умножения значений столбца Цена на значения столбца Количество: в ячейке G2 поставьте знак «=», затем выделите значение ячейки F2, поставьте знак умножения и далее значение ячейки Е2, нажмите Enter. Получив число, протяните мышкой до конечной ячейки столбца G.

Вы получили полную таблицу данных, в которой вы будете проводить фильтрацию.

2. Выделите ячейку В1. В меню Данные (Data)выберите команду Фильтр-Автофильтр (Filter-AutoFilter).В заголовках каждого столбца появятся кнопки фильтра со стрелочками вниз.

Примечание.В некоторых базах данных при этом появляется диалоговое окно, спрашивающее, хотите ли вы использовать верхнюю строку в качестве заголовка. В диалоговом окне щёлкните на кнопке ОК.

3. Щёлкните на стрелке фильтра в ячейке D1. Это заголовок Название. В появившемся окне списка критериев необходимо выбрать нужный критерий (ключ) фильтрации.

Название

(Все)

(Первые 10…)

Деловой

Персональный

Критерии фильтрации находятся в списке в алфавитном порядке.

4. В качестве ключа фильтрации в ячейке D1 выделите слово Персональный.

В списке останутся только названия факсов и ксероксов, включающие слово «Персональный». Все остальные записи таблицы не удалены, а лишь временно скрыты. Порядковые номера строк в списке теперь не являются последовательными:

Таблица 15

Товар	Модель	Название	Цена (тыс.руб)	Кол-во	Сумма
Ксерокс	C100 GLS	Персональный
Ксерокс	C110 GLS	Персональный
Факс	F100 G	Персональный
Факс	F150 G	Персональный

5. Щёлкните на кнопке со стрелкой в ячейке В21 (табл. 15). Выделите в списке ключ Ксерокс. Список персональных ксероксов станет видимым на вашем рабочем листе. Чтобы снова вывести на экран полный список, нужно щёлкнуть на любой кнопке со стрелкой фильтра, и в списке критериев фильтрации выделить строку Все (All). Или в меню Данные (Data)выбрать команду Фильтр – Показать все (Filter – Show All).

6. Восстановите список. В меню Данныевыберите команду Фильтр - Отобразить всё. Теперь на рабочем листе снова находится полный список товаров.

7. Составьте список десяти наиболее доходных видов товаров.

В поле Суммаустановите критерий фильтрации Первые 10 (Тор 10). Появится диалоговое окно Наложение условия по списку(Тор10 AutoFilter).

Убедитесь, что параметры окна в группе Вывестиустановлены так: «10», «наибольших», «элементов списка», и щёлкните на кнопке ОК.

На рабочем листе останется список товаров, значения в поле Сумма которых составляют десять наибольших в полном списке величин.

Восстановите полный список, выбрав команду Фильтр - Отобразить всё в меню Данные.

8. Задайте свои критерии поиска данных.

В этом упражнении вы составите список ксероксов и факсов с названиями «Персональный» и «Персональный Плюс».

Щёлкните на стрелке фильтра поля Название. В списке ключей выберите Условие. Откроется диалоговое окно Пользовательский автофильтр (Custom AutoFilter). Убедитесь, что в группе Названиев верхнем поле операторов находится слово «равно». Щёлкните на стрелке соседнего поля и выделите строку Профессиональный. Включите опцию ИЛИ (OR). Щёлкните на стрелке нижнего поля операторов и выделите «равно». Щёлкните на стрелке нижнего поля критериев и выделите строку Персональный Плюс. Нажмите ОК.

Библиографический список

1. Демиденко Е.З.Линейная и нелинейная регрессия. – М.: Финансы и статистика, 2001. - 302 с.

2. Приходько А.И. Регрессионный анализ средствами EXCEL: учебное пособие. – Ростов-на-Дону: Издательство «Феникс», 2007. – 250 с.

3. Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М. Экономико-математические методы и прикладные модели: учебное пособие. – Москва: ЮНИТИ, 2002. - 388с.

4. Шалабанов А.К., Роганов Д.А. Эконометрика: учебно-методическое пособие. – Казань: Академия управления «Тисби», 2004. - 133 с.

Приложение

Квантили распределения величины v = 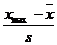или v =

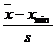
Таблица 1

q 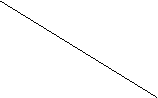n	0.10	0.05	0.025	0.01
	1.406	1.412	1.414	1.414
	1.645	1.689	1.710	1.723
	1.791	1.869	1.917	1.955
	1.894	1.996	2.067	2.130
	1.974	2.093	2.182	2.265
	2.041	2.172	2.273	2.374
	2.097	2.237	2.349	2.464
	2.146	2.294	2.414	2.540
	2.190	2.343	2.470	2.606
	2.229	2.387	2.519	2.663
	2.264	2.426	2.562	2.714
	2.297	2.461	2.602	2.759
	2.326	2.493	2.638	2.800
	2.354	2.523	2.670	2.837
	2.380	2.551	2.701	2.871
	2.404	2.577	2.728	2.903
	2.426	2.600	2.754	2.932
	2.447	2.623	2.778	2.959
	2.467	2.644	2.801	2.984
	2.486	2.664	2.823	3.008
	2.504	2.683	2.843	3.030
	2.520	2.701	2.862	3.051
	2.537	2.717	2.880	3.071

1. Таблица значений функции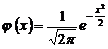

Таблица 2

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9   1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9   2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9   3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9	0,3989   0,2420   0,0540   0,0044

2. Таблица значений функции Лапласа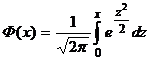

Таблица 3

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0,00	0,0000	0,36	0,1406	0,72	0,2642	1,08	0,3599	1,44	0,4251
0,01	0,0040	0,37	0,1443	0,73	0,2673	1,09	0,3621	1,45	0,4265
0,02	0,0080	0,38	0,1480	0,74	0,2704	1,10	0,3643	1,46	0,4279
0,03	0,0120	0,39	0,1517	0,75	0,2734	1,11	0,3665	1,47	0,4292
0,04	0,0160	0,40	0,1554	0,76	0,2764	1,12	0,3686	1,48	0,4306
0,05	0,0199	0,41	0,1591	0,77	0,2794	1,13	0,3708	1,49	0,4319
0,06	0,0239	0,42	0,1628		0,2823	1,14	0,3729	1,50	0,4332
0,07	0,0279	0,43	0,1664	0,79	0,2852	1,15	0,3749	1,51	0,4345
0,08	0,0319	0,44	0,1700	0,80	0,2881	1,16	0,3770	1,52	0,4358
0,09	0,0359	0,45	0,1736	0,81	0,2910	1,17	0,3790	1,53	0,4370
0,10	0,0398	0,46	0,1772	0,82	0,2939	1,18	0,3810	1,54	0,4382
0,11	0,0438	0,47	0,1808	0,83	0,2967	1,19	0,3830	1,55	0,4394
0,12	0,0478	0,48	0,1844	0,84	0,2995	1,20	0,3849	1,56	0,4406
0,13	0,0517	0,49	0,1879	0,85	0,3023	1,21	0,3869	1,57	0,4418
0,14	0,0557	0,50	0,1915	0,86	0,3051	1,22	0,3888	1,58	0,4429
0,15	0,0596	0,51	0,1950	0,87	0,3079	1,23	0,3907	1,59	0,4441
0,16	0,0636	0,52	0,1985	0,88	0,3106	1,24	0,3925	1,60	0,4452
0,17	0,0675	0,53	0,2019	0,89	0,3133	1,25	0,3944	1,61	0,4463
0,18	0,0714	0,54	0,2	0,90	0,3159	1,26	0,3962	1,62	0,4474
0,19	0,0753	0,55	0,2088	0,91	0,3186	1,27	0,398	1,63	0,4484
0,20	0,0793	0,56	0,2123	0,92	0,3212	1,28	0,3997	1,64	0,4495
0,21	0,0832	0,57	0,2157	0,93	0,3238	1,29	0,4015	1,65	0,4505
0,22	0,0871	0,58	0,2190	0,94	0,3264	1,30	0,4032	1,66	0,4515
0,23	0,0910	0,59	0,2224	0,95	0,3289	1,31	0,4049	1,67	0,4525
0,24	0,0948	0,60	0,2557	0,96	0,3315	1,32	0,4066	1,68	0,4535
0,25	0,0987	0,61	0,2291	0,97	0,3340	1,33	0,4082	1,96	0,4545
0,26	0,1026	0,62	0,2324	0,98	0,3365	1,34	0,4099	1,70	0,4554
0,27	0,1064	0,63	0,2357	0,99	0,3389	1,35	0,4115	1,71	0,4564
0,28	0,1103	0,64	0,2389	1,00	0,3413	1,36	0,4131	1,72	0,4573
0,29	0,1141	0,65	0,2422	1,01	0,3438	1,37	0,4147	1,73	0,4582
0,30	0,1179	0,66	0,2454	1,02	0,3461	1,38	0,4162	1,74	0,4591
0,31	0,1217	0,67	0,2486	1,03	0,3485	1,39	0,4177	1,75	0,4599
0,32	0,1255	0,68	0,2517	1,04	0,3508	1,40	0,4192	1,76	0,4608
0,33	0,1293	0,69	0,2549	1,05	0,3531	1,41	0,4207	1,77	0,4616
0,34	0,1331	0,70	0,2580	1,06	0,3554	1,42	0,4222	1,78	0,4625
0,35	0,1368	0,71	0,2611	1,07	0,3577	1,43	0,4236	1,79	0,4633
1,80	0,4641	1,96	0,475	2,24	0,4875	2,56	0,4948	2,88	0,4980
1,81	0,4649	1,97	0,4756	2,26	0,4881	2,58	0,4951	2,90	0,4981
х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,82	0,4656	1,98	0,4761	2,28	0,4887	2,60	0,4953	2,92	0,4982
1,83	0,4664	1,99	0,4767	2,30		2,62	0,4956	2,94	0,4984
1,84	0,4671	2,00	0,4772	2,32	0,4898	2,64	0,4959	2,96	0,4985
1,85	0,4678	2,02	0,4783	2,34	0,4904	2,66	0,4961	2,98	0,4986
1,86	0,4686	2,04	0,4793	2,36	0,4909	2,68	0,4963	3,00	0,49865
1,87	0,4693	2,06	0,4803	2,38	0,4913	2,70	0,4965	3,20	0,49931
1,88	0,4699	2,08	0,4812	2,40	0,4918	2,72	0,4967	3,40	0,49966
1,89	0,4706	2,10	0,4821	2,42	0,4922	2,74	0,4969	3,60	0,499841
1,90	0,4713	2,12	0,4830	2,44	0,4927	2,76	0,4971	3,80	0,499928
1,91	0,4719	2,14	0,4838	2,46	0,4931	2,78	0,4973	4,00
1,92	0,4726	2,16	0,4846	2,48	0,4934	2,80	0,4974	4,50	0,499997
1,93	0,4732	2,18	0,4854	2,50	0,4938	2,82	0,4976	5,00	0,499997
1,94	0,4738	2,20	0,4861	2,52	0,4941	2,84	0,4977
1,95	0,4744	2,22	0,4868	2,54		2,86	0,4979

3. Критические точки распределения χ²

Таблица 4

Число степеней свободы k	Уровень значимости a
0,01	0,025	0,05	0,95	0,975	0,99
	6,6	5,0	3,8	0,0039	0,00098	0,00016
	9,2	7,4	6,0	0,103	0,051	0,020
	11,3	9,4	7,8	0,352	0,216	0,115
	13,3	11,1	9,5	0,711	0,484	0,297
	15,1	12,8	11,1	1,15	0,831	0,554
	16,8	14,4	12,6	1,64	1,24	0,872
	18,5	16,0	14,1	2,17	1,69	1,24
	20,1	17,5	15,5	2,73	2,18	1,65
	21,7	19,0	16,9	3,33	2,70	2,09
	23,2	20,5	18,3	3,94	3,25	2,56
	24,7	21,9	19,7	4,57	3,82	3,05
	26,2	23,3	21,0	5,23	4,40	3,57
	27,7	24,7	22,4	5,89	5,01	4,11
	29,1	26,1	23,7	6,57	5,63	4,66
	30,6	27,5	25,0	7,26	6,26	5,23
	32,0	28,8	26,3	7,96	6,91	5,81
	33,4	30,2	27,6	8,67	7,56	6,41
	34,8	31,5	28,9	9,39	8,23	7.01
	36,2	32,9	30,1	10,1	8,91	7,63
	37,6	34,2	31,4	10,9	9,59	8,26
	38,9	35,5	32,7	11,6	10,3	8,90
	40,3	36,8	33,9	12,3	11,0	9,54
	41,6	38,1	35,2	13,1	11,7	10,2
	43,0	39,4	36,4	13,8	12,4	10,9
	44,3	40,6	37,7	14,6	13,1	11,5
	45,6	41,9	38,9	15,4	13,8	12,2
	47,0	43,2	40,1	16,2	14,6	12,9
	48,3	44,5	41,3	16,9	15,3	13,6
	49,6	45,7	42,6	17,7	16,0	14,3
	50,9	47,0	43,8	18,5	16,8	15,0

Учебное издание