Пренексная нормальная форма для формул ИП
Формула φсигнатуры Σ называется бескванторной, если она не содержит кванторов. Говорят, что бескванторная формула φнаходится в дизъюнктивной (конъюнктивной) нормальной форме, если она получается из некоторой формулы ψисчисления АВ, находящейся в ДНФ (КНФ) заменой всех пропозициональных переменных x1,…,xnна некоторые атомарные формулы φ1,…,φnсигнатуры Σ соответственно.
Говорят, что формула φсигнатуры Σ находится в пренексной нормальной форме (ПНФ), если она имеет вид Q1x1…Qnxnψ, где Qi,‑кванторы1≤i≤n, а ψ‑бескванторная формула, находящаяся в ДНФ.
Теорема 1. Для любой формулы φсигнатуры Σ существует формула ψсигнатуры Σ, находящаяся в ПНФ и эквивалентная формуле φ.
Пример 1.Формулу χ  =
=  x
x  yφ(x,y)→
yφ(x,y)→  x
x  yψ(x,y)привести к пренексной нормальной форме. считая формулы φи ψатомарными.
yψ(x,y)привести к пренексной нормальной форме. считая формулы φи ψатомарными.
Решение.Избавившись от импликации, получаем χ≡(  x
x  yφ(x,y))∨
yφ(x,y))∨  x
x  yψ(x,y). Используя утверждение 3, пп. а, б утверждения 4 и теорему о замене, получаем χ≡
yψ(x,y). Используя утверждение 3, пп. а, б утверждения 4 и теорему о замене, получаем χ≡  x
x  yφ(x,y)∨
yφ(x,y)∨  x
x  yψ(x,y). Так как в формуле
yψ(x,y). Так как в формуле  x
x  yψ(x,y)переменные х, у являются связанными, то по пп. д, е утверждения 4 имеем χ≡
yψ(x,y)переменные х, у являются связанными, то по пп. д, е утверждения 4 имеем χ≡  x
x  y(φ(x,y)∨
y(φ(x,y)∨  x
x  yψ(x,y)). Пусть u, ∨‑некоторые новые переменные. Тогда по пунктам ж, з утверждения 4 получаем χ≡
yψ(x,y)). Пусть u, ∨‑некоторые новые переменные. Тогда по пунктам ж, з утверждения 4 получаем χ≡  x
x  y(φ(x,y)∨
y(φ(x,y)∨  u
u  vψ(u,v)),откуда по пунктам ж, з утверждения 4 χ≡
vψ(u,v)),откуда по пунктам ж, з утверждения 4 χ≡  x
x  y
y  u
u  v(φ(x,y)∨ψ(u,v)). Формула φ(x,y)∨ψ(u,v)находится в ДНФ, а значит, формула
v(φ(x,y)∨ψ(u,v)). Формула φ(x,y)∨ψ(u,v)находится в ДНФ, а значит, формула  x
x  y
y  u
u  v(φ(x,y)∨ψ(u,v)) находится в ПНФ.
v(φ(x,y)∨ψ(u,v)) находится в ПНФ.
Теорема 2. Все доказуемые в ИПΣ формулы являются тождественно истинными.
Доказательство проводим индукцией по длине вывода формулы. Очевидно, что аксиомы ИПΣ являются тождественно истинными. Проверку того, что правила вывода 1-3 сохраняют тождественную истинность, мы оставляем читателю в качестве упражнения.
Следствие 1. Исчисление ИПΣнепротиворечиво, т.е. не все формулы ИПΣ доказуемы в ИПΣ.
В ИПΣ справедлив аналог теоремы о полноте в исчислении высказываний:
Теорема 3(теорема Геделя о полноте). Формула φисчисления ИПΣ доказуема тогда и только тогда, когда φтождественно истинна.
Таким образом, проверка доказуемости формулы φсводится к проверке ее тождественной истинности. Однако в отличие от ИВ в общем случае не существует алгоритма распознавания доказуемости формул ИПΣ, т. е. ИПΣ неразрешимо. Тем не менее если в формуле φ"записать", что каждая переменная может принимать конечное число значений, то перебором всех возможных систем можно установить, является ли формула тождественно истинной или нет.
Машины Тьюринга
Машина Тьюринга 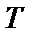 – это система, работающая в дискретные моменты времени
– это система, работающая в дискретные моменты времени 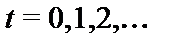 и состоящая из следующих частей:
и состоящая из следующих частей:
конечная лента,разбитая на конечное число ячеек.В каждый момент времени 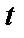 в ячейках записаны буквы из некоторого алфавита
в ячейках записаны буквы из некоторого алфавита 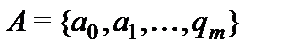 (где
(где 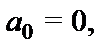
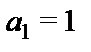 ,
,  ), называемого внешним алфавитом машины.Ячейка, в которой записан символ
), называемого внешним алфавитом машины.Ячейка, в которой записан символ  , называется пустой.Если в какой–то момент времени лента имеет
, называется пустой.Если в какой–то момент времени лента имеет 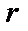 ячеек, то состояние ленты полностью описывается словом
ячеек, то состояние ленты полностью описывается словом  , где
, где  – состояние первой (слева) ячейки,
– состояние первой (слева) ячейки,  – состояние второй ячейки и т.д.
– состояние второй ячейки и т.д.
Управляющая головка, представляющая собой устройство, которое может перемещаться вдоль ленты так, что в каждый рассматриваемый момент времени оно находится напротив определенной ячейки и имеет некоторое состояние 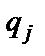 из конечного множества внутренних состояний
из конечного множества внутренних состояний  ,
, 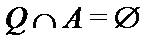 .Состояние
.Состояние  называется заключительными означает завершение работы машины.Состояние
называется заключительными означает завершение работы машины.Состояние 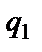 называетсяначальным и означает начало работы машины.
называетсяначальным и означает начало работы машины.
ПрограммаΠ, т.е. совокупность выражений 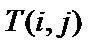 (где
(где 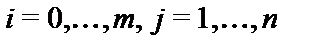 ), называемых командами, каждое из которых имеет один из следующих видов:
), называемых командами, каждое из которых имеет один из следующих видов:

сдвиг головки, находящейся в состоянии 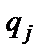 напротив ячейки с буквой
напротив ячейки с буквой  , на одну ячейку влево с заменой состояния
, на одну ячейку влево с заменой состояния 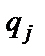 на
на 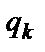 ;
;
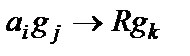
сдвиг головки, находящейся в состоянии 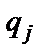 напротив ячейки с буквой
напротив ячейки с буквой  , на одну ячейку вправо с заменой состояния
, на одну ячейку вправо с заменой состояния 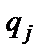 на
на  ;
;
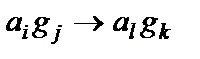
замена буквы  в текущей ячейке на букву
в текущей ячейке на букву  , а также замена состояния
, а также замена состояния  головки на состояние
головки на состояние 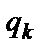
Замечание 1.1) Команды не могут начинаться со слов 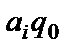 .
.
2) 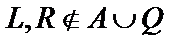 .
.
Таким образом, машина Тьюринга– это пятерка 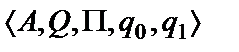 .
.
Машинным словом называется слово 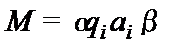 , где
, где  – состояние ленты,
– состояние ленты,  – состояние головки, находящейся напротив ячейки с состоянием
– состояние головки, находящейся напротив ячейки с состоянием 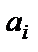 , занимающей то же положение среди других ячеек, что и буква
, занимающей то же положение среди других ячеек, что и буква 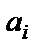 в слове
в слове 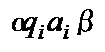 .
.
Пустое слово обозначим через 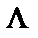 .
. 
Опишем преобразование 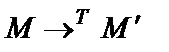 машинного слова
машинного слова  в машинное слово
в машинное слово 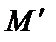 за один шаг работы машины
за один шаг работы машины 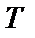 :
:
если 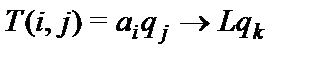 , то
, то 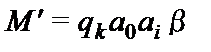 при
при 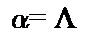 и
и 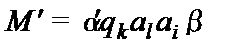 при
при  ;
;
если 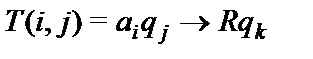 , то
, то  при
при  и
и 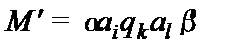 при
при 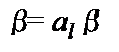 ;
;
если  , то
, то  .
.
Машинное слово 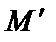 получается из машинного слова
получается из машинного слова  с помощью машины Тьринга
с помощью машины Тьринга 
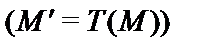 , если существует последовательность преобразований
, если существует последовательность преобразований  ,
, 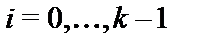 , для которой
, для которой  ,
, 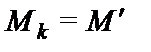 .
.
Пусть 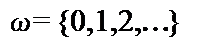 – множество натуральных чисел с нулем,
– множество натуральных чисел с нулем, 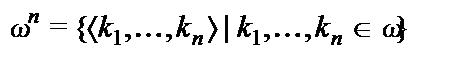 .
.
Частичная функция – это отображение 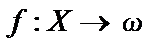 , где
, где 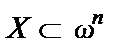 .Если
.Если  , то частичная функция
, то частичная функция 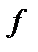 называется всюду определенной. Если
называется всюду определенной. Если 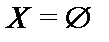 , то частичная функция
, то частичная функция 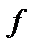 называется нигде ен определенной.
называется нигде ен определенной. 
Для любого числа 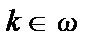 через
через  обозначим слово, состоящее из
обозначим слово, состоящее из 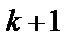 числа единиц:
числа единиц: 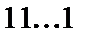 .Для любой
.Для любой 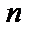 –ки
–ки  слово
слово 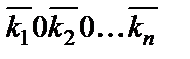 называется записью этой
называется записью этой 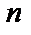 –ки.
–ки.
Частичная функция 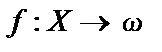 , где
, где 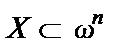 , называется вычислимой по Тьюрингу, если существует машина Тьюринга
, называется вычислимой по Тьюрингу, если существует машина Тьюринга 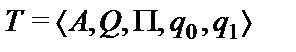 такая, что
такая, что
1) 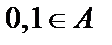 ;
;
2)машина  применима к записи
применима к записи 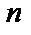 –ки
–ки 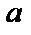
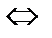
 ;
;
3) 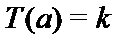 для
для 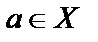 и
и  .
.
Пример 1.Построим машину Тьюринга  , вычисляющую функцию
, вычисляющую функцию  .Пусть
.Пусть  , где
, где  ,
, 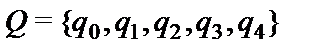 , программа Π состоит из команд:
, программа Π состоит из команд:






