Истинность формулы ЛП в алгебраической системе.
Дадим индуктивное определение истинности формулы φ(x1,…,xn) сигнатуры Σ на элементах a1,…,an 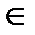 Ав алгебраической системе
Ав алгебраической системе  =
= 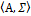 .
.
Запись  ╞φ(a1,…,an)будет означать, что формула φистинна на элементах a1,…,an
╞φ(a1,…,an)будет означать, что формула φистинна на элементах a1,…,an 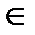 Ав системе
Ав системе  .
.
1)  ╞t1(a1,…,an)=t2(a1,…,an), где t1,t2
╞t1(a1,…,an)=t2(a1,…,an), где t1,t2 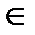 T(Σ),
T(Σ), 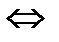 значения термов t1,t2 в системе Ãна элементах a1,…,an
значения термов t1,t2 в системе Ãна элементах a1,…,an 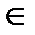 А совпадают;
А совпадают;
2)  ╞P(t1(a1,…,an),….,tk(a1,…,an)),гдеP(k)
╞P(t1(a1,…,an),….,tk(a1,…,an)),гдеP(k) 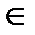 Σ,t1,…,tk
Σ,t1,…,tk 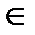 T(Σ),↔(t1(a1,…,an),…, tk(a1,…,an))
T(Σ),↔(t1(a1,…,an),…, tk(a1,…,an)) 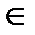 P;
P;
3)  ╞ψ(a1,…,an)∧χ(a1,…,an)
╞ψ(a1,…,an)∧χ(a1,…,an) 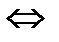
 ╞ψ(a1,…,an) и
╞ψ(a1,…,an) и  ╞χ(a1,…,an);
╞χ(a1,…,an);
4)  ╞ψ(a1,…,an)∨χ(a1,…,an)
╞ψ(a1,…,an)∨χ(a1,…,an) 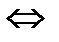
 ╞ψ(a1,…,an) или
╞ψ(a1,…,an) или  ╞χ(a1,…,an);
╞χ(a1,…,an);
5)  ╞ ψ(a1,…,an) → χ(a1,…,an)
╞ ψ(a1,…,an) → χ(a1,…,an) 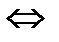 если
если  ╞ ψ(a1,…,an), то
╞ ψ(a1,…,an), то  ╞ χ(a1,…,an);
╞ χ(a1,…,an);
6)  ╞ψ(a1,…,an)
╞ψ(a1,…,an) 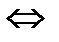 неверно, что
неверно, что  ╞ψ(a1,…,an);
╞ψ(a1,…,an);
7)  ╞
╞  xψ(x,a1,…,an)
xψ(x,a1,…,an) 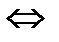
 ╞ψ(a,a1,…,an)длялюбогоа
╞ψ(a,a1,…,an)длялюбогоа 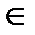 A;
A;
8)  ╞
╞  xψ(x,a1,…,an)
xψ(x,a1,…,an) 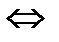
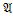 ╞ψ(a,a1,…,an) для некоторого а
╞ψ(a,a1,…,an) для некоторого а 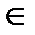 А.
А.
Если не выполняется  ╞φ(a1,…,an), то будем говорить, что формула φ(a1,…,an)ложна в системе
╞φ(a1,…,an), то будем говорить, что формула φ(a1,…,an)ложна в системе  .
.
Пример 1.
Записать формулу φ(x), истинную в 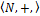 тогда и только тогда, когда х четно.
тогда и только тогда, когда х четно.
Решение.
φ(x)=  y(x=y+y).
y(x=y+y).
Пример 2.
Записать формулу φ'(x,y,z), истинную в 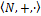 тогда и только тогда, когда z‑наименьшее общее кратное чисел х и y.
тогда и только тогда, когда z‑наименьшее общее кратное чисел х и y.
Решение.
φ'(x,y,z)=ψ(x,y,z)∧χ(x,y,z),где формула ψ «говорит» о том, что z делится на xи на y, а формула χ "говорит"о том, что zделит все общие кратные х и у, т. е. является наименьшим из всех общих кратных:
ψ=  u,∨(z=u∙x∧z=∨х∙y),
u,∨(z=u∙x∧z=∨х∙y),
χ=  w(
w(  u,∨(w=u∙x∧w=∨х∙y)→
u,∨(w=u∙x∧w=∨х∙y)→  w1(w=w1∙z)).Итак,
w1(w=w1∙z)).Итак,
φ'(х,у,z)=  u,∨(z=u∙x∧z=х∙y)∧
u,∨(z=u∙x∧z=х∙y)∧  w(
w(  u,∨(w=ux∧w=хy)→
u,∨(w=ux∧w=хy)→  w1(w=w1z)).
w1(w=w1z)).
Логическое следствие в ЛП
Через  обозначим кортеж переменных
обозначим кортеж переменных 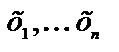 ; через
; через 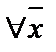 ‑
‑ 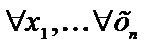 .
.
Определение. Пусть φ1(  ),…,φn(
),…,φn(  ), ψ(
), ψ(  )– формулы сигнатуры ∑. Формула ψназывается логическим следствием формул φ1,…,φn (обозначается φ1,…,φn╞ ψ), если для любой алгебраической системы
)– формулы сигнатуры ∑. Формула ψназывается логическим следствием формул φ1,…,φn (обозначается φ1,…,φn╞ ψ), если для любой алгебраической системы  сигнатуры ∑
сигнатуры ∑
 ╞
╞ 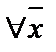 ( φ1(
( φ1(  )
)  …
…  φn(
φn(  )→ψ(
)→ψ(  )).
)).
Пример 1.
Доказать, что φ1(  )→φ2(
)→φ2(  ),φ2(
),φ2(  )→φ3(
)→φ3(  )╞φ1(
)╞φ1(  )→φ3(
)→φ3(  )(1)
)(1)
гдеφ1(  ),φ2(
),φ2(  ),φ3(
),φ3(  ) – формулы сигнатуры ∑.
) – формулы сигнатуры ∑.
Пусть  =‹А, ∑› ‑ произвольная система сигнатуры ∑. Необходимо указать, что
=‹А, ∑› ‑ произвольная система сигнатуры ∑. Необходимо указать, что  ╞
╞ 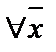 ((φ1(
((φ1(  )→φ2(
)→φ2(  ))
))  ((φ2(
((φ2(  )→φ3(
)→φ3(  ))→(φ1(
))→(φ1(  )→φ3(
)→φ3(  ))).
))).
Пусть 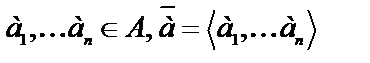 и
и  ╞ ((φ1(
╞ ((φ1( 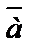 )→φ2(
)→φ2( 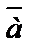 ))
))  ((φ2(
((φ2( 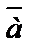 )→φ3(
)→φ3( 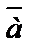 )).
)).
Покажем, что  ╞(φ1(
╞(φ1( 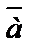 )→φ3(
)→φ3( 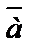 ) (2)
) (2)
Предположим, что  ╞φ1(
╞φ1( 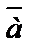 ). Так как
). Так как  ╞(φ1(
╞(φ1( 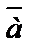 )→φ2(
)→φ2( 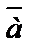 ), то
), то  ╞φ2(
╞φ2( 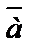 ).
).
Так как  ╞φ2(
╞φ2( 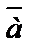 )→φ3(
)→φ3( 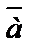 ), то
), то  ╞φ3(
╞φ3( 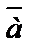 ).
).
Таким образом (2), а, следовательно, и (1), доказано.
Исчисление предикатов
Зафиксируем некоторую произвольную сигнатуру Σ и определим исчисление предикатов сигнатуры Σ (ИПΣ).
Формулами ИПΣбудут формулы сигнатуры Σ.
Примем следующие соглашения. Пусть x1,…,xn‑ переменные, t1,…,tn‑ термы сигнатуры Σ и φ‑ формула сигнатуры Σ. Запись 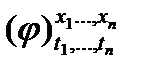 будет обозначать результат подстановки термов t1,…,tnвместо всех свободных вхождений в φпеременных x1,…,xn соответственно, причем, если в тексте встречается запись
будет обозначать результат подстановки термов t1,…,tnвместо всех свободных вхождений в φпеременных x1,…,xn соответственно, причем, если в тексте встречается запись 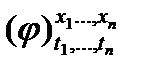 , то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φпеременной xi не входит в подформулу φвида
, то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φпеременной xi не входит в подформулу φвида  y
y 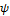 или
или  y
y 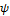 , где у - переменная, входящая в ti.
, где у - переменная, входящая в ti.
Аксиомами ИПΣ являются аксиомы вида 1-10 ИВ, а также аксиомы
11)  xφ→(φ)tx;
xφ→(φ)tx;
12) (φ)tx→ 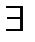 xφ;
xφ;
13)x=x;
14)x=y→((φ)xz→(φ)yz).
Формулы 1-14 называются схемами аксиом ИПΣ.
Правила вывода ИПΣ:
1. φ, φ → ψ ,
ψ
2. ψ →φ ,
ψ→  xφ
xφ
3. φ → ψ ,
 xφ → ψ
xφ → ψ
где в правилах 2 и 3 переменная x не входит свободно в ψ.
Доказательством в ИПΣформулы φназывается такая последовательность φ0,…,φnформул ИПΣ, что φn  φи для каждого i≤n формула φi удовлетворяет одному из следующих условий:
φи для каждого i≤n формула φi удовлетворяет одному из следующих условий:
1) φi‑аксиома ИПΣ;
2) φi получается из некоторых φ1,…, φi-1, по одному из правил вывода 1-3.
Если существует доказательство в ИПΣ формулы φ, то φназывается доказуемой в ИПΣ или теоремой ИПΣ (обозначаем ├φ).
Выводом в ИПΣформулы φ из множества формул φ1,…, φm называется такая последовательность ψ1,…,ψkформул ИПΣ, что φn  φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
1) φi‑аксиома ИПΣ;
2) φi принадлежит Г;
3) φiполучается из некоторых ψ1,…,ψi-1j<i, по одному из правил вывода 1-3, причем при применении правил 2 и 3 переменная х не должна входить ни в одну формулу из Г свободно.
Если существует вывод в ИПΣ формулы φиз множества формул φ1,…, φn, то φназывается выводимой в ИПΣ из Г (обозначаем Г├φ). При этом Г называется множеством гипотез. Очевидно, что доказуемость формулы эквивалентна ее выводимости из пустого множества гипотез. Так же, как в исчислении высказываний, определяется понятие квазивывода. Если Г={ψ1,…,ψn}, то вместо Г├φпишем ψ1,…,ψn├φ.
Формула ψсигнатуры Σ называется тавтологией, если она получается из формулы φисчисления высказываний, доказуемой в исчислении высказываний, путем замены всех ее пропозициональных переменных x1,…,xnна формулы ψ1,…,ψnсигнатуры Σ соответственно. Формулу φпри этом называют основой тавтологии.
Утверждение 1.Любая тавтология φсигнатуры Σ доказуема в ИПΣ.
Следствие 1. Если φи ψ‑ пропозиционально эквивалентные формулы сигнатуры Σ, то φи ψ‑эквивалентные формулы сигнатуры Σ.
В исчислении предикатов ИПΣ справедлива теорема о дедукции.
Теорема 1.(о дедукции).ПустьГ – множество формул ИПΣ,φ,ψ – формулы ИПΣ. Тогда Г,φ├ψ, 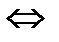 Г├φ→ψ.
Г├φ→ψ.
Эквивалентные формулыИП
Определение эквивалентных формул, утверждения 3,4 при замене формул φ, ψ, χИВ на формулы ИПΣ имеют место.
Утверждение 1.В ИПΣ выполнимы все эквивалентности ИВ из теоремы 5.
Доказательство.Выполнимость в ИПΣ всех эквивалентностей исчисления высказываний следует из следствия 3.
Утверждение 2. В ИПΣ выполнимы следующие эквивалентности, в которых предполагается, что переменная ж не входит свободно в формулу ψ, а переменная у не входит в формулу φ:
1)  xφ≡
xφ≡  xφ,1\)
xφ,1\)  xφ≡
xφ≡  xφ,
xφ,
2)  x(φ∧ψ)≡
x(φ∧ψ)≡  xφ∧ψ, 2\)
xφ∧ψ, 2\)  x(φ∨ψ)≡
x(φ∨ψ)≡  xφ∨ψ
xφ∨ψ
3)  x(φ∧ψ)≡
x(φ∧ψ)≡  xφ∧ψ,3\)
xφ∧ψ,3\)  x(φ∨ψ)≡
x(φ∨ψ)≡  xφ∨ψ,
xφ∨ψ,
4)  xφ≡
xφ≡ 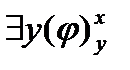 .4\)
.4\)  xφ≡
xφ≡ 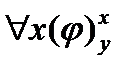
Пример. 1.Докажем эквивалентность а). Построим квазивывод формулы  xφ→
xφ→  xφ из Ø:
xφ из Ø:
1. φ→  xφ‑ аксиома 12;
xφ‑ аксиома 12;
2.  xφ→φ‑ к п.1 применили утверждение 3:
xφ→φ‑ к п.1 применили утверждение 3:
3.  xφ→
xφ→  xφ‑ к п.2 применили правило вывода 2.
xφ‑ к п.2 применили правило вывода 2.
Построим квазивывод формулы  xφ→
xφ→  xφиз Ø:
xφиз Ø:
1.  xφ→φ‑ аксиома 11;
xφ→φ‑ аксиома 11;
2. φ→  xφ‑ к п.1 применили утверждение 3;
xφ‑ к п.1 применили утверждение 3;
3.  xφ→
xφ→  xφ‑ к п. 2 применили правило вывода 3;
xφ‑ к п. 2 применили правило вывода 3;
4.  xφ→
xφ→  xφ‑ к п.З применили утверждение 3.
xφ‑ к п.З применили утверждение 3.
Пример. 2. Докажем эквивалентность г). Построим квазивывод формулы  x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψиз Ø:
xφ∧ψиз Ø:
1.  x(φ∧ψ)→φ∧ψ‑ аксиома 11;
x(φ∧ψ)→φ∧ψ‑ аксиома 11;
2. φ∧ψ→φ‑ утверждение 1;
3.  x(φ∧ψ)→φ‑ к пп.1,2 применили утверждение 1;
x(φ∧ψ)→φ‑ к пп.1,2 применили утверждение 1;
4.  x(φ∧ψ)→
x(φ∧ψ)→  xφ‑ к п.4 применили правило вывода 2;
xφ‑ к п.4 применили правило вывода 2;
5. φ∧ψ→ψ‑ утверждение 1;
6.  x(φ∧ψ)→ψ‑ к пп.1,5 применили утверждение 1;
x(φ∧ψ)→ψ‑ к пп.1,5 применили утверждение 1;
7. (  x(φ∧ψ)→
x(φ∧ψ)→  xφ)→((
xφ)→((  x(φ∧ψ)→ψ)→(
x(φ∧ψ)→ψ)→(  x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψ))‑ аксиома 5;
xφ∧ψ))‑ аксиома 5;
8.  x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψ‑ к пп.4.6.7 применили правило вывода 1.
xφ∧ψ‑ к пп.4.6.7 применили правило вывода 1.
Построим квазивывод формулы  xφ∧ψ →
xφ∧ψ →  x (φ∧ψ) из Ø:
x (φ∧ψ) из Ø:
1.  xφ∧ψ→
xφ∧ψ→  xφ‑ аксиома 3;
xφ‑ аксиома 3;
2.  xφ→φ‑аксиома 11;
xφ→φ‑аксиома 11;
3.  xφ∧ψ→φ‑ к пп.1,2 применили утверждение 1;
xφ∧ψ→φ‑ к пп.1,2 применили утверждение 1;
4.  xφ∧ψ→ψ‑аксиома 4;
xφ∧ψ→ψ‑аксиома 4;
5. (  xφ∧ψ→φ)→((
xφ∧ψ→φ)→((  xφ∧ψ→ψ)→(
xφ∧ψ→ψ)→(  xφ∧ψ→φ∧ψ))‑ аксиома 5;
xφ∧ψ→φ∧ψ))‑ аксиома 5;
6.  xφ∧ψ→φ∧ψ‑ к пп.3,4,5 применили правило вывода 1;
xφ∧ψ→φ∧ψ‑ к пп.3,4,5 применили правило вывода 1;
7.  xφ∧ψ→
xφ∧ψ→  x(φ∧ψ)‑к п.6 применили правило вывода 2.
x(φ∧ψ)‑к п.6 применили правило вывода 2.
Теорема 1. (теорема о замене). Если формула φсигнатуры Σ получается из формулы ψсигнатуры Σ заменой некоторого вхождения подформулы ψ'на формулу φ' сигнатуры Σ и φ'≡ψ', то φ≡ψ.
