Для вероятностей стационарных состояний

В этом параграфе мы познакомимся с одной очень типичной схемой непрерывной марковской цепи – так называемой схемой гибели и размножения, которая понадобится нам для дальнейших исследований. Происхождение этого термина ведет начало от биологических задач, где подобной схемой описываются процессы изменения численности особей в биологических популяциях.

Марковская непрерывная цепь называется процессом гибели и размножения, если все состояния этой цепи можно вытянуть в одну цепочку, в которой каждое из средних состояний связано прямой и

обратной связями с каждым из соседних состояний, а крайние (или крайнее) состояния – только с одним соседним состоянием. Граф состояний такой цепи имеет вид, представленный на рис. 4. Очевидно, что такого рода процесс может описываться как конечной, так и бесконечной цепями Маркова.

Рис. 4

Схема гибели и размножения очень часто встречается, как мы увидим ниже, в самых разнообразных практических задачах теории массового обслуживания. Вследствие этого имеет смысл заранее рассмотреть эту схему в самом общем виде и решить соответствующую систему уравнений Колмогорова для вероятностей равновесных состояний с тем, чтобы в дальнейшем, встречаясь с конкретными процессами, протекающими по такой же схеме, не решать задачу каждый раз заново, а пользоваться уже готовым решением.

Запишем уравнения Колмогорова для вероятностей равновесных состояний. Для нулевого состояния, очевидно, имеем

. (1.5.1)

Для следующего состояния суммы слагаемых, соответствующих входящим и выходящим стрелкам на графе, равны между собой:

,

но в силу соотношения (1.5.1) мы можем сократить здесь справа и слева равные друг другу слагаемые и и тогда, очевидно, получим . Действуя далее аналогичным образом, легко можно найти последовательность формул

;

и так далее, то есть для схемы гибели и размножения слагаемые, соответствующие стоящим друг над другом стрелкам, равны между собой:

, k = 1, 2, … (1.5.2)

Итак, мы нашли, что предельные вероятности p₀, p₁ … в любой схеме гибели и размножения удовлетворяют уравнениям (1.5.2), а также нормировочному условию .

Будем решать полученную систему алгебраических уравнений следующим образом. Из первого уравнения системы выразим p₁ через p₀. Это, очевидно, будет

,

и тогда с учетом последнего соотношения из (1.5.2) получим

. (1.5.3)

Точно так же из третьего уравнения с учетом (1.5.3) следует

и так далее. Теперь в общем виде имеем

, k =1, 2, … (1.5.4)

Легко видеть, что эта формула справедлива для всех значений индекса k, начиная с 1.

Обратим внимание на структуру этого соотношения. В его числителе стоит произведение всех интенсивностей (плотностей вероятностей переходов) 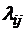, стоящих у стрелок, направленных слева направо, с начала и вплоть до той, которая ведет в k-е состояние системы. В знаменателе – произведение всех интенсивностей , стоящих у стрелок, идущих справа налево, опять-таки с начала и вплоть до той стрелки, которая исходит из k-го состояния на графе состояний.

В случае конечной цепи Маркова для последнего из состояний цепи в числителе будет стоять произведение всех интенсивностей 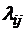, стоящих у всех стрелок, идущих слева направо, а в знаменателе – произведение всех интенсивностей , стоящих у всех стрелок, идущих справа налево.

Итак, сейчас у нас искомые вероятности стационарных состояний p₀, p₁, p₂, … выражены через вероятность p₀ одного из них. Подставим теперь все эти выражения в нормировочное условие и получим

,

откуда сразу же следует

. (1.5.5)

Очевидно, что все остальные вероятности p₁, p₂, p₃, … выражаются через p₀, согласно соотношению (1.5.4), следующим образом:

; ;

Как видим, вероятности предельных состояний найдены, и таким образом задача гибели и размножения в общем виде решена.

* Напомним в этой связи, что полная сумма вероятностей всех событий, исходящих из какой-либо вершины графа, всегда должна быть равной единице, поскольку система обязательно куда-нибудь должна перейти.