Тема 14 Решение квадратного неравенства с опорой на готовый график квадратичной функции
| Теория и практика | |
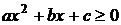 , , 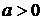 | 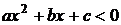 , , 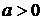 |
Если 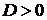 , то , то 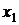 , , 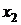 - корни - корни 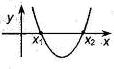 Ответ: Ответ: 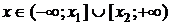 | Если 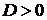 , то , то 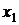 , , 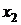 - корни - корни 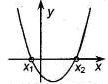 Ответ: Ответ: 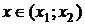 |
Если 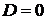 , то , то 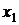 - корень - корень 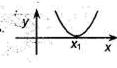 Ответ: Ответ: 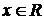 | Если 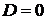 , то , то 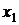 - корень - корень 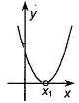 Ответ: Ответ: 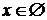 |
Если 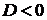 , то корней нет , то корней нет 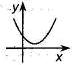 Ответ: Ответ: 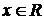 | 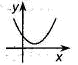 Если Если 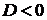 , то корней нет Ответ: , то корней нет Ответ: 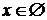 |
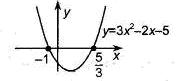 Пример: Пример: 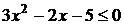 . Рассмотрим . Рассмотрим 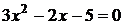 . . 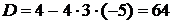 : : 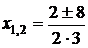 ; ; 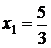 , , 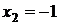 Ответ: Ответ: 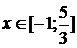 . . |
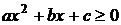 , , 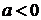 | 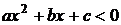 , , 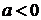 |
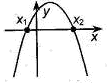 Если Если 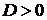 , то , то 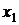 , , 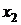 - корни Ответ: - корни Ответ: 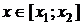 | Если 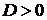 , то , то 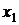 , , 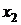 - корни - корни 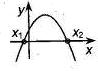 Ответ: Ответ: 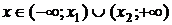 |
Если 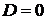 , то , то 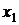 - корень - корень 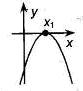 Ответ: Ответ: 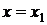 | Если 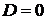 , то , то 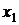 - корень - корень 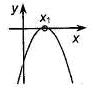 Ответ: Ответ: 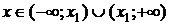 |
Если 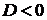 , то корней нет , то корней нет 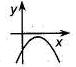 Ответ: Ответ: 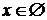 | Если 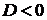 , то корней нет , то корней нет 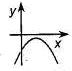 Ответ: Ответ: 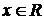 |
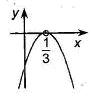 Пример: Пример: 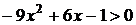 . Рассмотрим . Рассмотрим 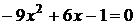 ; ; 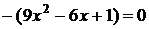 ; ; 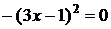 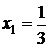 Ответ: Ответ: 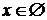 . . |
Реши сам
1. На рисунке изображен график функции 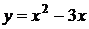 . Используя график, решите неравенство . Используя график, решите неравенство 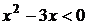 . 1) . 1) 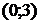 2) 2) 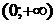 3) 3) 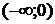 4) 4) 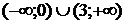 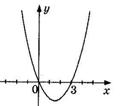 | 2. На рисунке изображен график функции 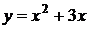 . Используя график, решите неравенство . Используя график, решите неравенство 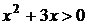 . 1) . 1) 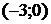 2) 2) 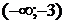 3) 3) 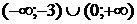 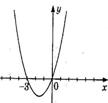 4) 4) 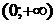 |
3. На рисунке изображен график функции 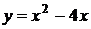 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 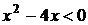 . . 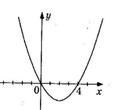 1) 1) 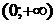 2) 2) 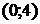 3) 3) 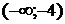 4) 4) 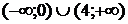 | 4. На рисунке изображен график функции 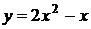 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 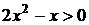 . . 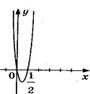 1) 1) 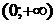 2) 2) 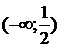 3) 3) 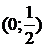 4) 4) 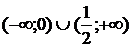 |
5. На рисунке изображен график функции 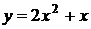 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 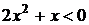 . . 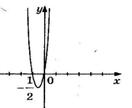 1) 1) 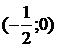 2) 2) 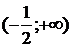 3) 3) 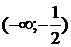 4) 4) 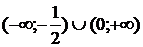 | 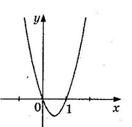 6. На рисунке изображен график функции 6. На рисунке изображен график функции 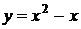 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 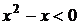 . 1) . 1) 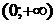 2) 2) 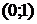 3) 3) 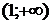 4) 4)  |
7. На рисунке изображен график функции 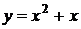 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 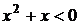 . . 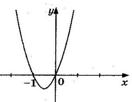 1) 1) 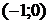 2) 2) 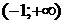 3) 3) 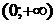 4) 4) 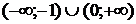 | 8. На рисунке изображен график функции 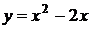 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 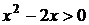 . 1) . 1) 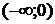 2) 2) 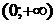 3) 3) 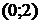 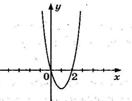 4) 4) 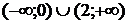 |
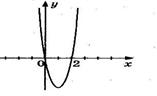 9. На рисунке изображен график функции 9. На рисунке изображен график функции 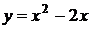 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 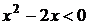 . 1) . 1) 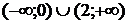 2) 2) 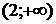 3) 3) 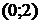 4) 4) 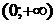 | 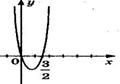 10. На рисунке изображен график функции 10. На рисунке изображен график функции 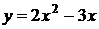 . Используя график, решите графически неравенство . Используя график, решите графически неравенство 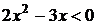 . 1) . 1) 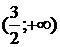 2) 2) 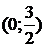 3) 3) 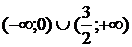 4) 4) 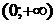 |
Вернуться в содержание
Тема 15 Соотнесение графика квадратичной функции с формулой
Функция вида 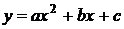 , где
, где 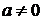 , b, c — числа; x — независимая переменная, называется квадратичной функцией.
, b, c — числа; x — независимая переменная, называется квадратичной функцией.
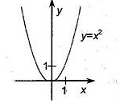 1.
1. 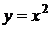
а) О.О.Ф. 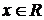 б) О.З.Ф.
б) О.З.Ф. 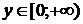
в) нули функции: 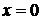 г) Монотонность функции
г) Монотонность функции
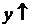 , если
, если 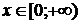
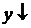 , если
, если 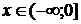
д) ось симметрии — ось ординат
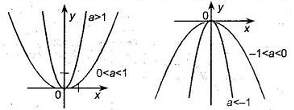 2.
2. 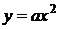
Коэффициент а отвечает за сужение параболы вдоль оси ординат;
если 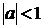 , то ветви расположены дальше от OY; если
, то ветви расположены дальше от OY; если 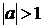 , то ветви расположены ближе к OY.
, то ветви расположены ближе к OY.
3. 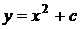
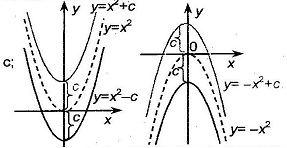 Коэффициент с отвечает за перемещение параболы вдоль оси ординат;
Коэффициент с отвечает за перемещение параболы вдоль оси ординат;
если 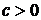 , то график
, то график 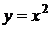 поднимается вверх на с;
поднимается вверх на с;
если 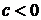 , то график
, то график 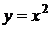 поднимается вверх на с.
поднимается вверх на с.
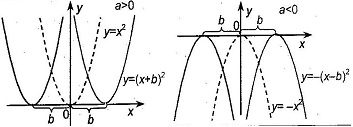 4.
4. 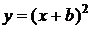
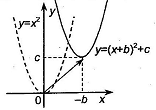
Коэффициент b отвечает за перемещение вдоль оси OX; если 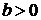 , то влево на b единиц от 0; если
, то влево на b единиц от 0; если 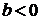 то вправо на b единиц от 0.
то вправо на b единиц от 0.
 |
5.
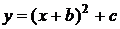
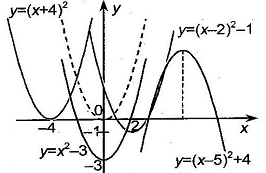
Пример:
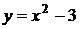
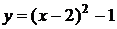
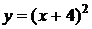
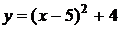
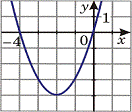
Реши сам: 1. (Демо 2010 задание 15) График какой из перечисленных ниже функций изображен на рисунке? График какой из перечисленных ниже функций изображен на рисунке?
 1)
1) 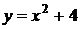
2) 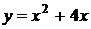
3) 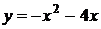
4) 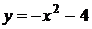
2. График какой квадратичной функции изображен на графике? 1) 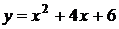 2) 2) 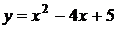 3) 3) 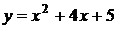 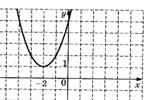 4) 4) 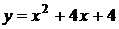 | 3. График какой квадратичной функции изображен на графике? 1) 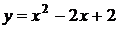 2) 2) 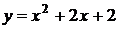 3) 3) 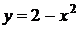 4) 4) 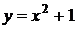 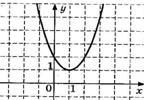 |
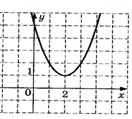 4. График какой квадратичной функции изображен на графике? 1) 4. График какой квадратичной функции изображен на графике? 1) 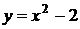 2) 2) 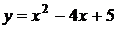 3) 3) 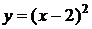 4) 4) 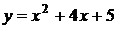 | 5. График какой квадратичной функции изображен на графике? 1) 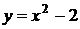 2) 2) 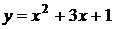 3) 3) 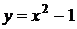 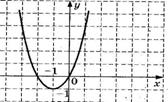 4) 4) 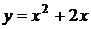 |
6. График какой квадратичной функции изображен на графике? 1) 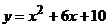 2) 2) 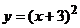  3) 3) 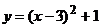 4) 4) 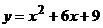 | 7. График какой квадратичной функции изображен на графике? 1) 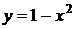 2) 2) 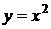 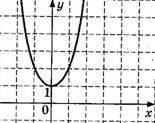 3) 3) 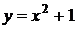 4) 4) 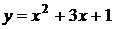 |
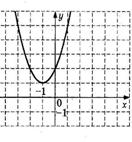 8. График какой квадратичной функции изображен на графике? 1) 8. График какой квадратичной функции изображен на графике? 1) 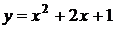 2) 2) 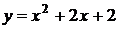 3) 3) 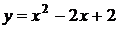 4) 4) 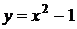 | 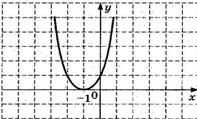 9. График какой квадратичной функции изображен на графике? 1) 9. График какой квадратичной функции изображен на графике? 1) 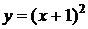 2) 2) 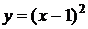 3) 3) 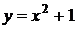 4) 4) 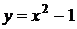 |
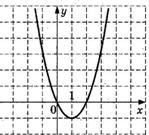 10. График какой квадратичной функции изображен на графике? 1) 10. График какой квадратичной функции изображен на графике? 1) 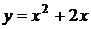 2) 2) 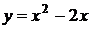 3) 3) 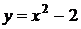 4) 4) 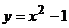 | 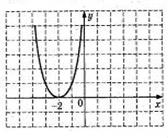 11. График какой квадратичной функции изображен на графике? 1) 11. График какой квадратичной функции изображен на графике? 1) 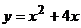 . 2) . 2) 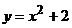 3) 3) 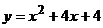 4) 4) 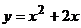 |
Вернуться в содержание
