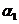Устойчивость линейных систем

7.1. Общие сведения об устойчивости линейных систем

Центральной задачей при исследовании и проектировании систем автоматического регулирования является проверка и обеспечение их устойчивости. Устойчивость является необходимым условием работоспособности систем. Известно, что в процессе работы на систему действуют различные воздействия, вызывая отклонения регулируемой величины от заданного закона движения.

Если под влиянием внешнего воздействия система отклонилась от состояния равновесия или от заданного закона движения и после снятия воздействия вновь возвращается к исходному состоянию или движению, то движение в системе и сама система являются устойчивыми.

Если под влиянием внешнего воздействия система, будучи отклонена от состояния равновесия или от заданного закона движения, после снятия воздействия не возвращается к исходному состоянию или движению и при этом удаление системы от первоначального состояния или закона движения неограниченно возрастает, то движение в системе и сама система являются неустойчивыми.

Рассмотрим дифференциальное уравнение движения линеаризованной системы автоматического регулирования , записанное для регулируемой величины при наличии управляющего воздействия и при равенстве нулю возмущающих воздействий:

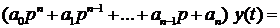
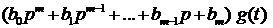= (1.100)

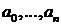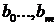Коэффициенты и представляют собой постоянные величины, а оператор .

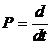Процесс регулирования (движения системы) определяется решением уравнения (1.100), которое представляет собой сумму частного и общего решений:

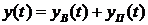
Частное решение 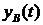соответствует решению уравнения (1.100) с правой частью, а общее решение 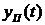, ( которое также называют и переходной составляющей ) соответствует решению этого же уравнения при воздействии 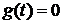. Следовательно, для получения общего решения уравнение (1.72) следует записать в виде:

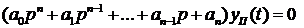. (1.101)

Система будет называться устойчивой, если с течением времени

(t → ∞) переходная составляющая будет стремиться к нулю, 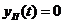. Для нахождения переходной составляющей необходимо решить уравнение (1.101). Это решение известно и может быть записано в вид

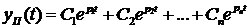(1.102) где: р₁, р₂, . . . , р_n − корни характеристического уравнения

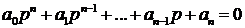; (1.103) C₁, C₂, . . . , C_n − постоянные интегрирования, определяемые из начальных условий.

Необходимо отметить, что в выражениях (1.102) и (1.103) символ « р » не выполняет функцию оператора дифференцирования, а является корнем (решением) характеристического уравнения и представляет собой некоторое комплексное число. Количество корней характеристического уравнения соответствуют его степени 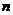, а их содержание определяется только видом левой части уравнения (1.100). Постоянные интегрирования определяются из начальных условий и поэтому зависят от правой части уравнения (1.100). Поэтому быстрота затухания и форма переходной составляющей (переходного процесса) определяется как правой, так и левой частями дифференциального уравнения (1.100). Однако, поскольку в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса, то устойчивость линейной системы не зависит от правой части уравнения (1.100) и определяется только характеристическим уравнением (1.101).

В общем случае корни могут быть вещественными, комплексными и чисто мнимыми. Рассмотрим эти случаи.

1. Вещественный корень. Пусть один из корней, например 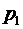, является вещественным 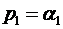, тогда первое слагаемое в выражении (1.102) представляет собой экспоненту 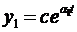. Если 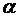₁ < 0, то переходная составляющая при t → ∞ будет затухать. Если α₁ > 0, то составляющая при 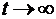будет неограниченно увеличиваться, рис.1.44,а.

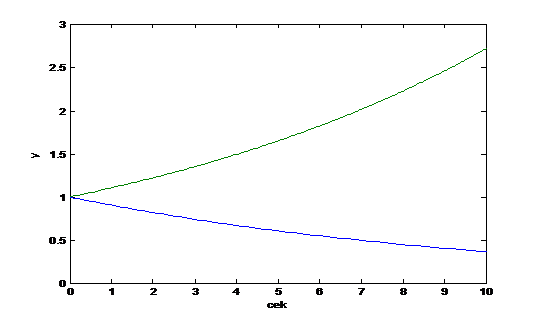
Рис.1.44,а. Переходные составляющая

2. Комплексные корни. Эти корни всегда попарно сопряженные. При отрицательной вещественной части сопряженные корн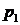и и 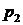будут иметь вид 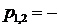α ± jβ. В этом случае слагаемое, определяемое этими корнями в уравнении (1.102), может быть представлено в виде

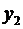= С₁e ^{– (α + jβ)t} + C₂e ^{– (α – jβ)t} = Ae ^–αt sin (βt + ψ), (1.104)

где: А и ψ новые постоянные интегрирования. Видно, что в данном случае 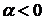переходная составляющая представляет собой затухающие колебания. Причем, мнимая часть корня β определяет частоту затухающих колебаний, а вещественная часть корня α − показатель затухания, определяет затухание огибающей кривой переходного процесса. При положительной вещественной части 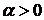колебания переходной составляющей будут расходящимися, рис.1.44,б.

3. Мнимые корни. В этом случае 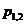= ± jβ. Слагаемое, определяемое этими корнями в выражении (1.3) будет представлять собой незатухающие колебания с постоянной амплитудой А и частотой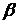

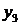= C₁e ^jβt + C₂e ^–jβt = A sin (βt +ψ).

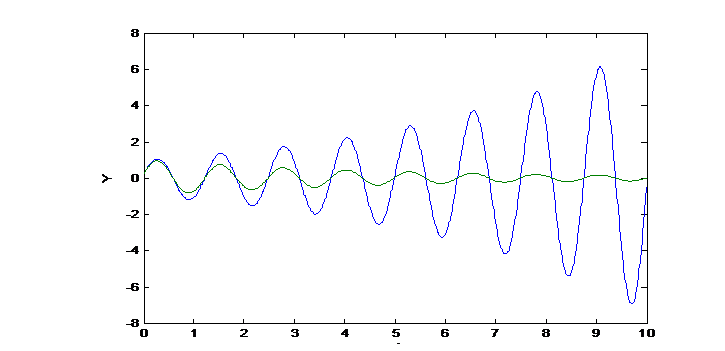
Рис.144,б. Переходные составляющие

Таким образом, для затухания переходного процесса необходимо, чтобы вещественные части корней характеристического уравнения были отрицательными. Если хотя бы один корень характеристического уравнения будет иметь положительную вещественную часть, то весь переходный процесс будет расходиться. Система, имеющая такой переходный процесс, является неустойчивой.

Корни характеристического уравнения можно расположить в виде точек на комплексной плоскости ( рис.1.45)и сформулировать необходимые и достаточные условия устойчивости линейных систем.

Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости расположения корней уравнения. Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой.

Таким образом, мнимая ось представляет собой граничную линию. За эту линию не должны переходить корни характеристического уравнения. Вся левая полуплоскость представляет собой область устойчивости

P=+α1 pP1=.+

P1=-.5

α >0

Превращение устойчивой системы в неустойчивую систему произойдет, когда хотя бы один вещественный или пара комплексных корней перейдет из левой полуплоскости в правую. Граница перехода называется границей устойчивости системы, Рис.1.45.

Y

в)

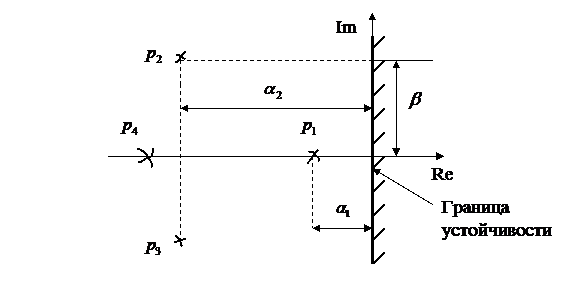
Рис.145. Комплексная плоскость расположения корней

характеристического уравнения

Известно, что ни одна система автоматического регулирования не является строго линейной. Линейные характеристики звеньев и линейные уравнения получаются в результате линеаризации реальных нелинейных характеристик и уравнений. При разложении в ряд Тейлора удерживаются только линейные члены и отбрасываются члены высших порядков, которые для малых отклонений считались пренебрежимо малыми. Обоснование законности такой линеаризации содержится в теоремах Ляпунова:

1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то реальная система будет также устойчивой, т.е. малые нелинейные члены не могут в этом случае нарушить устойчивость системы.

2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то реальная система будет также неустойчивой, т.е. малые нелинейные члены не могут сделать ее устойчивой.

3. При наличии нулевых и мнимых корней поведение реальной системы не всегда даже качественно определяется ее линеаризованными уравнениями. При этом даже малые нелинейные члены могут коренным образом изменить вид переходного процесса, сделав систему устойчивой или неустойчивой.

Необходимо отметить, что опираться в расчетах на приведенные теоремы можно лишь в тех случаях, когда линеаризация выполняется разложением в ряд Тейлора. Напомним, что при этом должно выполняться условие достаточной малости динамических отклонений переменных от их установившихся

значений. К сильно выраженным нелинейностям на больших участках, в том числе и к нелинейностям релейного типа эти теоремы неприменимы.

Из представленного материала следует, что для оценки устойчивости систем необходимо вычислять корни характеристического уравнения. Такие вычисления часто сопряжены с большими, порой не преодолимыми трудностями. Поэтому в тории управления разработаны критерии устойчивости, с помощью которых можно судить об устойчивости системы без вычисления корней характеристического уравнения.

7.2 Критерий устойчивости Гурвица

Необходимые и достаточные условия устойчивости системы любого порядка без решения характеристического уравнения, но с введением в рассмотрение его коэффициентов, были сформулированы Гурвицем в 1895 году. Для рассмотрения этих условий необходимо составить квадратную матрицу коэффициентов, содержащую строк и столбцов (1.105). При составлении матрицы, слева направо по диагонали выписываются коэффициенты характеристического уравнения (1.103), начиная с 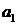и далее в порядке нарастания индекса до коэффициента 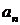включительно. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами.

а₁ а₃ а₅ . . . 0 0

а₀ а₂ а₄ . . . 0 0 .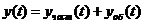

0 а₁ а₃ . . . 0 0
0 а₀ а₂ . . . 0 0 (1.105) . . . . . . . . . . . . …

0 0 0 . . .a_n-1 0

0 0 0 . . .a_n-2 a

В соответствии с критерием Гурвица для выполнения условий устойчивости необходимо и достаточно, чтобы:

1. Все коэффициенты характеристического уравнения были больше нуля;

2.Должны быть больше нуля все 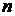определителей Гурвица, составленных из квадратной матрицы коэффициентов (1.105).

Определители составляются по следующему правилу:

∆₁ = а₁ > 0, ∆₂ = а₁а₂ – а₀а₃, (1.106)

∆₃ = а₁а₂а₃ + а₀а₁а₅ – а₁²а₄ –а₀а₃², … Последний определитель включает в себя всю матрицу. Но, так как в последнем столбце матрицы все элементы (кроме последнего элемента) равны нулю, то последний определитель выражается через предпоследний определитель следующей формулой

∆_n = a_n ∆_n-1 > 0. (1.107)

Если предпоследний определитель больше нуля, то условие положительности последнего определителя сводится к условию а_n > 0.

Пример. Уравнение четвертого порядка

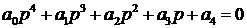
Матрица Гурвица для случая 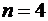имеет вид

а₁ а₃ 0 0

а₀ а₂ а₄ 0 (1.108) 0 а₁ а₃ 0

0 а₀ а₂ а₄

Определители ∆₁ и ∆₂ определяются по формулам (1.106). Выражение для определителя ∆₃ составляется по матрице (1.108), ∆₃= а₁а₂а₃ – а₁²а₄ – а₀а₃². И далее по формуле (1.107) определяется выражение для последнего определителя ∆₄ = а₄ ∆₃. При высоких порядках характеристического уравнения ( 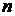>4) применение критерия Гурвица сопряжено с большим объемом вычислительной работы. В этих случаях целесообразно применять другие критерии.

7.3. Критерий устойчивости Михайлова

Критерий устойчивости Михайлова принадлежит к числу частотных критериев и позволяет оценивать устойчивость замкнутой системы по виду годографа, который может быть получен из характеристического уравнения.

Рассмотрим левую часть уравнения (1.72), которая представляет собой характеристический полином:

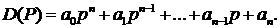(1.109)

Подставим в этот полином чисто мнимое значение р = jω, где ω – угловая частота колебаний, соответствующих чисто мнимому корню характеристического уравнения. В результате получим уравнение кривой Михайлова D(jω) = 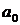(jω)ⁿ + 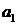(jω)^n-1 +…+ 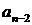(jω)² 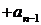(jω) + 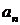. (1.110) Видно, что выражение (1.110) является комплексным, следовательно, его можно расчленить на вещественную и мнимую части U(ω) и V(ω):

U(ω) = 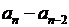ω² 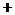…, (1.111)

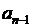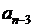V(ω) = ω - ω³ …

Если коэффициенты характеристического полинома (1.109) заданы и задано некоторое значение частоты ω=ω₁, то величина D(jω₁) изобразится на комплексной плоскости в виде точки с координатами U(ω₁) и V(ω₁) или вектора, соединяющего эту точку с началом координат. Если же значение частоты изменять непрерывно от нуля до бесконечности, то вектор D(j 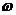) будет изменяться по величине и направлению, описывая своим концом некоторую кривую (годограф), которая называется кривой Михайлова, рис.1.40. Практически кривая Михайлова строится по точкам. Для этого задаются различные значения частоты ω и по формулам (1.111) вычисляются U(ω) и V(ω). Результаты размещаются в таблице и далее строится кривая. Видно, что расчеты и построение кривой Михайлова можно автоматизировать с помощью современных вычислительных средств.

Рис.1.46. Кривая Михайлова

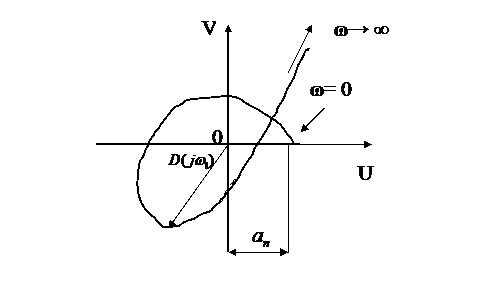
Критерий устойчивости сформулирован А.В.Михайловым в 1936 году. Преимуществом критерия является возможность применения его для оценки устойчивости линейных систем любого порядка.

Формулировка критерия. Для устойчивости системы 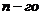порядка необходимо и достаточно, чтобы вектор D(jω), описывающий кривую Михайлова, при изменении ω от нуля до бесконечности имел угол поворота ψ= .

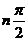Если сформулированные в критерии условия нарушаются, то система автоматического регулирования становится неустойчивой. Признаками неустойчивости могут быть следующие случаи:

кривая Михайлова начинается не на положительной части действительной оси;

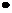нарушен порядок прохождения квадрантов вектором D(jω);

кривая Михайлова проходит через начало координат (это означает, что в характеристическом уравнении имеются мнимые корни и система находится на границе устойчивости).

7.4. Критерий устойчивости Найквиста

Критерий устойчивости Найквиста также относится к числу частотных критериев и позволяет определять устойчивость системы автоматического регулирования (т.е. замкнутой системы) по конфигурации амплитудно- фазовой частотной характеристики, построенной для разомкнутой системы.

Формулировка критерия. Система автоматического регулирования будет устойчивой, если амплитудно-фазовая частотная характеристика

разомкнутой системы не охватывает точку с координатами (-1,0) на комплексной плоскости. Если АФЧХ охватывает точку с координатами (-1,0 ), то система автоматического регулирования оказывается неустойчивой.

Достоинством критерия является возможность использования экспериментально полученных амплитудно – фазовых характеристик для определения устойчивости систем автоматического регулирования. Это необходимо в тех случаях, когда отсутствуют достоверные математические описания объекта управления.

Для выполнения эксперимента необходимо разомкнуть систему и получить данные для построения АФЧХ

На рис.1.47 в системе координат U(ω), V(ω) изображены две амплитудно-фазовые частотные характеристики. Одна из них не охватывает точку с координатами ( -1, j0 ) и поэтому соответствует устойчивой системе. Другая характеристика охватывает эту точку и соответствует неустойчивой системе. Если амплитудно-фазовая характеристика проходит через точку с указанными координатами, то система находится на границе устойчивости.

Рис1.47. Амплитудно - фазовые частотные характеристики

7.5. Построение области устойчивости

При расчете и проектировании САР необходимо обеспечить требуемые показатели качества процессу регулирования. К таким показателям, кроме устойчивости, относятся: колебательность, время переходного процесса, точность в установившемся режиме и др. Количественно показатели качества регулирования, как и устойчивость, зависят от численных значений параметров элементов системы, образующих коэффициенты характеристического уравнения 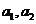и т.д. При этом не каждая устойчивая САР удовлетворяет требованиям, предъявляемым к процессу регулирования. В связи с этим возникает задача поиска значений параметров элементов системы, обеспечивающих требуемое качество регулирования. Для решения этой задачи применяется область устойчивости, которая представляет собой графическое изображение границ областей значений параметров, при которых система оказывается устойчивой.

Построение области устойчивости обычно выполняют в плоскости двух параметров, причем в качестве таковых целесообразно использовать параметры, легко поддающиеся настройке. Такими параметрами могут быть коэффициент усиления, коэффициент передачи и постоянная времени корректирующего элемента. При построении области устойчивости необходимо помнить, что параметры элементов системы могут принимать только положительные значения.

Уравнения границ области устойчивости получаются из определителей Гурвица, если их приравнять к нулю.

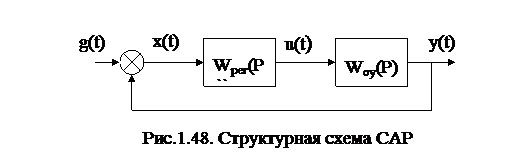
Для иллюстрации построим область устойчивости для системы, структурная схема которой изображена на рис.1.48.

Передаточные функции регулятора и объекта управления соответствуют интегрирующему и апериодическому звеньям:

передаточная функция регулятора ;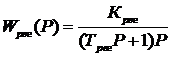

передаточная функция объекта управления 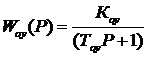; передаточная функция разомкнутой системы

.

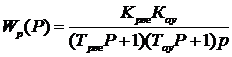Данные для расчета: 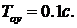, 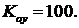Характеристическое уравнение системы имеет вид 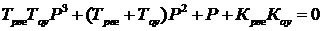. Для получения уравнений границ области устойчивости используем определители Гурвица ∆₁= а₁ =0, ∆₂ = а₁а₂ – а₀а₃ = 0, ∆₃ = а₃∆_2.. С учетом коэффициентов характеристического уравнения определители приобретают вид: ∆₁ = 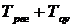, ∆₂ = 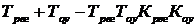, ∆₃ = ∆₂ .

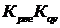Предположим, что требуется построить область устойчивости в плоскости двух параметров: постоянной времени регулятора 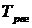и коэффициента передачи регулятора 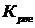.Первый определитель не может участвовать в построении области устойчивости, так как при ∆₁=0, 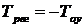. Ранее указывалось, что параметры элементов не могут принимать отрицательных значений. Выражение для второго определителя позволяет получить уравнение границы области устойчивости. Приравнивая определитель к нулю, после несложных преобразований с учетом принятых выше данных получим

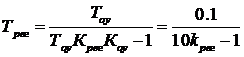(1.112)

Третий определитель не дает дополнительных уравнений для построения области устойчивости.

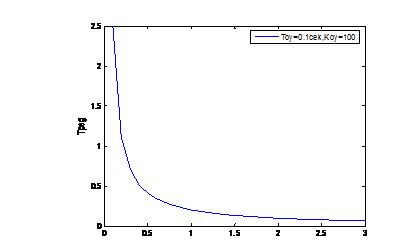
На рис.1.49 изображена кривая, построенная по выражению (1.112). Эта кривая делит плоскость на две части, одна из которых является областью устойчивости. Для определения расположения области устойчивости необходимо сделать пробные расчеты определителей Гурвица для точек, расположенных справа и слева от кривой. В области устойчивости определители должны быть больше нуля. На рис.1.49 область устойчивости расположена слева от кривой. Слева область ограничена асимптотой 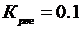(на рисунке не показана), нижней границей является ось абсцисс .

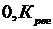Рис.1.49. Область устойчивости