Уравнения систем автоматического регулирования

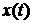При изучении динамических свойств систем автоматического регулирования обычно используются два уравнения: уравнение движения и уравнение ошибки. Первое уравнение описывает движение регулируемой величины , а второе - ошибки регулирования в переходных режимах.

Для получения уравнений рассмотрим два способа. Первый способ предполагает использование передаточных функции системы, второй способ основан на преобразовании структурных схем.

6.1 Передаточные функции системы

Рассмотрим рис.1.39 , на котором изображена система автоматического регулирования. Обозначим передаточную функцию регулятора , передаточную функцию объекта управления . Предположим, что обратная связь в системе разомкнута. Для этого случая можем записать: и .

Далее можно передаточную функцию разомкнутой системы

, (1.78)

где

. (1.79)

Теперь замкнем систему и запишем уравнение замыкания (или уравнение сравнивающего устройства)

. (1.80)

Решая совместно уравнения (1.78) и (1.80) получим передаточную функцию по управляющему воздействию:

(1.81)

Передаточная функция по управляющему воздействию называют еще и передаточной функцией системы.

Если уравнение (1.80) записать относительно регулируемой величины , тогда совместное решение этого уравнения и уравнения (1.79) позволяет получить передаточную функцию системы по ошибке

(1.82)

Получим еще одну передаточную функцию, определяющую связь между ошибкой регулирования и действующим на систему возмущением . Для этого обратимся к рис. 1.39 . Примем, что = 0. В этом случае регулируемая величина должна также равняться нулю. Однако, действующее возмущение обеспечит не нулевые значения регулируемой величине , которые при этом будут являться ошибкой регулирования . Далее, по структурной схеме можно получить передаточную функцию системы по возмущению

6.2. Получение уравнений САР

Для упрощения задачи зададимся передаточными функциями регулятора и объекта управления

, . (1.83)

Получим передаточную функцию разомкнутой системы. Применим уравнения (1.79) и (1.83):

.

Можно также записать

, (1.84)

где (1.85)

Для получения уравнения движения подставим в выражение (1.81) отношение полиномов (1.84). В результате получим

или

. (1.86)

Далее необходимо в уравнении (1.86) вместо обозначений полиномов записать их содержание (1.85) .

В результате получится уравнение движения (1.87)

Для получения уравнения ошибки в выражении (1.82) также используем отношения полиномов (1.84). В результате получим или

(1.88)

Подставив вместо полиномов их выражения, получим уравнение ошибки

Сравнивая уравнения движения и ошибки, замечаем, что они имеют одинаковые левые и разные правые части уравнений.

Уравнение называется характеристическим. Это уравнение отражает собственные свойства системы.

Полином называется характеристическим. Приравнивание нулю характеристического полинома дает характеристическое уравнение системы:

(1.90)

Полученные уравнения движения(1.87) и ошибки (1.89) составлены для некоторого частного случая. В этих уравнениях характеристический полином имеет старшую производную третьего порядка. Поэтому эти уравнения условно называют уравнениями третьей степени. В работоспособных системах старшая производная правой части уравнений не должна быть больше старшей производной характеристического уравнения.

В общем случае для обозначения коэффициентов уравнений обычно применяются прописные буквы а, в, с, d и др. Уравнение движения в этом случае запишется так

= (1.91)

=

где степени старших производных левой и правой частей уравнения ;

и постоянные коэффициенты.

Вид уравнения ошибки отличается от записи (1.91) только обозначениями коэффициентов.

C учетом принятых обозначений для коэффициентов уравнение движения (1.87) следует записать в виде

. (1.92)

В этом уравнении

Часто для записи уравнений применяют только обозначение старшей производной . В этом случае уравнение (1.87) запишется в виде

. (1.93)

При написании уравнения было принято и , но так как в правой части уравнения (1.87) отсутствуют производные выше первого порядка, то в записи (1.93) коэффициенты и отсутствуют.

6.3. Преобразования структурных схем

Составление уравнений системы автоматического регулирования во многих случаях может быть проще и нагляднее, если для этой цели применять структурные преобразования различных соединений звеньев, образующих систему. Рассмотрим преобразования наиболее часто встречающихся соединений звеньев.

Последовательное соединение звеньев. Такое соединение показано на рис.1.40

Нетрудно показать, что результирующая передаточная функция равна произведению передаточных функций отдельных звеньев:

Параллельное соединение звеньев. Такое соединение звеньев показано на рис.1.41,а.

Так как сигнал на выходе всех звеньев складывается, то результирующая передаточная функция равна сумме всех передаточных функций:

Обратные связи.Такое соединение звеньев изображено на рис.1.41,б. Обратная связь может быть положительной и отрицательной. Если обратная связь положительная, то сигналы и складываются на входе, если связь отрицательная, то сигнал вычитается из сигнала . Для определения результирующей передаточной функции запишем следующие соотношения:

Решая эти уравнения совместно, получим результирующую передаточную функцию

Здесь знак минус относится к положительной обратной связи.

Другие правила структурных преобразований. Если структурная схема оказывается сложной и содержит много перекрестных связей, то с помощью определенных правил преобразования ее можно упростить. Основным принципом преобразований структурных схем является равенство друг другу выходных величин исходной и эквивалентной схем. Рассмотрим эти правила:

1. Перенос узлов с выхода на вход, рис.1.42

Видно, что в результате переноса узла разветвления с входа на выход выходная величина не изменилась.

2. Перенос сумматоров рис.1.43,а

3. Перенос сумматоров с входа на выход рис.1.43,б

Здесь также видно, что исходная и преобразованная схемы эквивалентны, так как формулы для определения выходной величины у них одинаковые.

6.4.Уравнения состояния

Уравнение системы или объекта управления может быть представлено в виде системы дифференциальных уравнений первого порядка в так называемой форме Коши [2].

Пусть уравнение объекта или системы имеет вид

(1.94)

где ;

, .

Введем независимых переменных , называемых переменными состояния и представим уравнение в виде системы дифференциальных уравнений

Эти уравнения полностью характеризуют состояние объекта в любой момент времени и поэтому называются уравнениями состояния. Связь между уравнениями состояния и управляемой величиной устанавливается алгебраическим уравнением

Иногда уравнения состояния записывают в векторно-матричной форме:

(1.95)

где матрица размером , матрицы столбцы.

В общем случае матрица имеет вид

(1.96)

В выборе переменных состояния имеется определенная свобода. Важно, чтобы они были независимыми. Однако целесообразно в качестве переменных состояния использовать управляемую величину и ее производные:

(1.97)

Эту форму можно использовать лишь в случае отсутствия в правой части уравнения (1.94) производных от воздействий и , т.е. когда уравнение имеет вид В этом случае форма записи уравнения получается следующей:

(1.98)

При этом матрицы получаются следующими:

Из (1.97) следует, что . Поэтому в уравнении (1.95)

Запись в виде (1.98) соответствует записи уравнений состояния в так называемой нормальной форме. Существуют и другие формы записи, например, каноническая форма. Для ее реализации необходимо определять корни характеристического полинома.

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл и некоторые из них, например, и могут быть измерены датчиками.

Пример.Пусть уравнение объекта или системы имеет вид

,

Уравнения состояния будут иметь вид

Ранее указывалось, что в качестве переменных состояния выбирается сама управляемая величина и ее производные

С учетом принятых переменных, уравнения состояния, записанные в нормальной форме будут иметь вид

(1.99)

где

= =

Управляемость и наблюдаемость. Объект называется полностью управляемым, если существует такое управляющее воздействие 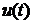, определенное на конечном интервале времени , которое переводит его из любого начального состояния в любое заданное конечное состояние .

Для осуществления такого перехода требуется, чтобы управляющее воздействие прямо или косвенно оказывало влияние на все переменные состояния. В случае нормальной формы записи уравнений состояния объект всегда полностью управляемый. Это видно из уравнений (1.98). Управляющее воздействие входит только в последнее уравнение, прямо влияя только на переменную . Но переменная влияет на переменную , а на и т. д. В результате все переменные оказываются косвенно управляемыми.

Управляемый объект (или автоматическая система) называется полностью наблюдаемым, если все переменные состояния входят в выражение для управляемой величины. Нетрудно убедиться, что при нормальной форме записи уравнений состояния это условие выполняется всегда. При канонической форме записи условие наблюдаемости выполняется только в том случае, когда все коэффициенты в уравнении (1.95) отличны от нуля.

Необходимо отметить, что понятия управляемости и наблюдаемости важны лишь в тех случаях, когда алгоритм управления формируется не в зависимости от ошибки регулирования, а в функции переменных состояния .