Теория автоматического управления является теоретическим обоснованием автоматизации. Отрасль науки и техники, занимающаяся разработкой систем автоматического управления, называется автоматикой.

Первым в мире автоматическим устройством стал автоматический регулятор, изобретенный в 1765г. русским механиком Ползуновым И.И. [1]. Этот регулятор по составу элементов и принципу работы фактически стал первой в мире системой автоматического регулирования. Система предназначалась для регулирования уровня воды в котле паровой машины Ползунова. Принципиальная и структурная схемы системы представлены на рис.1.1 и рис.1.2. В системе объектом управления ОУ

является котел с водой, регулируемой величиной – высота уровня Н. Заданная величина уровня Н_ЗАД устанавливается регулировкой длины стержня, соединяющего двуплечий рычаг с поплавком. Поплавок в системе является чувствительным элементом ЧЭ. Чувствительный элемент измеряет текущее значение уровня - Н и определяет величину отклонения уровня воды в котле ΔН = Н_ЗАД – Н. Функцию регулирующего органа РО выполняет установленная на рычаге заслонка, которая прикрывает доступ воды в котел через патрубок при нежелательном повышении уровня и открывает доступ воды в противном случае. Внешним возмущающим воздействием f, приводящим к снижению уровня в котле, является потребление пара из котла. Обратная связь в регуляторе образована связью между текущим положением уровня жидкости в котле и положением чувствительного элемента. В настоящее время принцип построения систем автоматического регулирования, основанный на измерении отклонения регулируемой величины, называется принципом Ползунова.

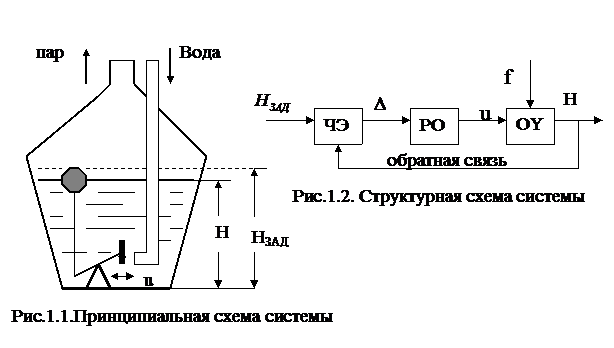
Все системы автоматического регулирования САР разделяются на системы прямого и непрямого действия.

Системой автоматического регулирования прямого действияназывается такая система, в которой воздействие чувствительного элемента на регулирующий орган осуществляется без привлечения дополнительного источника энергии. Только что рассмотренная система регулирования уровня является системой регулирования прямого действия, так как в системе для регулирования используется только энергия чувствительного элемента – поплавка, который при изменении уровня перемещается вверх или в низ.

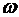Системой регулирования прямого действия является также и система (рис.1.3) автоматического регулирования частоты вращения вала тепловой машины 1. Основу этой системы составляет центробежный регулятор Д . Уатта. Регулирующим органом регулятора является задвижка 6, которая получает перемещение от чувствительного элемента. Чувствительный элемент представляет собой центробежный механизм, состоящий из вращающихся грузов 2, соединенных шарнирными тягами 3 с подвижной втулкой 4. На подвижную втулку с верху в направлении оси У действует сила предварительного сжатия пружины - F_пр. В противоположном направлении действует центробежная сила - F_цб, обусловленная вращением подвижных грузов. Регулируемой величиной является частота (скорость) вращения вала тепловой машины ω. Заданная величина ω_зад в регуляторе устанавливается предварительным поджатием пружины 5. В результате влияния возмущений f(t) регулируемая величина может отличаться от заданной. В этих случаях под действием разности сил ΔF = F_пр - F_цб подвижная втулка 4 переместится в сторону, соответствующую знаку разности 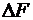и задвижка 6 также изменит свое положение. В результате изменится количество топлива, поступающего в двигатель.

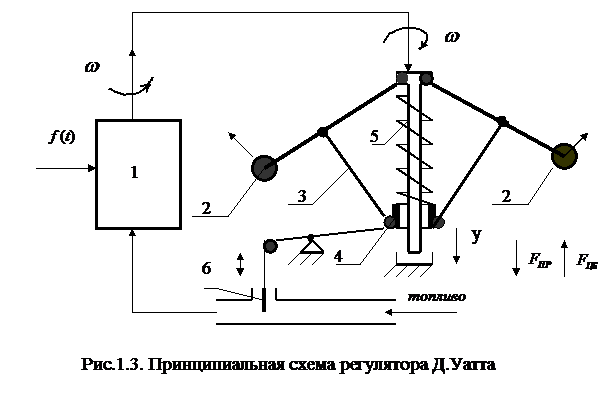
Из материала следует, что регулирующий орган в этой системе, как и в предыдущей системе, приводится в действие энергией чувствительного элемента. Очевидно, что для регулирования чувствительный элемент должен быть достаточно мощным устройством. Если мощности у чувствительного элемента недостаточно, то уменьшается точность регулирования. Например, точность регулирования в рассмотренной системе достигается лишь в том случае, когда чувствительный элемент способен создавать усилия, достаточные для перемещения заслонки 3 и преодоления сил трения, возникающих в подвижных соединениях . Однако во многих случаях мощности чувствительного элемента оказывается недостаточно. В таких случаях между чувствительным элементом и регулирующим органом встраивается усилитель, в результате чего получается система непрямого регулирования.

Системой автоматического регулирования непрямого действия называется такая система, в которой чувствительный элемент воздействует на регулирующий орган не непосредственно, а через специальные усиливающие и преобразующие элементы, питаемые добавочным источником питания.

Примером такой системы может служить система регулирования скорости тепловой машины. На рис.1.4 изображена схема усилительного устройства, которым дополняется предыдущая система прямого действия, изображенная на рис.1.3. В состав устройства входят: гидравлический цилиндр с поршнем 1; управляющий золотник 2; подвижный шток золотника 3.

То

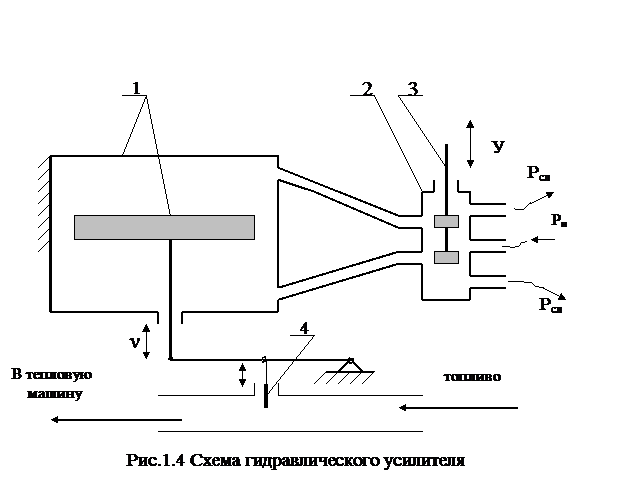
В качестве дополнительного источника энергии используется гидравлическая насосная станция с давлением рабочей жидкости Р_н. Перемещения штока золотника (У) осуществляются в результате движения подвижной втулки 4 центробежного измерителя скорости (рис.1.3). Вследствие малых размеров управляющего золотника, требуются небольшие усилия для перемещения подвижного штока золотника. Сила же давления штока гидравлического усилителя на рычаг заслонки 4 (например, при его движении в низ). определяется величиной рабочего давления Р_н и площадью поршня 1 и поэтому может быть достаточной для перемещения заслонки даже с учетом возможных сил трения.

На рис.1.5 изображена структурная схема рассматриваемой САР. Видно, что в отличие от структурной схемы на рис.1.2 в данную схему системы между чувствительным элементом и регулирующим органом введен дополнительный элемент – усилитель (рис.1.5а).

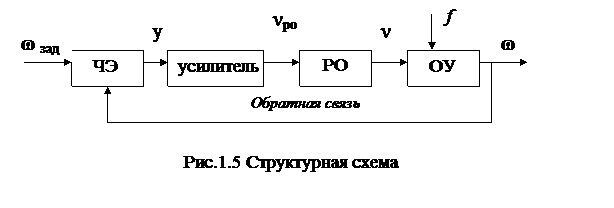
Обратная связь в системе образована функциональной связью между текущей скоростью вращения 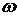с положением подвижной втулки 4, взаимодействующей с пружиной 5. Чувствительным элементом в регуляторе Д.Уатта являются вращающиеся грузы 2 (рис.1.3).

Системы автоматического регулирования разделяют на две группы: системы статические и системы астатические.

Статические системы. Система автоматического регулирования называется статической по отношению к возмущающему воздействию f, если при воздействии, стремящемся с течением времени к некоторому постоянному значению, отклонение регулируемой величины также стремится к постоянному значению, зависящему от величины возмущения.

На рис.1.6,а изображена кривая 1, показывающая изменение отклонения регулируемой величины, после приложения к системе в момент времени t = 0 возмущения f = f₁. На этом же рисунке изображена кривая 2, соответствующая случаю, когда f =f₂. Видно, что величина статической ошибки х_ст зависит от действующего возмущения. На рис.1.6,б приведен пример простейшей системы автоматического регулирования уровня жидкости в емкости. Объектом регулирования в системе является резервуар с жидкостью. Устройство регулирования (регулятор)состоит из поплавка, рычага и задвижки.

Через трубу Т₁ жидкость вливается в емкость, через трубу Т₂ жидкость выливается из емкости. Расход жидкости через трубу Т₂ зависит от потребителя. При равенстве расходов жидкости через трубы Т₁ и Т₂ уровень жидкости в емкости (Н) остается постоянным, что соответствует установившемуся состоянию системы.

В качестве возмущающего и регулирующего воздействий можно рассматривать соответственно расходы жидкости через трубы Т₂ и Т₁.

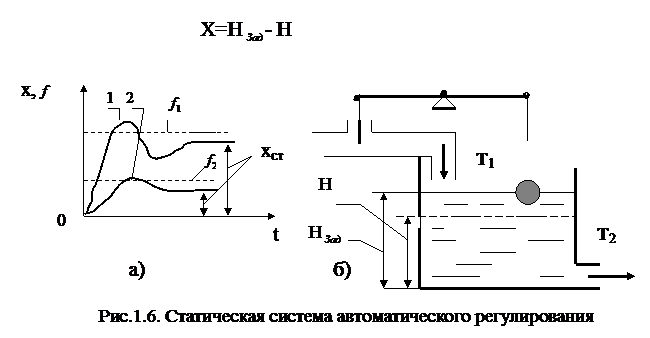
При увеличении расхода жидкости через трубу Т₂ (появилось возмущение) уровень жидкости в емкости понижается, поплавок опускается и переставляет задвижку, увеличивая степень ее открытия. Количество жидкости, поступающей через трубу Т₁ увеличивается и уровень жидкости повышается. Установившееся состояние наступит при равенстве расходов жидкости через обе трубы – Т₁ и Т₂. Однако, этому установившемуся состоянию будет соответствовать другой, пониженный уровень жидкости в емкости - Н₀. Чем больше расход жидкости через трубы Т₁ и Т₂, тем больше открыта задвижка и, следовательно, тем ниже в установившемся состоянии будет уровень жидкости в емкости.

Таким образом, в подобных системах установившееся состояние наступает при различных значениях регулируемой величины, зависящих от действующих возмущений.

Астатические системы.Система автоматического регулирования называется астатической по отношению к возмущающему воздействию, если при воздействии, стремящемся с течением времени к некоторому постоянному значению, отклонение регулируемой величины стремится к нулю вне зависимости от величины воздействия.

На рис.1.7,а изображена кривая, показывающая изменение отклонения регулируемой величины после приложения к системе в момент времени t = 0 возмущения f = f₁. Видно, что с течением времени величина отклонения стремится к нулю.

На рис.1.7,б изображена схема астатической системы регулирования уровня жидкости в емкости. При увеличении или уменьшении расхода жидкости поплавок опускается или поднимается относительно регулируемого уровня - 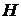. Но в отличие от предыдущей системы рычаг, связанный с поплавком воздействует не на заслонку, а замыкает верхний -1 или нижний -2 контакт обмоток возбуждения 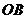. При этом двигатель 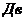начинает вращаться в таком направлении, чтобы выполнить необходимое перемещение задвижки.

Очевидно, что в этой схеме установившееся состояние в системе при любой величине возмущения (изменении расхода через трубу Т₂) может иметь место только при одном определенном значении регулируемой величины, соответствующей нейтральному положению среднего контакта, расположенного на левом конце рычага. При достаточно малом расстоянии между контактами 1 и 2 статическая ошибка в системе будет близка к нулю.

1.2. Принципы управления и определение САР

Существует три основных принципа построения САР, обеспечивающих выполнение требуемого закона изменения регулируемой величины: по разомкнутому циклу, замкнутому циклу и управление по возмущению (принцип компенсации).

Принцип разомкнутого управления.Принцип состоит в том, что алгоритм управления строится только на основе заданного алгоритма функционирования объекта и не контролируется по фактическому значению управляемой величины. Примером реализации данного принципа может служить система управления частотой вращения вала двигателя постоянного тока независимого возбуждения (рис.1.8). При перемещении движка 2 потенциометра 1 изменяется величина напряжения (Un) на входе в усилитель 3. В результате изменяется напряжение в обмотке возбуждения 4 генератора 5, величины тока 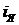в якорной обмотке двигателя 6 и частоты вращения вала двигателя ω. Частота вращения ротора двигателя измеряется с помощью тахогенератора 7 и показывающего прибора 8. Управляющей величиной в данной системе является перемещение движка потенциометра g. Регулируемой величиной является частота вращения вала двигателя. Из схемы следует, что в системе нет замкнутых путей, по которым бы проходил управляющий сигнал. Поэтому система является разомкнутой.

--

Для нормального функционирования систем построенных по принципу разомкнутого цикла необходимо, чтобы они были тщательно отградуированы. Сохранение градуировки обеспечивается жесткостью характеристик элементов, образующих систему. Однако известно, что с течением времени элементы системы изнашиваются, характеристики элементов меняются, и в итоге нарушается градуировка системы. В результате не достигается необходимая точность функционирования объекта и поэтому следует применять другие принципы управления.

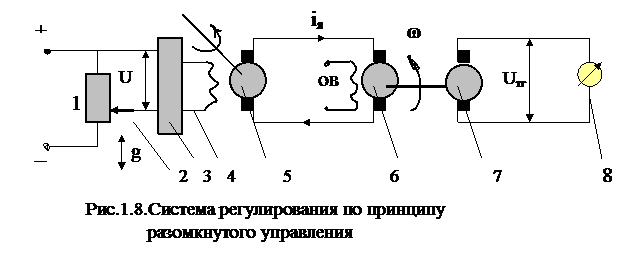
Принцип управления по замкнутому циклу (принцип обратной связи). Принцип основан на измерении отклонения регулируемой величины от предписанного управлением значения с помощью применения обратной связи и элемента сравнения. Образующийся в результате сравнения сигнал отклонения (ошибки регулирования) используется для управления. За счет этого обеспечивается в замкнутых системах требуемый закон изменения регулируемой величины. Примером реализации данного принципа управления может служить система регулирования скорости вращения вала двигателя, изображенная на рис.1.9. Данная система отличается от предыдущей ( рис.1.8) тем, что в ней напряжение, вырабатываемое тахогенератором 7 не направляется на показывающий прибор 8 (рис.1.8), а по обратной связи подается на вход системы (рис.1.9), где сравнивается с напряжением потенциометра U_n. В результате сравнения определяется отклонение регулируемой величины Δu = Un – Uтг. Далее сигнал ошибки регулирования Δu используется для формирования управления. На рис.1.10 представлена структурная схема системы. В схему вошли: измеритель И₁; усилитель (У); исполнительный элемент (ИЭ), в составе генератора с обмоткой возбуждения; объект управления (ОУ) – это двигатель и измеритель (И₂). Кроме указанных элементов в схему вошли устройство сравнения сигналов Un и Uтг и обратная связь.

Измеритель И₁, измеряет величину управляющего воздействия g (величину перемещения движка потенциометра) и преобразует его в сигнал напряжения U_n (управляющая величина). Измеритель И₂, измеряет скорость вращения вала двигателя (регулируемую величину) и преобразует результат измерения также в сигнал напряжения U_тг.

Создание систем управления с разомкнутым принципом работы представляет собой обычно более легкую задачу, чем создание систем с замкнутым циклом работы. Однако, последние обладают рядом несомненных преимуществ. Благодаря своему принципу действия, основанному на измерении ошибки регулирования, системы с замкнутым циклом не требуют точной градуировки и в значительной мере сохраняют свою точность даже и в том случае, когда параметры элементов испытывают существенные изменения во время их работы.

В настоящее время оба принципа управления достаточно широко применяются. Однако, в дальнейшем будет рассматриваться лишь системы , работающие по замкнутому циклу. Такие системы обычно называют системами автоматического регулирования и им можно дать следующее определение:

Системой автоматического регулирования называется система, обладающая свойством сохранять требуемую функциональную связь между управляющими и регулируемыми величинами при помощи их сравнении и использования получающихся при этом разностей для управления.

В случае схемы системы, изображенной на рис.1.9 величинами между которыми необходимо сохранять требуемую функциональную связь являются сигналы U_n и U_тг.

Изменения регулируемых величин вызываются не только управляющими , но и возмущающими воздействиями, приложенными к системе автоматического регулирования

Возмущающим называется всякое воздействие, которое стремится нарушить требуемую функциональную связь между управляющим воздействием и регулируемой переменной.

В случае рассмотренной системы регулирования возмущающим воздействием может быть изменение момента нагрузки, приложенного к валу двигателя, нарушение температурного режима работы обмоток двигателя и др.

Очевидно, что система регулирования по-разному должна вести себя в отношении к указанным двум типам воздействий. Управляющие воздействия должны определять изменения регулируемых переменных, возмущающие же воздействия ,наоборот, должны оказывать как можно меньшее влияние на изменения регулируемых переменных. Указанные воздействия отличаются также и местами их приложения к системе. Если управляющее воздействие может быть приложено к системе только через ее вход (через измеритель), то возмущающее воздействие может быть приложено к любой точке системы.

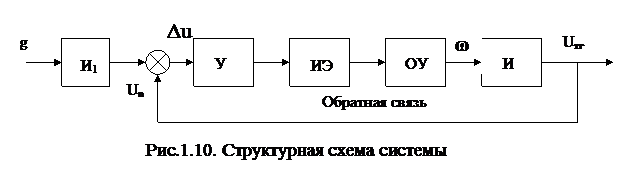
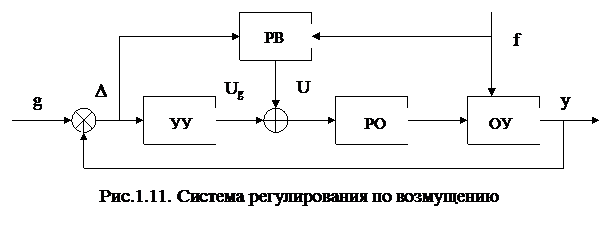
Управление по возмущению (принцип компенсации). Так как отклонение регулируемой величины 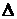зависит не только от управления, но и от возмущающего воздействия f (рис.1.11), то закон управления целесообразно строить так, чтобы в установившемся режиме отклонение 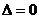. Функциональная схема системы регулирования по возмущению представлена на рис.1.11, где: УУ - управляющее устройство, формирует составляющую управления U_g = F₁( 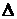); РВ – регулятор по возмущению, формирует составляющую управления U_f = F₂(f, 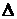); РО – регулирующий орган; ОУ – объект управления.

Для работы регулятора по возмущению необходимо иметь возможность для измерения возмущений, что не всегда оказывается возможным, так как в настоящее время практически отсутствуют такие измерители. Применение вычислительных устройств расширяет возможности для применения регуляторов и выводит этот принцип управления в число перспективных.

в

1.3. Основные элементы и классификация САР.

Любая САР состоит из объекта регулирования и регулятора. Автоматические регуляторы являются достаточно сложными устройствами. Однако, при всей их сложности, регуляторы всегда можно представить устройствами, состоящими из следующих основных элементов, рис.1.12:

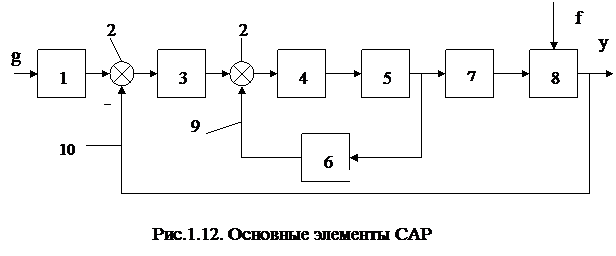
1 - измерительный элемент, предназначен для измерения и преобразования управляющего воздействия в управляющую величину;

2 – устройство сравнения, установленное на входе системы выполняет операцию вычитания из входного сигнала, сигнала обратной связи с целью определения сигнала, соответствующего ошибке регулирования;

3 – последовательно включенный корректирующий элемент, служит для преобразования сигнала ошибки регулирования с целью придания системе требуемых динамических свойств;

4 – усилительный элемент, усиливает сигнал управления;

5 – исполнительный механизм, вырабатывает регулирующее воздействие, прикладываемое к объекту управления. Механизм содержит исполнительный элемент ( как правило, двигатель), промежуточное устройство (редуктор или др. преобразователь) и регулирующий орган непосредственно воздействующий на объект управления;

6 – параллельно включенный корректирующий элемент – для придания системе требуемых динамических свойств;

7 - объект управления;

8 – измерительный элемент, предназначен для измерения и преобразования регулируемой величины в сигнал главной обратной связи, совпадающий по виду энергии с входным сигналом;

9 – дополнительная обратная связь. Может быть гибкой, если корректирующий элемент 6 дифференцирует входной сигнал и жесткой в других случаях;

10 – главная (основная) обратная связь, для организации управления по замкнутому циклу.

Рис. 1.13. Упрощенный вариант изображения структурной схемы САР

При изучении теории управления принято использовать также и упрощенные структурные схемы. Например, на схемах можно не изображать измерительные элементы, если рассматриваемый материал не относится к этим элементам. Более того, на схемах часто регулятор представляется в виде одного звена, если рассматриваемый материал не требует его поэлементного рассмотрения. 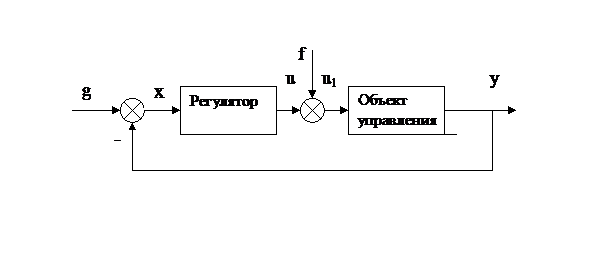После упрощений структурная схема САР принимает следующий вид Приведенные на схеме обозначения сигналов (рис.1.13) в дальнейшем изменяться не будут:

g – управляющее воздействие;

х – отклонение регулируемой величины (ошибка регулирования), определяется с помощью уравнения замыкания х = g – у, которое одновременно является уравнением сравнивающего устройства;

у – регулируемая величина;

u – сигнал управления от регулятора;

f – возмущающее воздействие;

u₁ – сигнал управления, u₁=f – y.

Следует указать, что все приведенные сигналы в общем случае являются функциями времени. В совокупности эти сигналы могут также называться переменными или координатами системы.

Если из схемы системы исключить сигнал управляющего воздействия 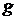, то ее назначение сведется только к парированию вредного влияния действующего возмущения 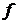. Подобного рода системы принято называть системами автоматической стабилизации, отрабатывающими сигнал возмущения. Если управляющее воздействие постоянно (g=g₀), то такие системы называют системами автоматического регулирования (САР). Если управляющее воздействие непрерывно изменяется, то системы относят к программным (если закон изменения воздействия соответствует некоторой известной программе) или к следящим системам, если этот закон является произвольным.

1.4. Требования к САР

При определении САР указывалось, что эти системы должны иметь свойство сохранять требуемую функциональную зависимость между изменениями управляющего воздействия и изменениями регулируемой величины. Однако, чем точнее поддерживается функциональная связь, тем дороже система. Поэтому очень важно правильно сформулировать требования к САР, которые отличают реальную систему от идеальной системы.

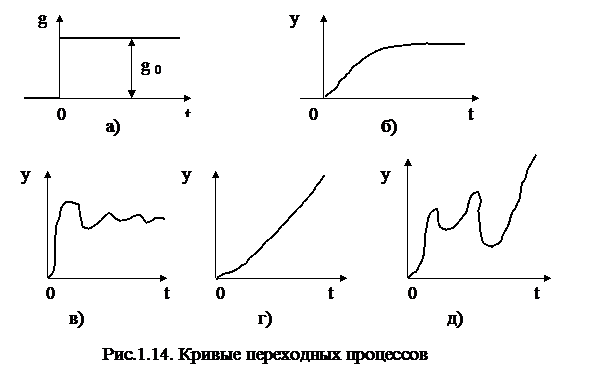
Если на вход системы автоматического регулирования подать управляющий сигнал g(t) = g₀ (рис.1.14,а) и принять f(t) = 0, то на выходе системы возможны следующие виды процессов изменения регулируемой величины у(t):

1. Не колебательный процесс (рис.14,б). Кривая у(t) ограничена по величине и соответствует форме сигнала управляющего воздействия (рис.14,а) после прохождения некоторого отрезка времени, называемого временем переходного процесса. Такого типа процессы соответствуют устойчивым системам;

2. Колебательный процесс (рис.14,в). Кривая у(t) ограничена по величине, и после завершения колебаний соответствует форме сигнала управляющего воздействия. Процесс также соответствует устойчивой системе;

3. Не колебательный процесс (рис.1.14,г). Кривая у(t) не ограничена по величине и не стремится к форме сигнала управляющего воздействия. Процесс соответствует неустойчивой системе. Такие системы не работоспособны;

4. Колебательный процесс (рис.1.14,д). Кривая не ограничена по величине и не стремится к форме сигнала управляющего воздействия, Поэтому данный процесс также соответствует неустойчивой и неработоспособной системе.

Из представленного материала следует, что только устойчивые системы автоматического регулирования работоспособны. Неустойчивость систем обусловлена несовершенством регулятора. Следствием этого является нарушение энергетического баланса в системе. В результате этого по обратной связи на вход системы возвращается слишком много энергии, которая и раскачивает систему. Таким образом, главным требованием, предъявляемым к системам должно быть требование устойчивости САР.

Устойчивые системы обладают свойством, при котором отклонение регулируемой величины от требуемого закона изменения с течением времени стремится к нулю, т.е. х(t) = g(t) – y(t) = 0 (при t→∞). Свойство устойчивости САР обеспечивается подбором значений параметров элементов регулятора (моменты инерции вращающихся тел, постоянные времени корректирующих устройств, и т.д.). В процессе работы с течением времени значения параметров могут изменяться. Система же при этом не должна терять свойства устойчивости. Следовательно, САР должна обладать еще и некоторым запасом устойчивости. Чем он выше, тем больше гарантии устойчивой работы системы.

Не менее важными являются требования, предъявляемые к поведению системы в переходном процессе.

Переходный процесс в системе возникает всегда после приложения к ней внешнего воздействия. При исследовании систем в качестве такого воздействия применяется единичная ступенчатая функция (типовое воздействие – единичный скачек). Обозначается: g(t) = 1(t). Графически единичный скачок изображается так же, как и на рис.1.14,а, только величина воздействия g₀ должна быть равна 1(t).

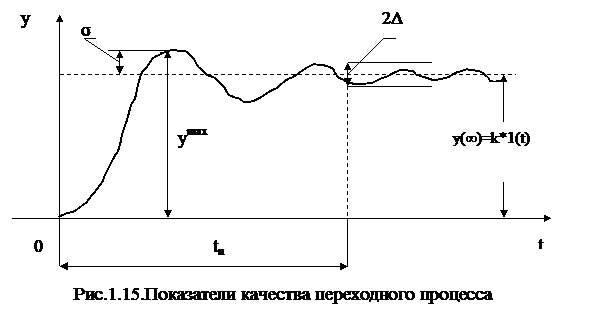
На рис.1.15 изображена кривая изменения регулируемой величины у(t), после приложения к системе типового воздействия. Часть кривой в интервале времени [0, t_n] является переходным процессом. За переходным процессом располагается часть кривой, соответствующей установившемуся режиму в системе. Из рисунка следует, что на установившемся режиме кривая у(t) продолжает изменяться. Однако считается, что этими изменениями можно пренебречь.

Переходный процесс характеризуется следующими показателями качества регулирования:

1.Максимальное отклонение регулируемой величины у^мах. Допустимое значение этого показателя устанавливается заказчиком ;

2. Перерегулирование – σ % = [y^max - y(∞)]*100 / y(∞), где у(∞) – установившееся значение регулируемой величины (при t →∞). Максимальная величина перерегулирования не должна превышать 30%;

3. Время переходного процесса t_n, т.е. время, прошедшее от момента приложения воздействия (t = 0) до момента входа кривой у(t) в трубку переходного процесса размером 2Δ ( Δ =0.01¸0.05) у(∞)). Допустимая величина времени t_n устанавливается заказчиком системы;

4. Количество колебаний регулируемой величины за время переходного процесса. Форма переходного процесса задается – с колебаниями или без них. Если переходный процесс предполагается иметь с колебаниями, то количество колебаний должно быть не больше трех.

Считается, что система автоматического регулирования имеет удовлетворительные (или хорошие) динамические свойства, если ее переходный процесс отвечает перечисленным выше требованиям.

Употребив выражение «динамические свойства» уместно определить термин «динамика». В обучении, динамика – это раздел механики, занимающийся изучением движения тел под действием приложенных к ним сил. В управлении, слово «динамика» можно понимать как движение переменных (координат) системы под влиянием приложенных к ней внешних воздействий, а сочетание слов «динамические свойства» – как инструмент обобщенной оценки качества этого движения. Динамические свойства могут быть удовлетворительными и неудовлетворительными.

Другими важными требованиями к САР являются:

требование к величине ошибок систем автоматической стабилизации при нахождении их в установившемся состоянии (статическая точность)

х_ст= g(t) – y(t)| _t→∞;

требование к динамической точности, применяется для следящих систем и систем с программным управлением х_дин(t) = g(t) – y(t). Уже известно, что в этих системах управляющее воздействие изменяется непрерывно в процессе всей работы. Поэтому статические ошибки для этих систем не характерны. Количественные характеристики требований зависят от типа разрабатываемых систем и указываются в технических заданияx.

1.5. Линейные законы регулирования

Законом регулирования называется зависимость между регулирующим воздействием и отклонением регулируемой величины от заданного значения.

Математически закон регулирования определяется уравнением автоматического регулятора. Для систем автоматического регулирования закон регулирования в простейшем случае записывается в виде

u(t) = f [x(t)].

В общем случае закон регулирования включает в описание не только ошибку регулирования, но и ее производные и интегралы

u(t) = f [ , ,…].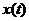

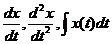На практике используются следующие законы регулирования:

1. Пропорциональный закон регулирования

u(t) = k_p x(t), (1.1)

k_p – параметр настройки регулятора.

Регулятор в этом случае называется П – регулятор.

Исследуем особенности этого закона регулирования. После дифференцирования получим

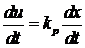. (1.2)

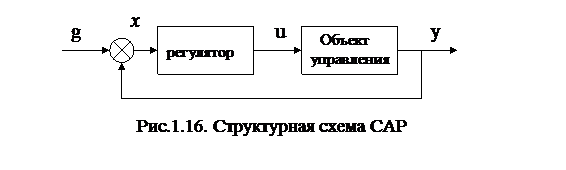
Выясним, характерна ли системе с рассматриваемым законом регулирования статическая ошибка. Уже известно, что статическая ошибка х_ст характеризует точность системы автоматической стабилизации в установившемся режиме. Отметим, что на установившемся режиме сигнал управления от регулятора 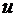(рис.1.16) не изменяется, следовательно, 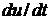=0. Из этого делаем вывод, что в выражении (1.2) скорость 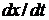также равна нулю. Однако при этом ошибка регулирования может быть отличной от нуля. Это означает, что системе с П – законом регулирования характерна статическая ошибка. Это является недостатком.

Преимуществом закона регулирования является то, что сигнал управления от регулятора возникает одновременно с появлением ошибки регулирования. При этом величина сигнала пропорциональна ошибке. Это способствует уменьшению времени регулирования.

2. Интегральный закон регулирования

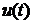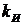
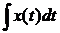= , (1.3)

K_и – параметр настройки регулятора.

Регулятор в этом случае называется И – регулятор.

Выполним дифференцирование выражения (1.3). В результате получим

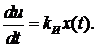(1.4)

На установившемся режиме 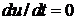. Из выражения (1.4) следует, что в этом случае и ошибка регулирования 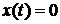. Следовательно, системе регулирования с И – законом регулирования не характерна статическая ошибка. Это свойство повышает точность регулирования и является преимуществом закона регулирования. Однако из выражения (1.3) следует,

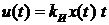. (1.5)

Из выражения (1.5) следует, что в самом начале регулирования при t ≈ 0 и 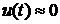, хотя величина ошибки при этом может быть значительной. Это приводит к тому, что процесс регулирования в начальной фазе оказывает несущественное влияние на объект регулирования. При увеличении времени влияние на объект усиливается. Получается, что процесс регулирование как – бы отстает от процесса появления и изменения ошибки. В результате регулирование оказывается растянутым по времени. Процессу регулирования характерны колебания регулируемой величины.

3. Пропорционально – интегральный закон регулирования

u(t) = k_p[x(t) + 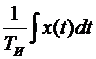], (1.6)

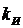- параметр настройки регулятора, .

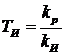Регулятор в этом случае называется ПИ – регулятор.

Применение данного закона регулирования позволяет устранить недостатки и использовать преимущества рассмотренных первых двух законов. В результате получается не длительное регулирование и без статической ошибки на установившемся режиме.

4. Пропорционально – дифференциальный закон регулирования

u(t) = k_p[ 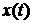+ 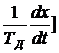, (1.7)

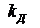- параметр настройки регулятора, .

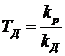Регулятор в этом случае называется ПD – регулятор.

Наличие производной в законе позволяет ввести в процесс регулирования эффект опережения, в результате чего регулятор вступает в работу уже в тот момент времени, когда ошибка регулирования еще равна нулю, т. е. при регулировании улавливается скорость изменения ошибки. Использование этого эффекта позволяет уменьшить время регулирования. Это является преимуществом данного закона регулирования.

5. Пропорционально – интегрально- дифференциальный закон регулирования

u(t) = k_p(x(t) + 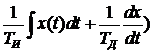. (1.8)

Наличие в законе трех составляющих позволяет добиться высокого качества, как в переходных процессах, так и на установившихся режимах регулирования.

2. Уравнения элементов САР. Получение уравнений

Для получения описаний уравнений элементов используются физические законы, определяющие их поведение в системе. Обычно такими законами являются:

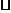второй закон Ньютона в виде

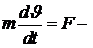для описания прямолинейного движения тела (m – масса, F – движущая сила, 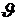- линейная скорость движения ), а также для описания вращательного движения тела в виде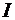 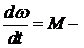( 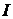- момент инерции вращающейся массы, 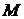- вращающий момент, 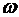- угловая скорость);

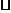закон сохранения энергии в виде

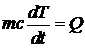- для описания изменения температуры тела 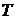c массой 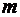и удельной теплоемкостью « 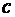» под действием приложенного теплового потока ;

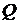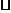уравнение состояние газа в виде 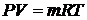- для установления математической связи давления газа 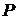, его температуры 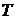и объема 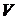физически однородной системы в состоянии термодинамического равновесия (R – газовая постоянная, 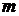- масса газа).

Кроме указанных применяются и другие законы физики, например, устанавливающие связь меж<