Построение рабочей области (к упр.32)
kh=10
koc=0.1:.01:1
ky3=1.11*(1.15+150.*koc).*(1+150.*koc);
ky4=2*kh*(150.*koc+1).^2./(1.15+150*koc)
plot(koc,ky3,koc,ky4);
Проверка расположения рабочей точки в рабочей области
koc=.8
ky=100
a0=.015
a1=150*koc+1.15
a2=150*koc+1
a3=3*ky
po=a3*a1/(.75*a2.^2)
raz1=a0*a2-6*a1^2
raz2=a0^2*a3-a1^3
raz3=a0*a3-.5*a1*a2
raz4=a1*a3-6*a2.^2

Рис. 7.4. Рабочая область
Расчетная формула в третьей строке соответствует границе, обозначенной на рис. 7.4 символом 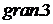 . Расчетная формула в четвертой строке соответствует границе, обозначенной на рис.7.4 символом
. Расчетная формула в четвертой строке соответствует границе, обозначенной на рис.7.4 символом 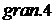 . Следует отметить, что эта кривая не является границей. Она в 10 раз выше действительной кривой. Такое масштабирование выполнено с помощью коэффициента
. Следует отметить, что эта кривая не является границей. Она в 10 раз выше действительной кривой. Такое масштабирование выполнено с помощью коэффициента 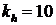 с целью показа рабочей области «
с целью показа рабочей области « 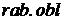 ». Последние четыре строки соответствуют системе неравенств (7.1).
». Последние четыре строки соответствуют системе неравенств (7.1).
Для получения графического материала использованы возможности системы MATLAB.
Задача 46.Передаточная функция разомкнутой системы регулирования
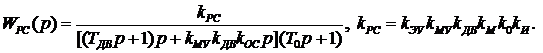
Исходные данные: 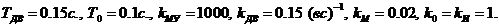 . На рис. 7.5 показана рабочая область системы.
. На рис. 7.5 показана рабочая область системы.
Определить время переходного процесса для рабочих точек с координатами:
1) 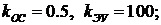 2)
2) 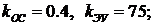 3)
3) 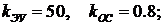
4) 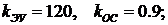 5)
5) 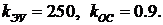
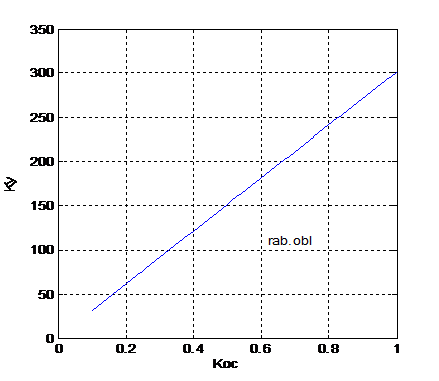
Рис.7.5. Рабочая область (к задаче 46).
Упражнение 33. Разработать алгоритм и составить программу для автоматизации расчета рабочей области в задаче синтеза САР.
Решение. Задачу отнесем к системе, описываемой уравнением третьего порядка
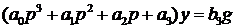 ,
,
где некоторые коэффициенты, например 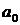 и
и 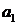 , являются известными числами, а другие коэффициенты
, являются известными числами, а другие коэффициенты 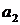 и
и 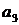 - функциями переменных параметров, например коэффициента усиления
- функциями переменных параметров, например коэффициента усиления 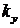 и коэффициента коррекции
и коэффициента коррекции 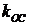 . Пусть
. Пусть 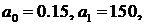
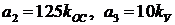 . (7.2)
. (7.2)
Запишем уравнения границ рабочей области (7.1) с учетом функциональных зависимостей (7.2)
1.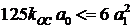 ;
;
2. 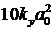 <= 1.05
<= 1.05 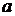 13; (7.3)
13; (7.3)
3. 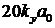 <=
<= 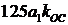 ;
;
4. 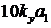 <=
<= 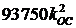 .
.
Напомним, что представленные соотношения являются уравнениями границ только при использовании знака равенства. Знак неравенства позволяет определить направление расположения рабочей области относительно границ, описываемых данными уравнениями.
Для построения рабочей области уравнения границ целесообразно записать относительно неизвестных параметров, например, относительно коэффициента усиления. Однако, из содержания описаний (7.3) следует, что в первом соотношении коэффициент усиления отсутствует, поэтому записать его можно только относительно коэффициента 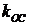 . В результате уравнения границ будут иметь вид:
. В результате уравнения границ будут иметь вид:
для первой границы 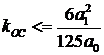 ;
;
для второй границы 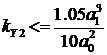 ; (7.4)
; (7.4)
для третьей границы 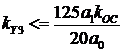 ;
;
для четвертой границы 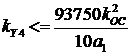 .
.
Подставим в уравнения (7.4) численные значения коэффициентов: 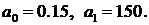 В результате получим:
В результате получим:
для первой границы 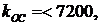
для второй границы 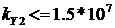 ,
,
для третьей и четвертой границ: 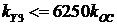 ,
, 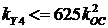 .
.
Видно, что первые два неравенства являются просто ограничениями для переменных параметров 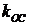 и
и 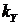 . Третье и четвертое неравенства представляют собой линейную и квадратичную зависимости коэффициента усиления от коэффициента
. Третье и четвертое неравенства представляют собой линейную и квадратичную зависимости коэффициента усиления от коэффициента 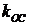 . Эти зависимости в основном и определят конфигурацию рабочей области.
. Эти зависимости в основном и определят конфигурацию рабочей области.
Далее строится рабочая область. Можно в рабочей области построить линию, разделяющую рабочую область на подобласти апериодических и колебательных процессов. Для этого применяется уравнение [2]
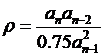 , (7.5)
, (7.5)
где 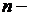 номер старшей производной в характеристическом уравнении.
номер старшей производной в характеристическом уравнении.
Разделительное уравнение получается, если принять 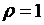 . В этом случае уравнение (7.5) принимает вид
. В этом случае уравнение (7.5) принимает вид
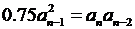 .
.
В данной задаче  . С учетом этого находим
. С учетом этого находим
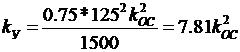 .
.
Расчет рабочей области целесообразно выполнить на ПК с привлечением системы MATLAB и следующей программы.
Программа для расчета и построения границ рабочей области.
1. Задаются численные значения постоянным параметрам
a0=.15;
a1=150;
2.Организуется цикл
Koc =.1:.01:10;
3.Рассчитываются данные для третьей и четвертой границ
ky3=125*a1*Kос/(20*a0);
ky4=9375*Kос^2/a1;
4. Построение разделительной линии ро=1
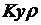 =7.81*Koc^2;
=7.81*Koc^2;
5. Bывод графиков
plot(Koc,ky3,Koc,ky4,Koc,kyp,)
.  .
.
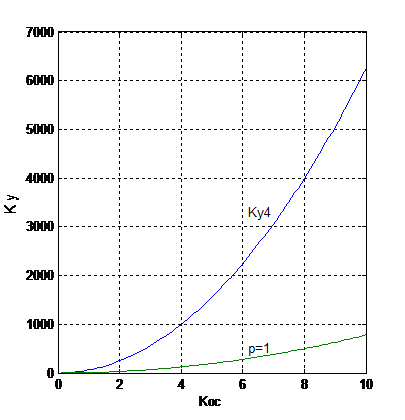
Рис.7.6. К упражнению 33
На рис. 7.6 представлены результаты расчета. Рабочая область простирается вниз от четвертой границы вплоть до оси абсцисс. Граница обозначена символом 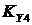 Третья граница (на рисунке не показана) не влияет на очертание рабочей области. В рабочей области проведена разделительная линия
Третья граница (на рисунке не показана) не влияет на очертание рабочей области. В рабочей области проведена разделительная линия 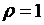 .
.
Задача 47.Для системы, рассмотренной задаче 46, определить расположение в рабочей области (рис.7.5) подобластей апериодических и колебательных процессов.
Упражнение 34. Рабочая область на рис. 7.5. соответствует задаче, рассмотренной в упражнении 32. Используя имеющиеся там данные, нанести на рабочую область линии, соответствующие постоянным значениям времени апериодических переходных процессов 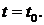
Решение. В соответствие с задачей в упражнении 32 уравнение автоматической системы имеет вид
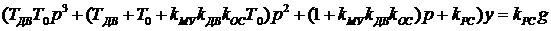
где 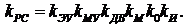
Исходные данные:
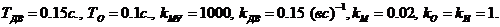
Уравнение системы можно записать, используя общепринятые обозначения коэффициентов
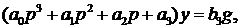
где 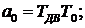
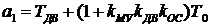 ;
; 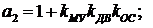
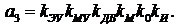
Предварительно выделим подобласть апериодических процессов. Для этого запишем уравнение разделительной линии, Напомним, что уравнение получается из формулы для определения параметра  . При этом разделительная линия получается, если формулу приравнять к единице
. При этом разделительная линия получается, если формулу приравнять к единице 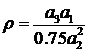 =1.
=1.
Далее запишем искомое уравнение 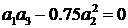 .
.
С учетом исходных данных коэффициенты, входящие в разделительное уравнение получаются следующим
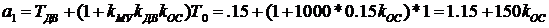 ;
;
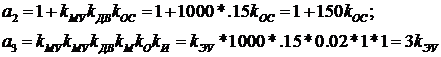
Используя выражения для коэффициентов,получим завершенный вид разделительного уравнения
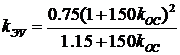 .
.
На рис.7.7. представлена разделительная линия 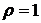 . Для определения подобласти необходимо сделать пробные вычисления параметра
. Для определения подобласти необходимо сделать пробные вычисления параметра  с обеих сторон разделительной линии. В данной задаче
с обеих сторон разделительной линии. В данной задаче 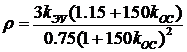 <1 в точке с координатами
<1 в точке с координатами 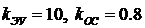 .
.
Время переходного процесса для подобласти, в которой 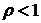 определяется по формуле
определяется по формуле 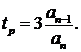 Из этой формулы получим уравнение кривой, соответствующей времени
Из этой формулы получим уравнение кривой, соответствующей времени 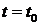 . Уравнение имеет вид
. Уравнение имеет вид 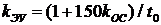 .
.
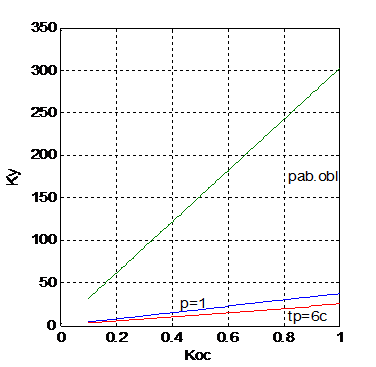
Рис. 7.7. К упражнению 34
Прежде, чем задаться временем 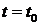 , необходимо оценить его величину в подобласти
, необходимо оценить его величину в подобласти 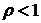 . Возьмем рабочую точку с координатами
. Возьмем рабочую точку с координатами 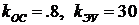 и вычислим время переходного процесса. Для этой точки
и вычислим время переходного процесса. Для этой точки 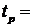 3.4с.
3.4с.
Примем 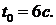 , тогда уравнение кривой на интервале
, тогда уравнение кривой на интервале 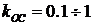 (соответствующей принятому времени) будет иметь вид
(соответствующей принятому времени) будет иметь вид 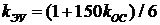 . На рис. 7.7. данная кривая соответствует нижней линии
. На рис. 7.7. данная кривая соответствует нижней линии 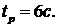
Ниже представлена программа расчета рабочей области
%3 граница, ke3, ke4-это обозначение коэффициента усиления Kэу, k1,k3,k4-это обозначение коэффициента Koc
k3=0.1:.01:1;
ke3=1.11*(1.15+150*k3).*(1+150*k3);
%4 граница
k4=0.1:.01:1;
ke4=2*(1+150*k4).*(1+150*k4)./(1.15+150*k4);
%расчет разд. линии ро=1 (к1-это Кос,Кур-это Ку)
k1=0.1:.01:1;
kyp1=.75*(1+150*k1).*(1+150*k1)./((1.15+150*k1)*3);
%Расчет линии пост. знач. времени перех.проц.
%(к5-это Кос)
t0=6
k5=0.1:.01:1;
kyt=(1+150*k5)/t0;
plot(k1,ke1,k4,ke4,k5,kyt);
%Проверка нахождения рабочей точки в рабочей области
Koc=.4
kу=250
a0=0.015;
a1=1.15+150*Koc;
a2=1+150*Koc;
a3=3*kу;
raz1=a0*a2-6*a1.^2
raz2=a0^2*a3-a1.^3
raz3=a0*a3-.5*a1*a2
raz4=a1*a3-6*a2.^2
Упражнение 35. Получить кривую переходного процесса 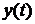 .
.
Уравнение системы автоматического регулирования имеет вид
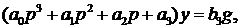 (7.6)
(7.6)
где 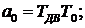
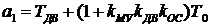 ;
; 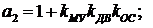
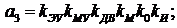
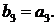
Исходные данные:
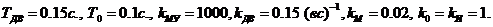
Недостающие данные для параметров 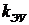 и
и 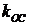 необходимо взять из рабочей области, рис.7.7. Выберем рабочую точку с координатами:
необходимо взять из рабочей области, рис.7.7. Выберем рабочую точку с координатами: 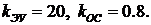 В соответствии с рис.7.7 переходный процесс должен быть апериодическим и время переходного процесса должно соответствовать примерно 6 сек.
В соответствии с рис.7.7 переходный процесс должен быть апериодическим и время переходного процесса должно соответствовать примерно 6 сек.
Решение. Уравнение (7.6) представим в виде системы уравнений состояния (2.11)
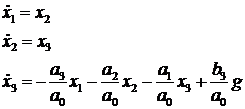 (7.7)
(7.7)
где 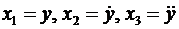 .
.
Численные значения коэффициентов уравнения с учетом исходных данных равны: 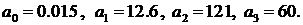
Кривая переходного процесса получается в результате численного решения (моделирования) уравнений состояния. Для решения необходимо составить файл – функцию для вычисления правых частей (7.7). С этой целью в главном меню МАТLAB выбирается команда File-New-M-file. В результате раскроется окно редактора m-файлов. В это окно необходимо ввести файл-функцию. Для рассматриваемой задачи (7.7) текст файл-функции будет таким:
Function CMO = vdp(t,х)
A0=a0; A1=a1; A2=a2; A3=a3; B3=b3; G ( t )=g;
dх1 = х(2);
dх2 = х(3);
dх3 = 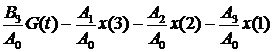 ;
;
CMO=[dх1;dх2;dх3];
Для получения решения в интервале времени [0, t0] в командном окне размещается обращение к функции ode23:
[t,х] = ode23(‘vdp’, [0, t0],[0, 0, 0]). (7.8)
.Далее на панели инструментов нажимается клавиша Enter. В этом же командном окне печатаются результаты решения. Если необходим график зависимости у(t), тогда в конце обращения к функции ode 23 ставится точка с запятой и на следующей строке формируется следующая команда plot(t, х) и опять нажимается клавиша Enter.В результате выводятся графики: 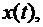
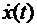 и
и 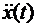 . Если необходимо вывести только одну функцию, например
. Если необходимо вывести только одну функцию, например 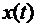 , то формируется команда plot(t, х(:, 1)).
, то формируется команда plot(t, х(:, 1)).
В обращении (7.8) в круглых скобках указываются имя функции в апострофах, в первых квадратных скобках временной интервал интегрирования, в других таких же скобках начальные значения переменных х1, х2 и х3. В данном обращении эти значения равны нулю.
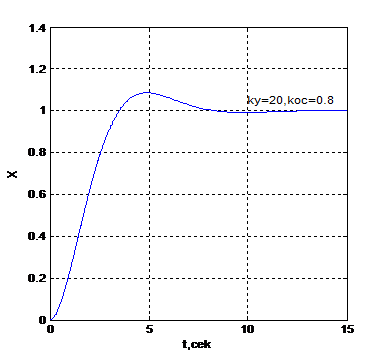
Рис. 7.8. Переходный процесс
На рис.7.8 представлена кривая переходного процесса. Видно, что время переходного процесса 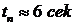 . Форма переходного процесса близка к апериодической форме. Последнее обусловлено близостью расположения рабочей точки к разделительной кривой.
. Форма переходного процесса близка к апериодической форме. Последнее обусловлено близостью расположения рабочей точки к разделительной кривой.
