Находят величину требуемой площади поперечного сечения методом

последовательных приближений, начиная со значения j =0,5 ( )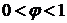

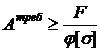. (7)

2.Определение допускаемой нагрузки. По известной площади и допускаемому

напряжению определяют величину допускаемой нагрузки

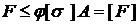. (8)

3.Проверочный расчет. По известным значениям F, A, [s] и j проверяют

выполнение условия устойчивости (6).

Величина критической силы ( 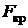) определяется по следующим формулам

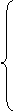
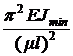, если l ³ l_пред - формула Эйлера;

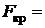
A (a - bl), если l < l_пред - формула Тетмайера – Ясинского,

где E- модуль нормальной упругости (справочная величина); J_min- минимальный

момент инерции; l- расстояние между опорами;

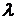- гибкость стержня; 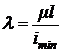; (9)

i_min-минимальный радиус инерции ;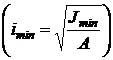

m - коэффициент приведения длины, зависящий от способа закрепления

стержня. Его значения приведены на рис.22;

l_пред - предельная гибкость стержня (l_пред =100 для стали Ст3 и l_пред =70 для дерева);

a,b- коэффициенты, используемые в формуле Тетмайера–Ясинского

(a =310 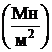, b =1,14 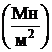– для стали Ст3).

Коэффициент запаса устойчивости

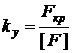. (10)

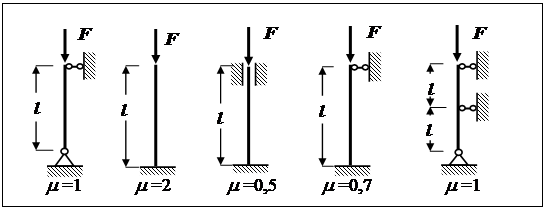
Рис.21

Определение размеров поперечного сечения (номера прокатного профиля) методом последовательных приближений

Используя формулу (7) и значения F и[s ], получаем

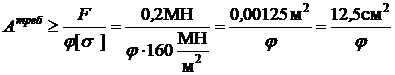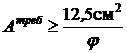, . (11)

Выразим гибкость стержня l через .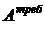

Площадь сечения 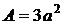, т.е. 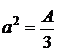или .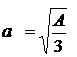

Минимальный момент инерции и минимальный радиус инерции

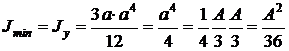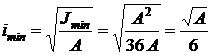; , тогда

.

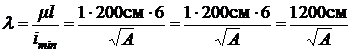Приравнивая 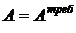, получаем 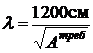. (12)

Формулы (11) и (12) используем в методе последовательных приближений.

Замечание. Для прокатных профилей (двутавр и швеллер) из справочных таблиц

по требуемой площади определяют номер профиля, минимальный

момент инерции (J_min) и минимальный радиус инерции (i_min ), а для

определения гибкости стержня используют формулу (9).

I шаг. ; ; .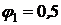

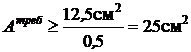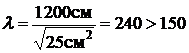В соответствии с условием задачи уменьшаем длину стержня в два раза, тогда

гибкость уменьшится тоже в два раза ( ).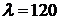

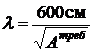Используя таблицу 6, по значению 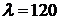находим значение 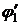=0,45.

Таблица 6

l
j	0,89	0,86	0,81	0,75	0,69	0,60	0,52	0,45	0,40	0,36	0,32

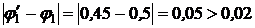; поэтому переходим к следующему шагу.

II шаг. ;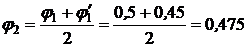

; .

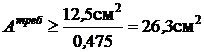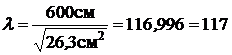Используя таблицу 6, методом линейной интерполяции определяем j¢₂:

l j

110 0,52

117 j¢₂

120 0,45

Dl₁=120-110= 10 Dj₁ = 0, 45- 0, 52= -0, 07

Dl₂=117-110= 7 Dj₂= j¢₂ - 0, 52 .

Из пропорции Dl₁ ×Dj₂ =Dl₂×Dj₁ находим

Dj₂ = 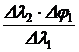; j¢₂ - 0, 52 = .

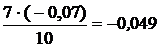Тогда j¢₂= 0, 52 - 0, 049=0, 471.

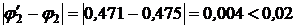. Расчет закончен. Проверяем выполнение условия устойчивости (6).

; ;

,

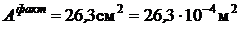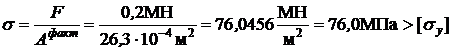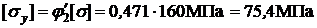где 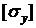-допускаемое напряжение на устойчивость.

Стержень перегружен, определяем величину перегрузки

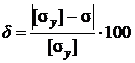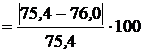% %=0,796 % <5%.

Перегрузка находится в допустимых пределах ( 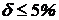), поэтому принимаем

; ;

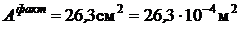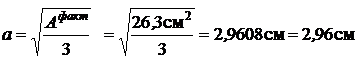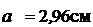; l =117; j = j¢₂ = 0, 471.

Определение величины критической силы

Так как l =117 > l_пред=100; то критическую силу определяем по формуле Эйлера

,

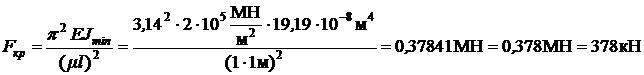где E= ; .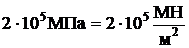

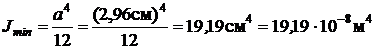Нахождение допускаемой нагрузки и коэффициента запаса устойчивости

Используя формулу (8), получаем величину допускаемой нагрузки

.

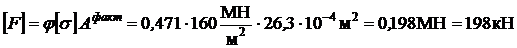Значение коэффициента запаса устойчивости вычисляем по формуле (10)

.

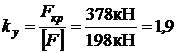Полученный коэффициент запаса устойчивости находится в требуемых для стали пределах ( 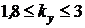).