Метод наибольшего правдоподобия

Существует два способа оценки параметров распределения: интервальный и точечный. Точечные методы указывают лишь точку, в окрестности которой находится неизвестный оцениваемый параметр. Интервальные способы дают возможность найти интервал, в котором с некоторой вероятностью (задаваемой исследователем) находится неизвестное значение параметра. Рассмотрим некоторые методы точечной оценки параметров.

Пусть имеется генеральная совокупность, Х – случайная величина, имеющая распределение р(x,Q). Если Х – дискретная, то р(x,Q) – вероятность, если Х – непрерывная, то р(x,Q) – плотность, Х₁, …, Х_n – выборка. Необходимо найти такое распределение р(x,Q), которое бы лучше всего соответствовало выборке. Соответствие выборки Х₁, …, Х_n закону распределения, содержащего параметр Q, означает, что вероятность получить тот же набор Х при другом значении параметра меньше. Приходим к следующей оптимизационной задаче – при заданных Х₁, …, Х_n определить значение параметра Θ, чтобы р(x,Q) (вероятность или плотность распределения) была наибольшей. В такой постановке х – фиксированная точка, а Θ ­– переменная. Функцию L(Θ) = р(x,Q) называют функцией правдоподобия.

Более точная математическая формулировка задачи оптимизации следующая.

Если Θ Î q – замкнутой области допустимых значений, необходимо найти такое Θ^*, чтобы

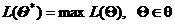. (1)

Из анализа известно, что точка максимума не изменится, если вместо L(Q) рассмотреть lnL(Q), которая называется логарифмической функцией максимального правдоподобия. Если максимум функции lnL(Q) достигается внутри допустимой области q, то в точке максимума Q^* справедливо необходимое условие экстремума

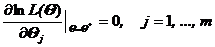(2)

Система уравнений (2) называется системой уравнений правдоподобия. Так как система (2) является лишь необходимым условие, то найденные Q^* могут быть и точками перегиба. Поэтому необходимо проверить выполнение достаточных условий экстремума (например, по знаку второй производной). Если система не имеет решений внутри области, то это означает, что решение может быть на границе области.

Так как Х – выборка и следовательно Х₁, …, Х_n – независимые, одинаково распределенные случайные величины, то

L(Q) = р(X,Θ) = р(X₁,Θ), …, р(X_n, Θ), 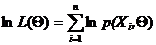. (3)

Пример 1. Пусть Х имеет нормальное распределение. Есть выборка объема n, Q₁ = a, Q₂ = s², тогда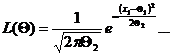

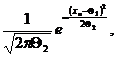
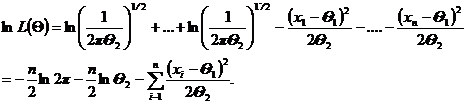
Первое уравнение системы будет иметь вид

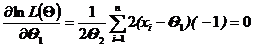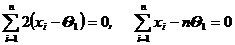, . (4)

Второе уравнение системы будет иметь вид

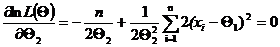или

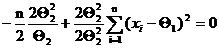
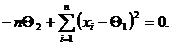(5)

Из соотношений (5), (6) составим систему (7), которая называется системой уравнений правдоподобия

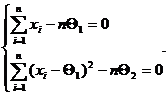(6)

Решив систему относительно неизвестных Q₁, Q₂, получим

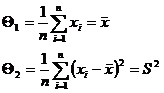
Метод моментов

Известно, что эмпирическая функция распределения (плотность) является состоятельной оценкой теоретической функции распределения (плотности), т.е. с увеличением числа наблюдений эмпирическая функция сколь угодно мало отличается от теоретической. Если теоретическая функция распределения зависит от каких-либо параметров, то для оценки этих параметров можно воспользоваться выборочными моментами. Пусть, например, плотность распределения содержит два параметра Θ₁ и Θ₂ т.е. Θ = (Θ₁, Θ₂). Первые два момента можно выразить через функцию распределения и Q следующим образом:

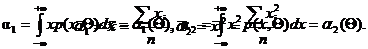Если есть выборка из генеральной совокупности, то выборочные моменты можно найти по известным формулам:

Так как выборочные моменты являются состоятельными оценками, то они с ростом n сходятся по вероятности к функциям a₁(q) и a₂(Q) в точке Θ = (Θ₁, Θ₂)

Следовательно, при больших n, a₁(Q) » 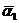, a₂(Q) » 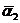. Заменяя приближенное равенство на точное, получим систему, состоящую из двух уравнений с двумя неизвестными:

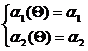, (7)

которую надо решить относительно Q₁ и Q₂.

Метод моментов содержит неоднозначность, так как можно получить систему уравнений (7), используя также и центральные моменты – 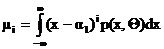, а следовательно, получим и другие значения Q₁ и Q₂.

Пример 2. Пусть имеется нормальное распределение с неизвестными параметрами:

а = Q₁, s² = Q₂.

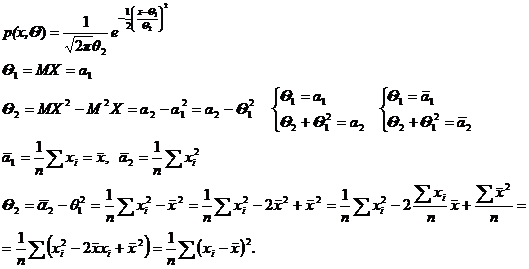Таким образом, если случайная величина имеет нормальное распределение, то оценки а и σ² вычисляются по формулам

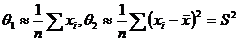
Интервальная оценка

Если получена точечная оценка неизвестного параметра по выборке, то говорить о полученной оценке как об истинном параметре довольно рискованно. В некоторых случаях, целесообразнее, получив разброс оценки параметра, говорить об интервальной оценке истинного значения параметра. В качестве иллюстрации сказанного рассмотрим построение доверительного интервала для математического ожидания нормального распределения.

Мы показали, что 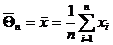– наилучшая оценка (абсолютно корректная) для математического ожидания МХ = Q, поэтому является абсолютно корректной оценкой также и для параметра a = 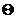нормального распределения

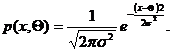
по выборке объема n. Предположим, что задана выборка Х_i, i= 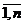. Дисперсия генеральной совокупности известна и равна s². Как далеко может находиться случайная величина от неизвестного математического ожидания Q, оценкой которого она является? Чтобы ответить на этот вопрос, рассмотрим случайную величину 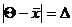, представляющую отклонение от Q. Отклонение D может изменяться от 0 до +¥, но нас интересует, прежде всего, вероятность того, что отклонение D не превысит предельной ошибки e допустимого уровня

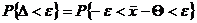. (8)

В формуле (8) только величина является случайной, поэтому вероятность Р зависит только от распределения .

Очевидно, что события A = {–e<Q– <e} и B = {–e+ <Q<e+ } эквивалентны, так как если произойдет событие А, то произойдет и событие В и наоборот. Поэтому

Р{–e+Q< <e+Q} = Р{–e+ <Q<e+ }. (9)

Таким образом, если 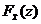– функция распределения непрерывной, случайной величины , то

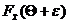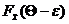Р{–e+Q< <e+Q}= – (10)

Определим функцию распределения 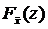случайной величины , где х_i Î N(q,s²). Известно, что линейная функция от нормальных случайных величин является нормальной. Поэтому – нормальная, а нормальная случайная величина задается двумя параметрами – математическим ожиданием и дисперсией, но

.

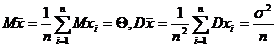Таким образом, плотность распределения имеет вид

.

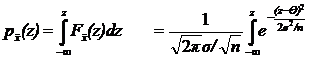Поэтому Р{-e+Q< <e+Q}= .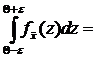

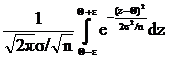В полученном интеграле произведем замену переменных u= 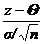, получим

Р{-e+Q< <e+Q}=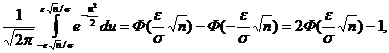

где Ф(z) – функция распределения нормированной нормальной случайной величины.

Таким образом,

Р{-e+ <Q<e+ }= 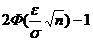. (11)

Если обозначить -e+ = Q₁, e+ = Q₂, то получим интервал (Q_1, Q₂), который накрывает с вероятностью, равной 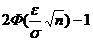, неизвестную величину Q и эта вероятность не зависит от Q, т.е., она одна и та же для любых значений Q. Чтобы найти сам интервал, надо по выборке вычислить и задать e.

Можно по заданной вероятности Р найти концы интервала. Для этого надо воспользоваться формулой 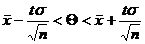, где t – значение аргумента функции Лапласа, при котором Ф(t ) = 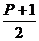, e = 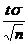.