Лекция 8. понятие многомерной случайной величины

Очень часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин , , …, которую называют также многомерной (п-мерной) слу­чайной величиной, или случайным векторомX = ( , , …, ).

Приведем примеры многомерных случайных величин.

Пример 1. Успеваемость выпускника вуза характеризуется системой п случайных величин , , …, –оценками по различным дисциплинам, проставленными в приложении к диплому.

Пример 2. Погода в данном месте в определенное время суток может быть охарактеризована системой случайных величин: – температура; – влажность; 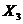– давление; 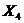– скорость ветра и т.п.

Пример 3. Состояние здоровья человека (температура тела, давление, параметры крови и т.д.).

В теоретико-множественной трактовке любая случайная ве­личина 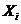(i = 1, 2, …,n )есть функция элементарных событий w, входящих в пространство элементарных событий W (wÎW). Поэтому и многомерная случайная величина есть функция элементарных событий w:( , , …, )= f(w),т.е. каждому элементарному событию w ставится в соответствие несколько действительных чисел 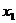, , 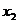…, 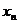которые приняли случайные величины , ,…, в результате испытания. В этом случае вектор x = ( 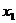, , 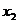…, 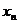) называется реализацией случайного вектора X = ( , , …, ).

Случайные величины , , …, могут быть как дискретными (см. пример 1), так и непрерывными (см. пример 2,3).

Задача 1.Подбрасывают одновременно две игральные кости; случайная величина X – сумма очков, полученных в результате испытания; случайная величина Y – их произведение. Показать, что двумерная случайная величина (X, Y)есть функция элементарных исходов (событий) w.

Решение. Множество элементарных исходов (пространство элементарных событий) состоит из 36 элементарных исходов, т.е.

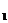W = {w , w , …, w 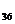} = {1/1, 1/2, ...,1/6, 2/1, 2/2, ...,2/6, ...,6/1, 6/2, ...,6/6},

где элементарный исход, например, w 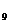= 2/3 означает выпадение при подбрасывании первой игральной кости 2 очков и второй кости – 3 очков. Если результатом испытания является какой-нибудь элементарный исход (событие) w 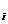, то случайные величи­ны Х и Y получат определенные значения; например, при w 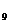= 2/3 Х = 5, Y = 6.Совокупность этих значений (X, Y)представляет, таким образом, функцию элементарных исходов (событий) w, т.е.,

w 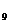= 2/3 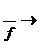(5, 6).

Геометрически двумерную (X, Y)и трехмерную (X, Y, Z)слу­чайные величины можно изобразить случайной точкой или слу­чайным вектором плоскости Оху или трехмерного пространства Oxyz; при этом случайные величины X, Y или X, Y, Z являются составляющими этих векторов. В случае n-мерного пространства (п > 3) также говорят о случайной точке или случайном векторе этого пространства, хотя геометрическая интерпретация в этом случае теряет свою наглядность.

Наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном или счетном множестве возможных значений многомерной случайной величины такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X, Y),то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения, в каждой клетке (i,j)которой располагаются вероятности произведения событий p = P[X = x 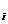,Y = y ].

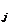Так как события [X = x 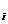, Y = y_j] (i = 1, 2, …, n; j = 1, 2, …, m), состоящие в том, что случайная величина X примет значение x_i, а случайная величина Y – значение y_j, несовместны и единст­венно возможны, т.е. образуют полную группу, то сумма их ве­роятностей равна единице, т.е.

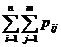= 1.

Итоговые столбец или строка таблицы распределения (X, Y) в совокупности со значениями X, Y представляют соответственно распределения одномерных составляющих (x_i, p_i) или (y_j, p_j).

	y	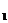…	yj	…	Y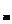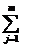
x	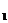p	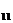…	p1j	…	p1m	p1·
…	…	…	…	…	…	…
x	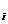p	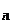…	pij	…	pim	pi·
…	…	…	…	…	…	…
x	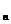p	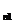…	pnj	…	pnm	pn·
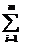	p·	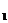…	P ·j	…	P·m

Действительно, распределение одномерной случайной величины Xможно получить, вычислив вероятность события X = х_i, (i = 1, 2, …, n) как сумму вероятностей несовместных событий

P(X = x_i) = p_i× = P[(X = x_i)(Y = y₁)+…+(X = x_i)(Y = y_j)+…+(X = x_i)(Y = y_m)] =

p_i1+…+p_ij+…+p_im = .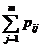

Аналогично Р(Y = y_j) = p× _j = .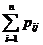

Таким образом, чтобы по таблице распределения найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности p_ij из соответствующей этому значению строки (столбца) данной таблицы.

Если зафиксировать значение одного из аргументов, например, положить Y = y_j, то полученное распределение случайной величины X называется условным распределением X при условииY = y_j. Вероятности P(x_i/y_j) = p_j(x_i) этого распределения будут условными вероятностями события X = x_i, найденными в предположении, что событие Y = y_j произошло. Из определения условной вероятности P(X/Y) = P_y X = P(XÇY)/P(Y) имеем

Р(_Xi /_Yj ) = p_j(x_i) = 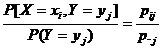. (1)

Аналогично условное распределение случайной величины Y при условии X = x_i задается с помощью условных вероятностей

Р(y_j /x_i ) p_i(y_j) = 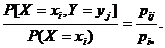(2)

Задача 2.Закон распределения дискретной двумерной случайной величины (X,Y) представлен в таблице

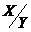	-1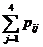
	0,10	0,25	0,30	0,15	0,8
	0,10	0,05	0,00	0,05	0,2
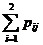	0,2	0,3	0,3	0,2

Найти:

а) законы распределения одномерных случайных ве­личин X и Y;

б) условные законы распределения случайной величины X при условии Y = 2 и случайной величины Y при условии X = 1;

в) вычислить P{Y< X).

Решение.

а) случайная величина X может принимать значения:

Х = 1 с вероятностью p₁ = 0,10 + 0,25 + 0,30 + 0,15 = 0,8;

X = 2 с вероятностью p₂ = 0,10 + 0,05 + 0,00 + 0,05 = 0,2,

т.е. ее закон распределения X имеет вид

xi
pi	0,8	0,2

Аналогично закон распределения Y имеет вид

yj	-1
pj	0,2	0,3	0,3	0,2

б) условный закон распределения X при условии, что Y = 2, получим, если вероятности p_ij, стоящие в последнем столбце исходной таблицы, разделим на их сумму, т.е. на P(Y = 2) = 0, 2 (например, 0,75 = 0,15/0,2). Получим таблицу распределения P ( )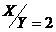

xi
pj(xi)	0,75	0,25

Аналогично для получения условного закона распределения Y при условии X = 1, вероятности p_ij, стоящие в первой строке исходной таблицы, делим на их сумму, т.е. на P(X = 1) = 0, 8 (например, 0,125 = 0,1/0,8). Получим таблицу распределения P( )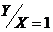

yj	-1
pi(yj)	0,125	0,3125	0,375	0,1875

в) для нахождения вероятностей P(Y < X) складываем вероятности событий p_ij из исходной таблицы, для которых y_j < x_i. Получим

P(Y < X) = 0,10 + 0,25 + 0,10 + 0,05 + 0,00 = 0,5.