Теорема о связи бесконечно малой функции, имеющей предел.

Если функция ƒ(х) имеем предел, равный b, то ее можно представить как сумму числа b и бесконечно малой функции α(х), т.е. 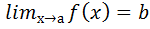, то ƒ(х)=b+α(х), где α(х)- бесконечно малая величина.

Арифметические свойства пределов функции:

1)

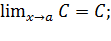
2) ;

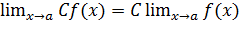3) ;

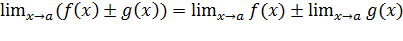4) ;

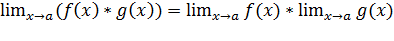5)

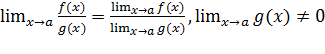
Доказательства арифметических свойств пределов:

Теорема 1. Сумма сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов исходных последовательностей.

Доказательство: Пусть x_n→a , y_n→b, x_n→a+a_n

a_n- бесконечно малая последовательность, y_n=b+β_n , β_n-беск. малая последов.

x_n+y_n=(a+b)+(a_n+β_n) x_n+y_n→a+b

Теорема 2.Еслиx_n→a, y_n→b, тоx_n-y_n → a-b

Теорема 3. Еслиx_n→a, y_n→b, тоx_n*y_n → a*b

Доказательство: x_n=a+a_n, a_n– бесконечно малая последовательность, y_n=b+β_n , β_n-беск. малая последов.

x_n*y_n=(a+a_n)*(b+β_n)=a*b+a*β_n+b*a_n+a_n*β_n=a*b+γ_n,гдеγ_n=a*β_n+b*a_n+a_n*β_n

x_n*y_n→a*b

Теорема 4.Еслиx_n→a, y_n→b≠0, тоx_n/y_n=a / b

******************************

Теорема о двух милиционерах — теорема в математическом анализе о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом

Теорема. Если функция y=f(x) такая, что ф(x)≤f(x)≤ψ(x) для всех x {\displaystyle x} в некоторой окрестности точки a {\displaystyle a}, причём функции ф(x) и ψ(x)имеют одинаковый предел приx→a, то существует предел функции y=f(x) при x→a, равный этому же значению, то есть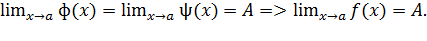

Доказательство леммы о двух милиционерах:

Из неравенства ф(x)≤f(x)≤ ψ(x) получаем неравенство ф(x)-A≤f(x)-A≤ ψ(x)-A.

Тогда верно неравенство 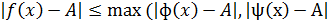). Условие 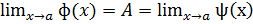позволяет предположить, что для любого ɛ>0 существует окрестность U_а, в которой верны неравенства 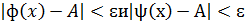. Из изложенной выше оценки максимумом следует, что 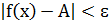при xϵU_a, что удовлетворяет определению предела, т.е. .

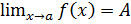Первый замечательный предел

Используется для раскрытия неопределённости .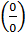

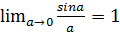–первый замечательный предел.

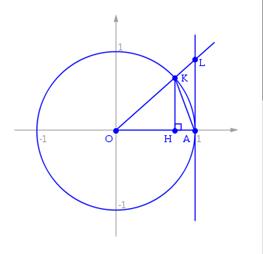- Чертёж для док-ва

Доказательство первого замечательного предела:

Виды неопределённостей: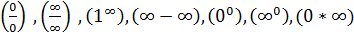

Где 0 – бесконечно малая величина, а ∞ - бесконечно большая величина, по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Для раскрытия неопределённостей используются различные методы преобразований, замечательные пределы(первый и второй).

Предел сложной функции.

Теорема 1. Если функцияy=f(x) имеет в точке aконечный пределb и не принимает значения b в некоторой проколотой окрестности U∘(a) этой точки, а функция g(y) имеет в точке b конечный предел c, то сложная функция g(f(x)) имеет предел в точке a, равный c.

Эту теорему нетрудно распространить на суперпозицию более двух функций. Она позволяет использовать замену переменных при вычислении пределов сложных функций по формуле:

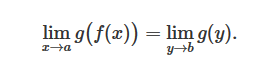
При этом говорят, что под знаком предела в левой части сделана замена f(x)=y. Данная теорема и возможность замены переменных остаются в силе, если хотя бы одна из точек a,b,c будет соответствовать одной из бесконечных точек +∞ или −∞ (или их объединению ∞) на расширенной числовой прямой.