Понятие размещения. Число размещений с повторениями и без повторений
В комбинаторике размещением из n по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества. Или иначе, размещение из n по k – это k-элементное подмножество n-элементного множества.
Число размещений из n по k без повторений
Пусть у нас есть множество X, состоящее из n элементов:
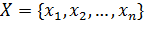
и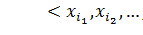 
– некоторое размещение элементов этого множества.
1-й элемент этого множества мы можем выбрать n способами;
2-й элемент – n-1 способами;
3-й элемент – n-2 способами.
Размещая таким образом элементы множества X до k-го, мы получим, что k-й элемент мы можем выбрать n-(k-1) способами.
Тогда мы получаем, что по правилу произведения количество этих k-элементных упорядоченных подмножеств множества Х будет равно
.
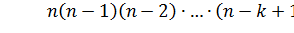То есть получаем, что число размещений из n элементов по k без повторений равно:
.
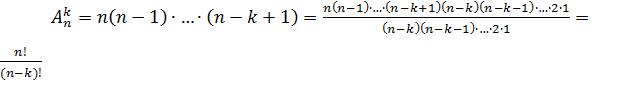То есть получаем формулу для вычисления числа размещений без повторений из n элементов по k:
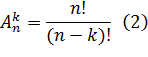
Замечание!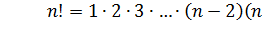 
(читается «n факториал»).
Число размещений из n по k с повторениями
Пусть у нас есть множество X, состоящее из n элементов:
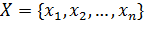
и 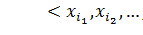– некоторое размещение элементов этого множества, однако на этот раз элементы в данном размещении могут повторяться. Обозначим 
(или 
) число размещений с повторениями.
Тогда 1-й элемент мы можем выбрать n способами; 2-й элемент – n способами; 3-й элемент – n способами, и т.д., и k-й элемент мы можем выбрать тоже n способами.
Таким образом, мы получаем, что число размещений с повторениями можно вычислить следующим образом:
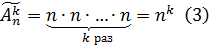
То есть получаем формулу: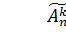 
.
Число подмножеств конечного множества
Рассмотрим его на примере данного множества A, состоящего из трех элементов: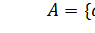 
. Перечислим все подмножества множества А:
;
;
;
;
;
;
;
.
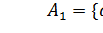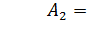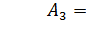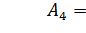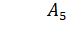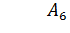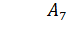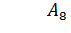Обозначим 
множество всех подмножеств множества А. Тогда получаем,что число элементов множества равно 8, при условии, что число элементов множества А равно 3.
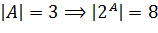
Пусть множество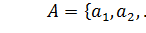 
.
Каждому подмножеству 
множества А поставим в соответствие n-элементный набор, состоящий из 0 и 1:
;
;
;
;
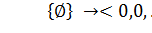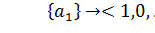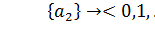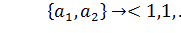И т.д.
.
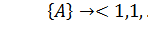Тогда число всех подмножеств равно числу всех таких наборов, а оно, в свою очередь, вычисляется по формуле:
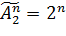
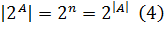
Выводы к главе 1
Комбинаторика формировалась как наука в течение довольно долгого периода, и она все еще развивается. Она широко используется как в обиходе (например, в играх), так и в других науках, и тесно связана с различными областями математики (алгеброй, геометрией, теорией вероятностей и др.). Иногда в широком понимании под комбинаторикой подразумевают более обширную область дискретной математики, включающую, в том числе, и теорию графов. Однако наиболее знакомой для нас является вероятностная и перечислительная комбинаторика. Первая изучает вопрос вероятности обладания некоторого множества конкретным свойством, вторая же рассматривает задачи о перечислении или исчислении количества различных конфигураций (перестановок, размещений, сочетаний). Данная работа сфокусирована на размещениях и исследовании их теоретических и практических особенностей.
По окончанию первой главы мы можем заключить, что комбинаторика имеет интересную историю собственного становления как науки. А ее различные разделы имеют широкий спектр применения в различных сферах знаний.
Глава 2. Примеры решения задач по комбинаторике