Разложение в ряд Фурье функции продолженной произвольным способом

Достроим функцию на участке [-π;0).

Тогда получим

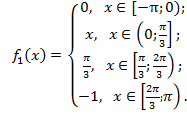
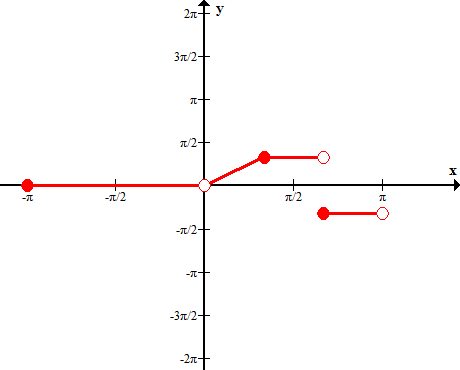
Функция непериодическая, кусочно-гладкая, задана на интервале [-π;π]. Функция имеет на промежутке [-π;π] конечное число точек разрыва первого рода.

Сумма ряда в точках разрыва функции сходится к значению самой функции, а в точках разрыва к величине f(x₀), где x₀ – точка разрыва.

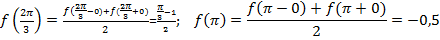
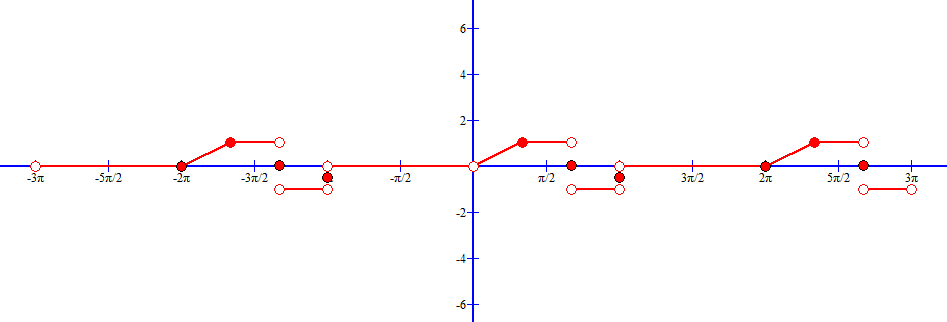
Производная так же непрерывна везде, кроме конечного числа точек разрыва первого рода.

Вывод: функция удовлетворяет условиям Дирихле.

Так как отсутствует симметрия относительно оси OY, а также центральная симметрия, то рассматриваемая функция произвольна.

Представление функции рядом Фурье:

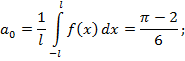
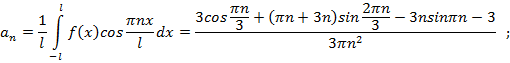
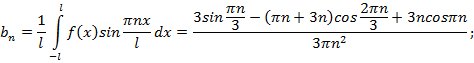
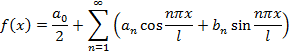
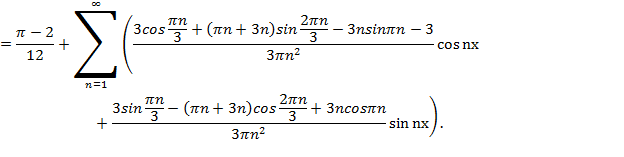
Построим первые три гармоники и одну бесконечно большую гармонику для найденного ряда.

1-ая гармоника

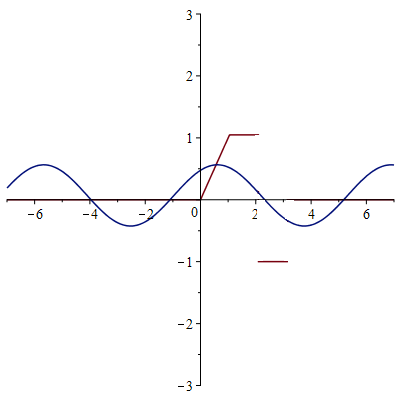
2-ая гармоника

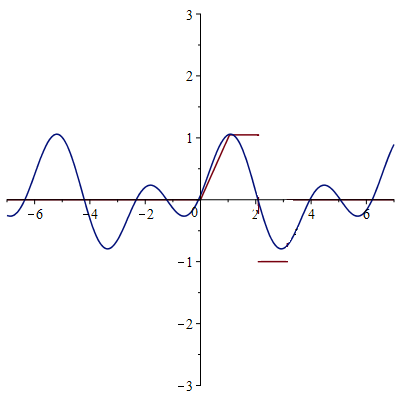
3-я гармоника

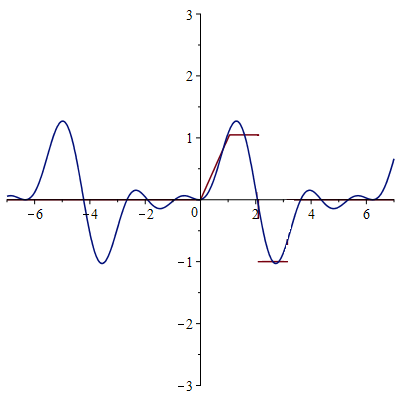
Сумма 100 гармоник

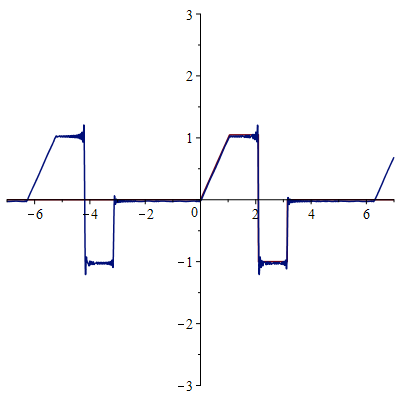
Построим амплитудный и фазовый спектры функции по формулам:

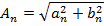
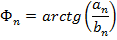
Амплитудный спектр для данной функции:

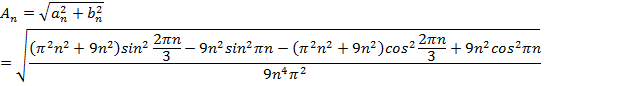
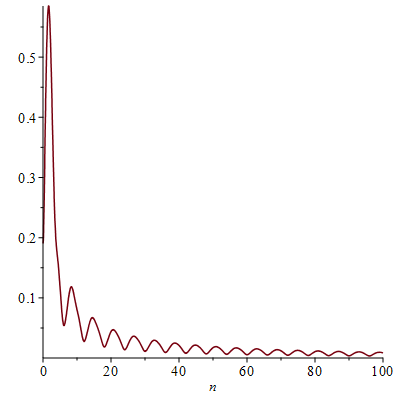
Рассчитаем фазовый спектр для данной функции:

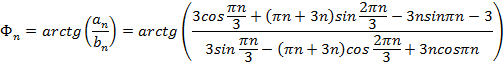
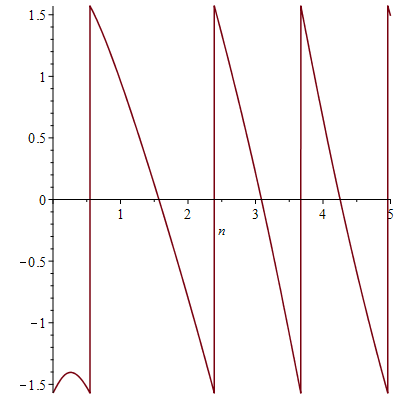
Вычислим среднеквадратическую ошибку между исходной функцией f(t) и частичной суммой Фурье для t, принадлежащих промежутку задания f(t).

Среднеквадратическую ошибку вычисляем по формуле:

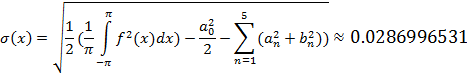
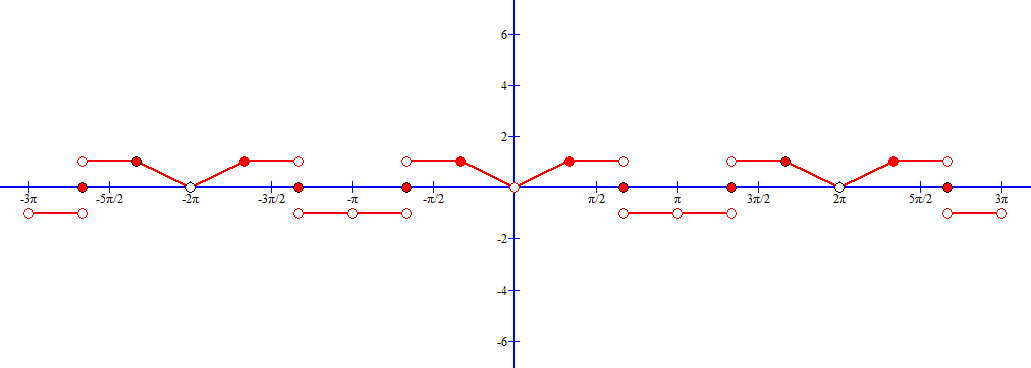
Разложение в ряд Фурье функции продолженной четным способом

Достроим функцию на участке (-π;0):

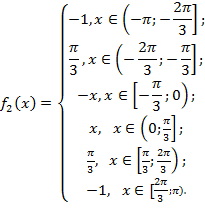
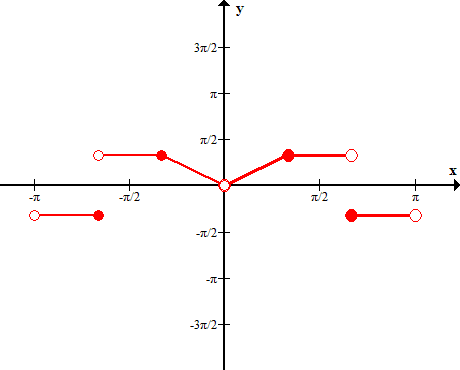
Функция непериодическая, задана на интервале (- 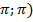, имеет конечное число точек разрыва первого рода. Производная непрерывна везде, кроме конечного числа точек разрыва первого рода.

Вывод: функция удовлетворяет условию разложения в ряд Фурье.

Так как функция симметрична относительно оси ОУ, четная, то:

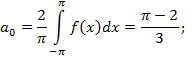
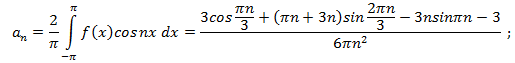
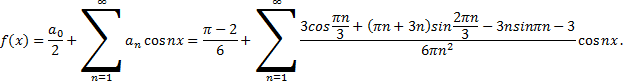
1-ая гармоника

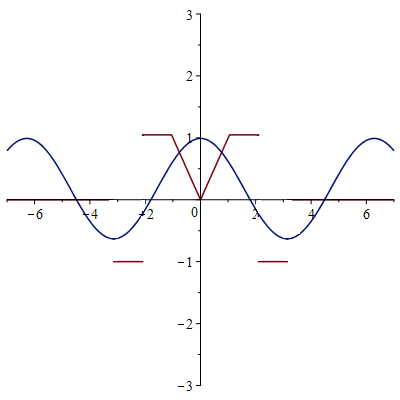
2-ая гармоника

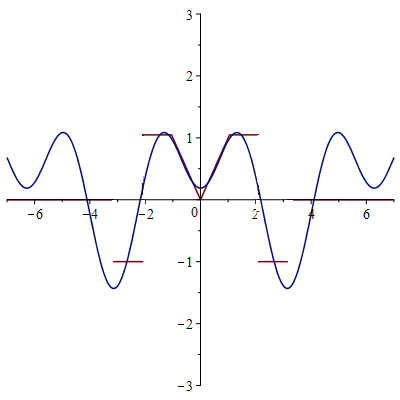
3-я гармоника

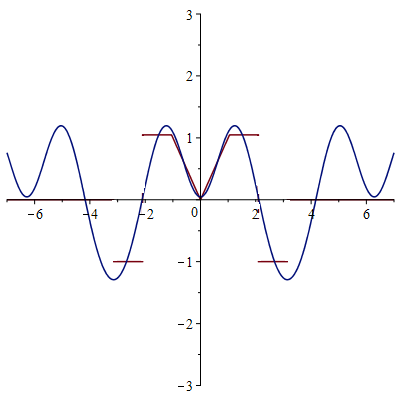
Сумма 100 гармоник

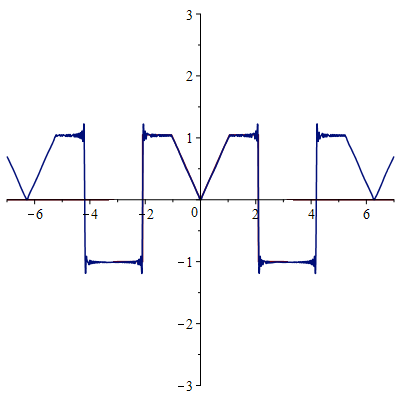
Сумма ряда в точках функции сходится к значению самой функции, в точках разрыва к величине 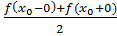, где х₀-точка разрыва.

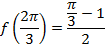
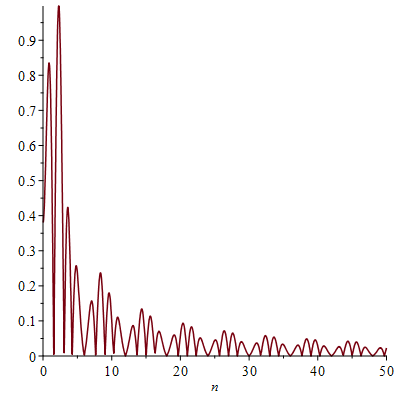
Построим амплитудный спектр:

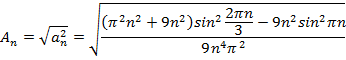
Вычислим среднеквадратическую ошибку:

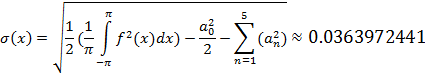
Разложение в ряд Фурье функции продолженной нечетным способом

Достроим функцию на участке (-π;0):

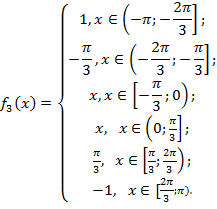
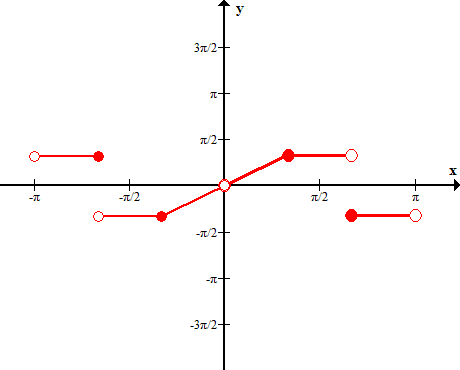
Функция непериодическая, задана на интервале (- 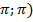, имеет конечное число точек разрыва первого рода. Производная непрерывна везде, кроме конечного числа точек разрыва первого рода.

Вывод: функция удовлетворяет условию разложения в ряд Фурье.

Сумма ряда в точках разрыва функции сходится к значению самой функции, а в точках разрыва к величине 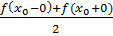, где x₀ – точка разрыва.

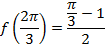
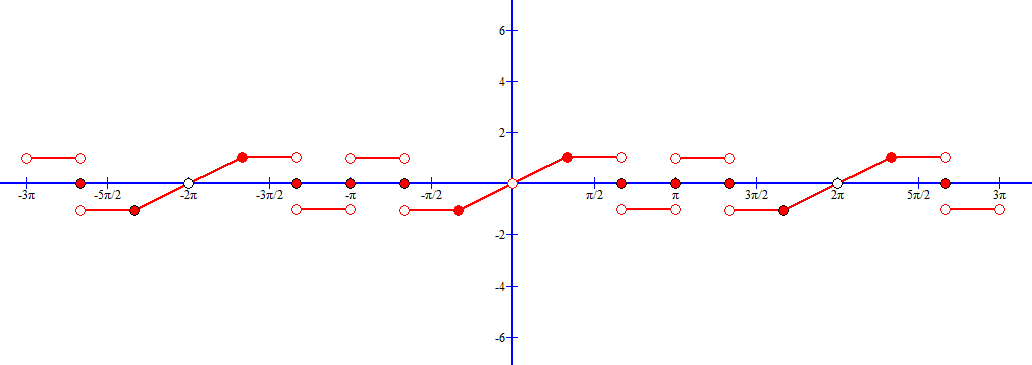
Так как присутствует симметрия относительно начала координат, то рассматриваемая функция нечетная.

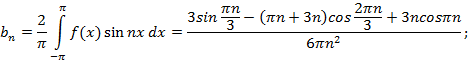
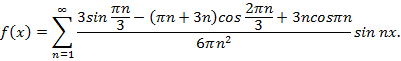
1-ая гармоника

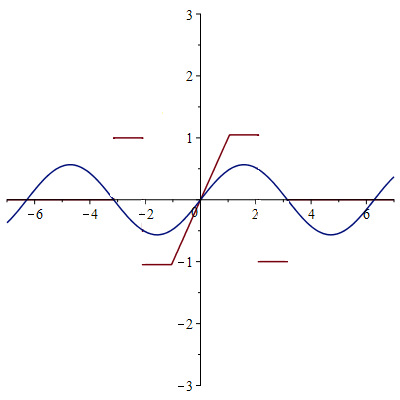
2-ая гармоника

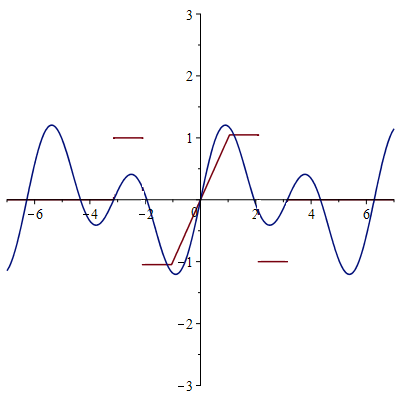
3-я гармоника

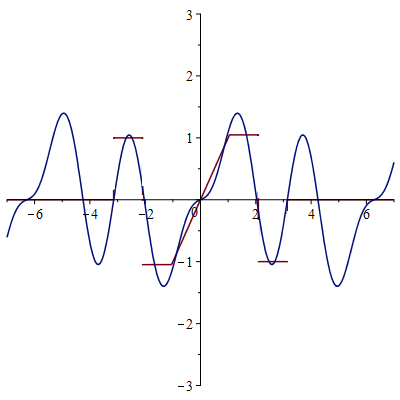
Сумма 100 гармоник

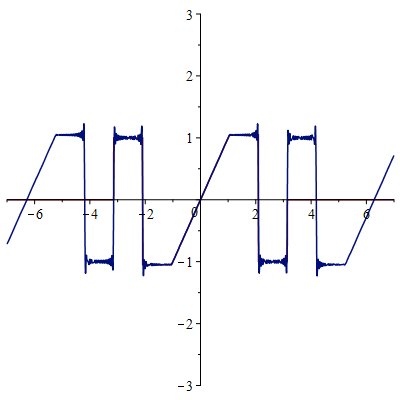
Амплитудный спектр:

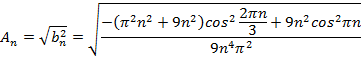
Вычислим среднеквадратическую ошибку:

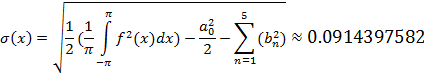
Вывод

Таким образом, разложение в ряд Фурье упрощает вычисление значения функции, а в некоторых случаях, это единственный способ решения.

Исходя из выполненной нами курсовой работы, видно, что при увеличении количества сумм гармоник, ряд Фурье все больше, и больше приближается к исходной функции, а в точках разрыва первого рода значение функции численно равно среднему арифметическому между левым и правым пределом.

Погрешности вычислений в каждом из способов разложения функции в ряд Фурье указывают на то, что наиболее точный график получается при разложении по косинусам, так как 0.0363972441, 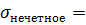0.0914397582, 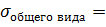0.0286996531.

Список литературы

1. Власова Е.А. Ряды. М. : МГТУ им. Н. Э. Баумана, 2000. – 612 с.

2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. М.:АСТ: Астрель, 2005. – 654 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 2. М.: Наука, 1985. – 560 с.

4. Письменный Д.Т. Конспект лекций по высшей математике. Полный курс. М.: Айрис-пресс, 2011. – 608 с.

5. http://www.mathprofi.ru/

6. http://ru.wikipedia.org

7. http://www.math24.ru/definition-of-fourier-series.html