Устойчивость плоской формы изгиба тонких балок
Пусть на торцы балки действуют моменты m (см.рис.16.1). Верхние волокна при этом сжимаются
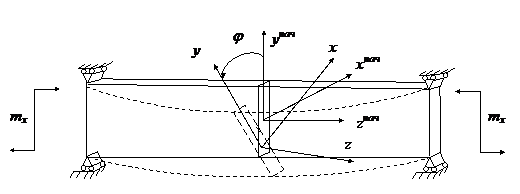
Рис.16.1
При больших напряжениях верхняя часть балки может потерять устойчивость и изогнуться из плоскости, как показано на рис.16.16.
Обозначим через j угол отклонения сечения от вертикальной оси 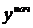 , прогиб (т.е. перемещение центра тяжести сечения вдоль оси
, прогиб (т.е. перемещение центра тяжести сечения вдоль оси 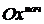 ) через u. Если посмотреть на сечение с конца оси z и изобразить момент m в виде вектора, то получим картину, приведенную на рис.16.2. Тогда получим, что согласно определению изгибающий момент относительно оси у будет:
) через u. Если посмотреть на сечение с конца оси z и изобразить момент m в виде вектора, то получим картину, приведенную на рис.16.2. Тогда получим, что согласно определению изгибающий момент относительно оси у будет:
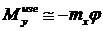 (16.1)
(16.1)
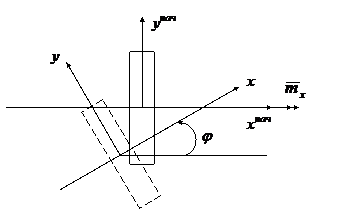
Рис.16.2
Поскольку кривизна оси балки пропорциональна 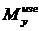 , то получим
, то получим
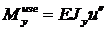 (16.2)
(16.2)
Подставив сюда (16.1) получим уравнение
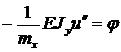 (16.3)
(16.3)
Далее рассмотрим связь крутящего момента с моментом m. Для этого необходимо посмотреть на балку с конца оси у (см.рис.16.3).
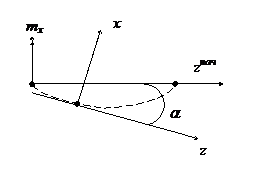
Рис.16.3
Согласно определению крутящий момент – это момент относительно оси z. Тогда, как видно из рис.16.3:
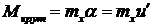 (16.4)
(16.4)
Здесь учтено, что на рисунке 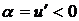 .
.
Крутящий момент 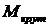 связан с j соотношением
связан с j соотношением
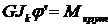 . (16.5)
. (16.5)
Тогда из (16.4) и (16.5) вытекает связь
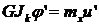 (16.6)
(16.6)
Подставляя сюда j из (16.3) получим уравнение относительно u:
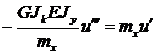 (16.7)
(16.7)
Обозначим
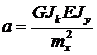 (16.8)
(16.8)
Тогда получим
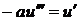 (16.9)
(16.9)
Условиям закрепления удовлетворяет функция
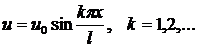 (16.10)
(16.10)
Здесь 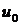 - некоторая константа.
- некоторая константа.
Подставив u в (16.9) получим:
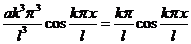 . (16.11)
. (16.11)
Подстановка сюда 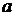 по формуле (16.8) дает:
по формуле (16.8) дает:
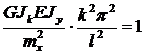 .
.
Отсюда:
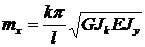 (16.12)
(16.12)
Минимального значения момент 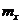 при потере устойчивости достигает тогда, когда k = 16.
при потере устойчивости достигает тогда, когда k = 16.
Если концы защемлены, то вместо (16.10) надо брать функцию
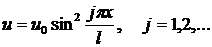 (16.13)
(16.13)
Тогда граничные условия будут также выполняться. Подстановка (16.13) в (16.9) дает выражение вида
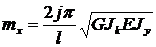 . (16.14)
. (16.14)
Снова минимального значения момент 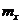 достигает при j = 16.
достигает при j = 16.
Таким образом, в обоих случаях получаем формулу вида
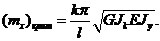 (16.15)
(16.15)
При шарнирном закреплении k = 1, при защемлении k = 2. Аналогично можно получить, что при других видах закрепления 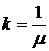 , где m - коэффициент приведенной длины, введенный для обычных задач о потере устойчивости сжатых стержней.
, где m - коэффициент приведенной длины, введенный для обычных задач о потере устойчивости сжатых стержней.
Устойчивость пластин
Рассмотрим сжатие пластины a×b×h давлениями рх , рy , рхy , (см.рис.17.1).
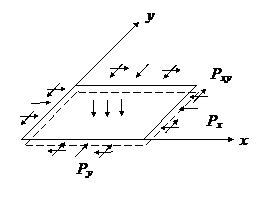
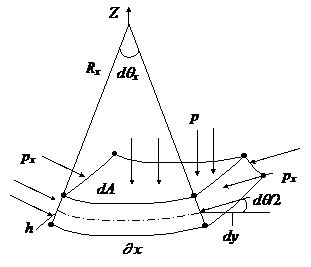
Рис.17.1 Рис.17.2
Из рисунка 17.2 видно, что на ось Z проецируется не только сила
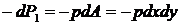 , (17.1)
, (17.1)
но и сила, вызванная давлением рх:
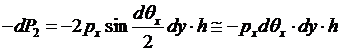 . (17.2)
. (17.2)
Суммарно получаем
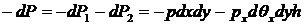 . (17.3)
. (17.3)
Деля на площадь 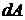 получим суммарное (приведенное) давление рприв.:
получим суммарное (приведенное) давление рприв.:
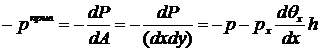 . (17.4)
. (17.4)
Согласно определению изменение угла наклона 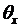 на единицу длины есть кривизна линии, т.е.
на единицу длины есть кривизна линии, т.е.
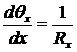 . (17.5)
. (17.5)
Таким образом, получим, что
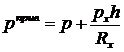 . (17.6)
. (17.6)
При малых углах 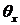 имеет место связь:
имеет место связь:
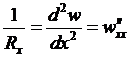 . (17.7)
. (17.7)
Окончательно находим, что
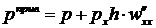 . (17.8)
. (17.8)
В случае дополнительного воздействия (кроме 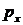 ) давлений
) давлений  и
и 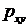 получим
получим
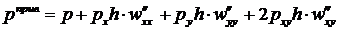 . (17.9)
. (17.9)
Подставляя в уравнение Софи-Жермен получим
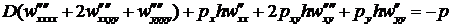 . (17.10)
. (17.10)
Это уравнение равновесия элемента пластины при продольно поперечном изгибе.
Если нет поперечных воздействий, т.е. 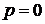 , то (17.10) называется уравнением устойчивости элементов пластины. Оно примет вид:
, то (17.10) называется уравнением устойчивости элементов пластины. Оно примет вид:
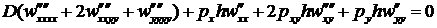 . (17.11)
. (17.11)
Рассмотрим простой случай, когда имеется лишь 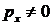 , а пластина шарнирно опёрта. Тогда на краях должны выполняться условия:
, а пластина шарнирно опёрта. Тогда на краях должны выполняться условия:
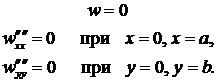 (17.12)
(17.12)
Этим условиям удовлетворяет функция:
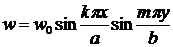 , (17.13)
, (17.13)
где 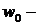 некоторая константа (максимальный прогиб),
некоторая константа (максимальный прогиб), 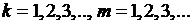
Подстановка (17.13) в (17.11) после сокращения на 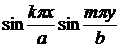 дает:
дает:
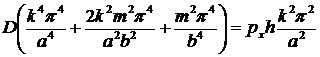 . (17.14)
. (17.14)
Отсюда находим
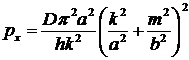 . (17.15)
. (17.15)
Для отыскания 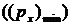 , которое приводит к изгибу пластины от сжимающего давления
, которое приводит к изгибу пластины от сжимающего давления 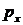 , необходимо перебрать значения
, необходимо перебрать значения 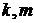 . Это даст критическое давление
. Это даст критическое давление 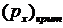 . Например, для
. Например, для 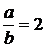 получим:
получим:
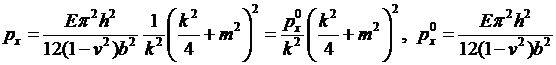 (17.16)
(17.16)
Составим таблицу значений 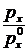 :
:
 m k m k | |||
| 1,56 | 18,06 | 85,6 | |
| 6,25 | |||
| 2,64 | 4,34 | 14,06 |
Значит, пластина потеряет устойчивость при
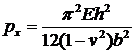 (17.17)
(17.17)
Сравним с 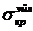 при
при 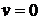 . Тогда из (17.17) при
. Тогда из (17.17) при 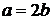 получим:
получим:
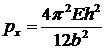 . (17.18)
. (17.18)
По Эйлеру
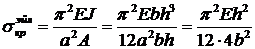 . (17.19)
. (17.19)
Таким образом, пластина выдержит в 16 раз больше.
Рассмотрим теперь квадратную пластину. Тогда 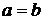 , а минимизация (17.15) дает
, а минимизация (17.15) дает 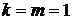 . Тогда:
. Тогда:
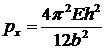 (17.20)
(17.20)
Таким образом, квадратная пластина выдержит столько же, сколько пластина двойной длины.
РасчЕт тонких оболочек
Особенности работы оболочек заключаются в следующем.
1. Они обладают прочностью и жесткостью, которые превышают в десятки и сотни раз, соответственно, прочность и жесткость пластин и балок.
2. Большая часть оболочки при плавных нагрузках работает только на растяжение или сжатие, на изгиб работает узкая полоса по ширине в несколько толщин, вблизи закреплений, т.е., в отличие от пластин и балок, усиливать оболочку приходится только вблизи закреплений.
