Точные решения задачи об изгибе жестких пластин

Решение задачи об изгибе защемленной эллиптической пластины

Рассмотрим эллиптическую пластину, жестко заделанную по краям.

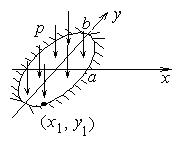
Рис.14.14

Рассмотрим случай p(x,y) = const (точное решение можно найти только для этого случая). Решение ищем в виде:

.

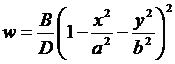где a, b - полуоси эллипса, D – цилиндрическая жесткость пластины, B – константа, которая определяется из уравнения Софи-Жермен:

.

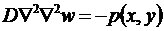Подставляя w, получим:

.

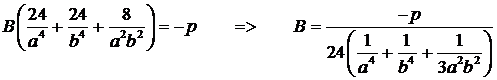Проверим выполнение условий закреплений.

Если взять точку (х₁, у₁) на границе, то для нее выполняется уравнение эллипса 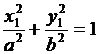. Подставляя это в уравнение для w, видим, что w=0 в точке (х₁, у₁).

Проверим выполнение условия w¢_x=0.

.

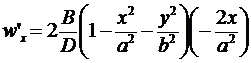С учетом уравнения эллипса для точки х₁, у₁, получим w’_x=0.Аналогично получим, что w’_у=0 в точке (х₁, у₁).

Итак, во всех точках контура w’_x=0, w’_у=0. Следовательно, в любом направлении, в том числе и по нормали к контуру, угол наклона пластины будет равен нулю.

Задача о свободно опертой прямоугольной пластине под синусоидальной нагрузкой

Свободное опирание часто изображают штриховой линией, как это показано на рис. 14.15. Используем для аппроксимации нагрузки (например, от сыпучего материала) следующую функцию (рис 14.16):

.

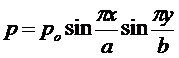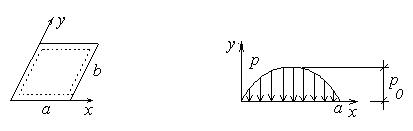
Рис.14.15 Рис.14.16

Запишем уравнение Софи-Жермен:

.

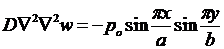Очевидно, что w надо искать в виде:

.

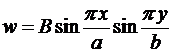Тогда:

.

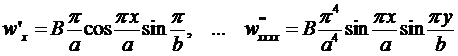В результате подстановки в уравнение Софи-Жермен получим:

.

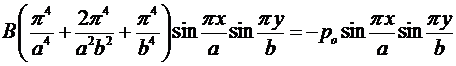Отсюда:

.

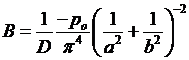Проверим, выполняются ли условия закрепления. На границах либо х = 0, либо у = 0, либо х = а, либо у = b. Тогда во всех случаях

.

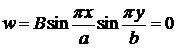Таким образом, условия закрепления выполняются.

Проверяем, выполняются ли уравнения равновесия граничных элементов.. Должно быть 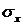=0 для любого у при х = 0 и при х = а. Имеем:

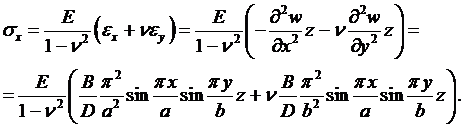
При х=а имеем:

.

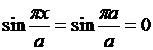Отсюда σ_х º 0.

Аналогично на других границах. Таким образом, уравнения равновесия граничных элементов выполняются. Так как все уравнения равновесия и условия закрепления выполняются, то решение точное.

Решение задачи изгиба свободно опертой по краям пластины при произвольной нагрузке методом Бубнова-Галеркина

Пусть имеется распределенная по поверхности пластины нагрузка р. Для этого случая решение ищем в виде ряда:

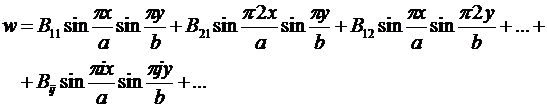
Подставляя в уравнение Софи-Жермен, получим:

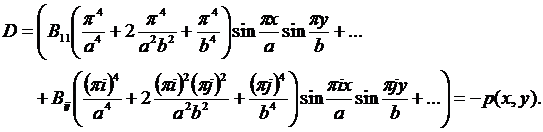
Для получения алгебраических уравнений относительно В₁₁, В₂₂… можно использовать любые методы (например, коллокаций), но наиболее удобным является метод, который является по сути методом Бубнова-Галеркина, и который в нашем случае сразу дает выражения для B_ij.

Умножим уравнение на 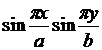, проинтегрируем по площади пластины:

.

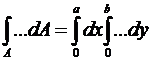Справа получим: .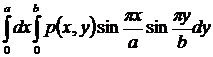

Рассмотрим левую часть:

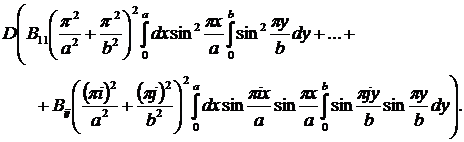
Оказывается, все слагаемые, кроме первого, равны нулю, причем

.

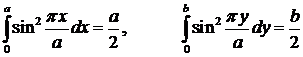Таким образом, из уравнения Софи-Жермен получаем:

.

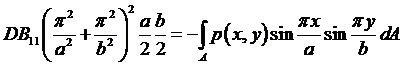Отсюда:

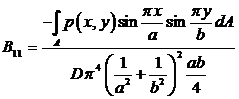
Аналогично находим:

.

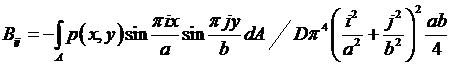Впервые это решение получил А.Навье.