Условия на границах пластины

Уравнение Софи-Жермен - это уравнение равновесия внутреннего элемента в виде 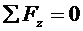. Кроме этого уравнения необходимо, чтобы выполнялись условия закрепления и уравнения равновесия граничных элементов на боковых кромках пластины (которые зависят от условий закрепления).

Если по краям пластина защемлена, то в явном виде можно записать только условия закрепления.

Рассмотрим защемленную пластину, изображенную на рис.14.6. Уравнения этих границ имеют следующий вид.

Левая граница: х = 0; правая: х = а;

передняя: у = 0; задняя: у = b.

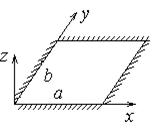
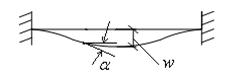
Рис.14.6 Рис.14.7

На границе должно быть:

w = 0.

Кроме того, на границах угол наклона должен быть равен нулю, т.е. a = 0(рис.14.7). Угол наклона на левой и правой границах определяется из соотношения tga=w¢_x. Так как a = 0, то на левой и правой кромках должно быть:

w¢_x=0.

Аналогично на передней и задней кромках должно быть:

w¢_у=0.

Если пластина шарнирно (свободно) оперта по краям, то на краю должно быть:

w = 0.

Для записи уравнения равновесия граничного элемента вырежем и рассмотрим граничный элемент (рис.14.9, 14.10). На него воздействует реактивная сила опоры R_xz. Поэтому касательные напряжения 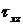компенсируются этой реактивной силой. Момент, образованный напряжениями 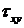, компенсируется реактивным моментом М_ху, лежащим в плоскости yz.

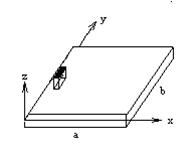
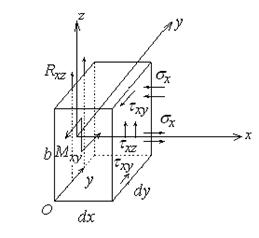
Рис.14.8

Рассмотрим другие уравнения равновесия. Из рисунка видно, что условие 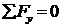удовлетворяется автоматически (т.к. при dx/dу → 0 на верхней и нижней гранях вклад касательных напряжений будет пренебрежим по сравнению с вкладом касательных напряжений 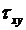). Уравнение 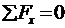также выполняется тождественно. Из уравнения 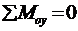следует соотношение:

.

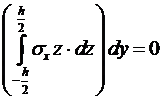Подставляя 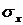по формуле (14.10), получим:

.

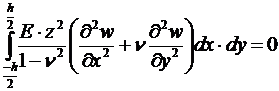Отсюда вытекает, что на грани х = 0 должно быть:

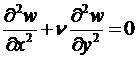(14.22)

Поскольку вдоль этой грани w = 0, то 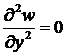. Тогда из (14.22) и из условия опирания для граничного элемента на краю х = 0 свободно опертой пластины имеем 2 условия:

.

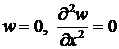Такие же условия должны выполняться на краю х = а.

Аналогично на краях у = 0 и у = b должны выполняться условия:

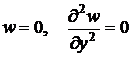. (14.23)

Случай незакрепленного края. Пусть край х = 0 загружен погонной силой 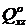и погонными моментами 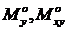(см. рис. 14.9-14.10). Условия равновесия граничного элемента для этого случая вызывали большие споры в течении многих лет. Впервые правильные уравнения были получены Кирхгоффом в 1850г.

Рассмотрим элемент, подобный рассмотренному в предыдущем случае (рис. 14.9-14.10).

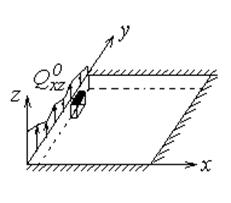
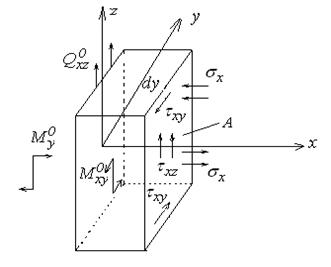
Рис.14.9 Рис.14.10

Также аналогично предыдущему можно увидеть, что уравнения равновесия 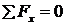, 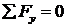удовлетворяются автоматически. Остаются следующие:

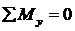, (14.24)

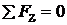, (14.25)

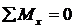, (14.26)

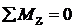. (14.27)

Первое уравнение дает (см. предыдущий случай):

.

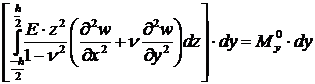Отсюда, сокращая на dy, получаем:

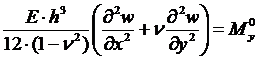. (14.28)

Рассмотрим уравнение (14.25).

Так как выражение для t_xz содержит z, (то есть t_xz переменна по высоте), то его равнодействующую искать простым умножением на площадь недопустимо. Поэтому разбиваем площадь А на элементарные площадки dA (рис.14.11), на каждой из них находим равнодействующую t_xz и, суммируя, получим силу :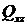

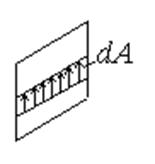
Рис.14.11

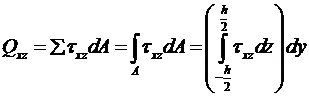. (14.29)

Подставляем этот результат в уравнение равновесия (14.25):

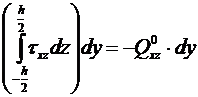. (14.30)

Здесь на 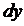можно сократить.

Из третьего уравнения (14.26) после аналогичных рассуждений вытекает соотношение:

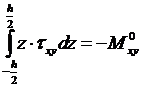. (14.31)

Если удовлетворено уравнение (14.30), то уравнение (14.31) может быть выполнено разве что случайно, т.е. обычно оно не может быть удовлетворено и наоборот. Можно эти два последних уравнения удовлетворить приближенно (т.е. в среднем). Например, из условия минимума невязки этих уравнений. Однако, как показал Кирхгофф (1850 г.), из закона сохранения энергии следует другой вариант приближенного удовлетворения этих уравнений, а именно, соотношение вида:

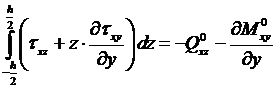. (14.32)

Лишь спустя 17 лет лорд Кельвин в 1867 году дал наглядное объяснение такому способу удовлетворения уравнений равновесия граничного элемента.

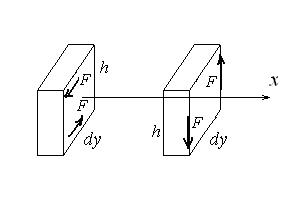
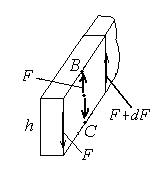
Рис.14.12 Рис.14.13

Подсчитаем момент относительно оси х, который создается напряжениями t_xy на элементе ширины dy (ось х проходит через центр тяжести грани элемента по нормали к этой грани):

.

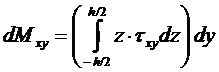Заменим его парой сил 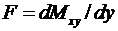с плечом dy, как это изображено на рис.14.12. Кельвин предложил далее заменить эту пару горизонтальных сил парой вертикальных сил (рис.14.12).

На соседнем элементе эти силы будут отличаться мало, а именно на величину dF.

Если после этого рассмотреть два соседних элемента, то увидим картину, изображенную на рис.14.13.

Видно, что силы 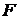на общей средней линии ВС компенсируются и остается лишь 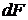. Расписывая 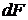, получим:

.

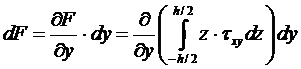Поделив на dy, получим вместо момента М_xy погонную вертикальную силу

.

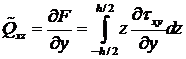Аналогично внешний погонный момент 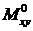можно заменить погонной вертикальной силой:

.

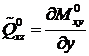Следовательно, система сил, 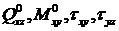, действующая на наш элемент, эквивалентна системе только вертикальных сил .

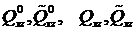Таким образом, получим для граничного элемента на кромке х = 0 уравнение 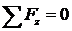в виде (14.32).

Аналогично, на кромке у = 0 уравнение равновесия (14.25) примет вид:

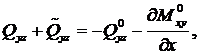
где

.

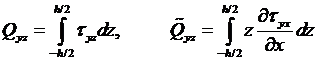Выражая напряжения через прогиб по формулам (14.10) и (14.17), условия равновесия на незакрепленных кромках можно записать следующим образом.

На незакрепленном краю х = 0 (или х = а):

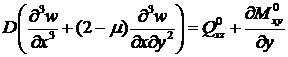. (14.33)

На незакрепленном краю у = 0 (или у = b):

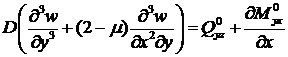. (14.34)

Здесь 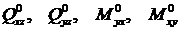- заданные на кромках внешние погонные поперечные силы и моменты (рис. 14.10).