Теорема о минимуме потенциальной энергии упругой системы и ее применение для Опосредованной оценки точности решения

Для сравнительной оценки решений различными методами применяют следующий подход. Вычисляют потенциальную энергию системы:

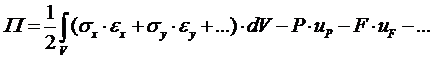, (9.1)

Здесьпервое слагаемое – энергия деформации тела, 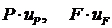– работы внешних сил Р и F на перемещениях 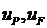элементов, к которым приложены эти силы.

Если окажется, что одно решение дает П₁, а второе П₂, причем П₁>П₂, то скорее всего второе решение-более точное. Это утверждение основано на следующей теореме.

Теорема. Потенциальная энергия системы (9.1) принимает минимальное значение для истинных перемещений, деформаций и напряжений.

Для простоты доказательство приведем для простейшего случая одномерной задачи.

Пусть известно точное решение:

u = u^точное,

тогда:

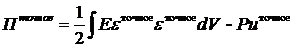. (9.2)

Приближенное решение представим в виде:

u = u^точное + Δu.

Следовательно,

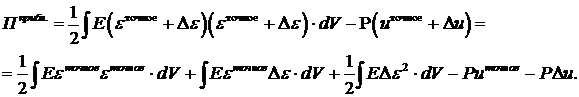
Учитывая (9.2), получим:

.

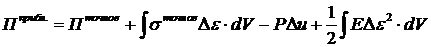В силу принципа возможных перемещений:

.

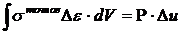В результате получаем:

.

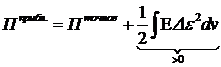Здесь второе слагаемое в правой части - сугубо положительная величина. Таким образом, для точного решения 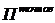всегда меньше, чем потенциальная энергия для приближенного решения.

Примечание.При оценке прочности логично называть более близким к точному то решение, которое ближе по максимальным напряжениям, под которым понимается обычно эффективное напряжение 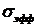(его называют также эквивалентным или приведенным). Для плоской задачи, например, согласно четвертой теории прочности:

.

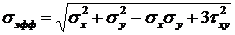Теорема не гарантирует того, что если П₁>П₂, то второе решение даст значение (s_эфф)_мах, которое будет ближе к точному.

Задача Фламана

Рассмотрим задачу воздействия погонной силы Р на полубесконечное упругое тело.

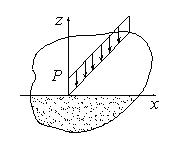
Рис.10.1

Это, например, расчетная схема давления на грунт ленточного фундамента.

Решение для этой задачи имеет вид:

.

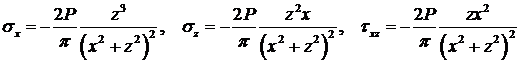Проверяя уравнения равновесия (за исключением линии действия силы Р) для плоской задачи при q_х = q_z = 0, удостоверяемся, что оно удовлетворяется везде. Отметим также тот известный факт, что в линейной теории упругости решение единственно.

Проведем анализ решения.

При приближении к точкам приложения погонной силы P, (т.е. при 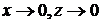) получаем, что .

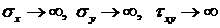Это означает, что вблизи точек приложения погонной силы P использовать решение для расчета на прочность бессмысленно. Однако как выяснится ниже, эти решения подобного типа можно использовать для определения поля напряжений при воздействии нагрузки, распределенной по площади.

Исследуем вопрос о том, как можно применить решение задачи Фламана в задаче о действии внешнего давления в плоской задаче. Для этого рассмотрим действие давления q(x) на полупространство (рис.10.2). То, что q не зависит от у означает, что оно не меняется в направлении Оу.

Найдем 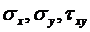. Возьмем площадку dξ на расстоянии ξ от начала координати перейдем от распределенной нагрузки к сосредоточенной силе dP= q dξ. Получаем задачу Фламана. Как известно, при переносе начала координат влево на расстояние ξ любая функция f записывается в виде:

f(х - ξ).

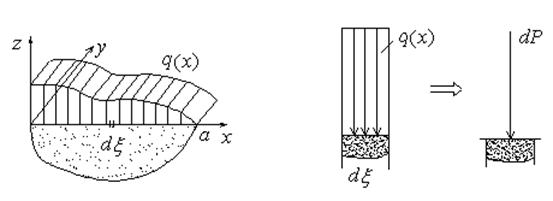
Рис.10.2 Рис.10.3

Тогда для силы dP решение можно записать в виде:

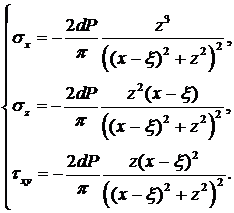
Такие же решения получим для других отрезков dξ, расположенных в других местах. Общее воздействие получим, суммируя напряжения от воздействия различных dP:

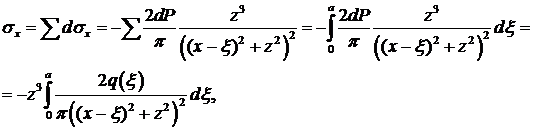
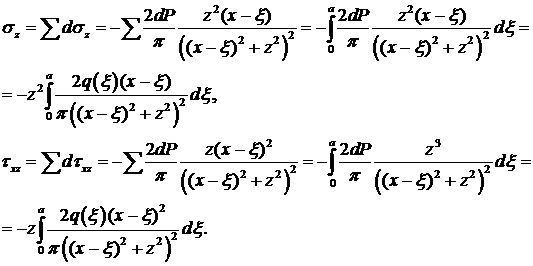Пример. Пусть q = const = q_o, а = 1. Тогда интегрируя, получим

.

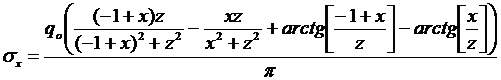Аналогично можно найти .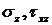

В этом случае бесконечных напряжений под нагрузкой не возникает (например, посередине при х=0.5 получим σ_х = 0.8183 q₀). Поэтому при расчете ленточных фундаментов вместо сосредоточенной силы необходимо задавать нагрузку q(х), близкую к реальному распределенному давлению на основание.