Некоторые методы приближенного решения задач теории упругости. Метод коллокаций
В общем случае задача определения напряженно-деформированного состояния может быть сведена к отысканию полей перемещений  . Приведем этапы решения задач теории упругости на примере плоской задачи.
. Приведем этапы решения задач теории упругости на примере плоской задачи.
1. Перемещения задаются в виде аппроксимаций с неизвестными (искомыми) коэффициентами. Например:
2.
 (4.1)
(4.1)
3. Записываются выражения для деформаций:
4.
 (4.2)
(4.2)
5. Находят выражения для напряжений. Например, в случае ПНС имеем:
 (4.3)
(4.3)
6. Соотношения (4.1) подставляются в условия закрепления, а напряжения - в уравнения равновесия. Получается система уравнений, которая содержит искомые коэффициенты, а также функции х, у, х2, у2.
7. Выбирается какой-либо метод, который позволяет исключить х, у и их функции из полученной системы, а также получить столько алгебраических уравнений, сколько имеется неизвестных констант в (4.1).
Рассмотрим, например, метод простых коллокацийв задаче орастяжении балки-стенки. Пусть известно, что
qx = 2x2, pх = 5, n = 0.

Рис.4.1
Решение:
Видно, что σу в нашей задаче можно принять равным нулю, так как n=0. Также отсутствуют и сдвиги τху = 0.
Получаем уравнение равновесия для внутреннего элемента 1 в виде:
 . (4.4)
. (4.4)
Уравнение равновесия для граничного элемента 2 при х=2 дает
 . (4.5)
. (4.5)
Выбираем  в виде:
в виде:
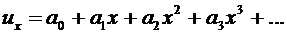
Ограничимся в дальнейшем кубическим полиномом.
Запишем условия закрепления при х = 0:
 .
.
Отсюда вытекает, что
 .
.
Далее выражаем деформацию  и напряжение
и напряжение  через
через  :
:
 (4.6)
(4.6)
Подставляя в уравнения равновесия (4.8), (4.9) получаем
 , (4.7)
, (4.7)
 . (4.8)
. (4.8)
Согласно методу коллокаций, для получения алгебраической системы выберем некоторые малые элементы с координатами х1, х2, … Уравнения равновесия будем выполнять только для них. Эти элементы (или точки) называются элементами (или точками) коллокации.
Пусть х1= 0, х2= 1. Тогда уравнение равновесия (4.7) дает:
 ,
,
 .
.
Отсюда:
 .
.
Из уравнения равновесия (4.12) граничного элемента получаем:
 .
.
Отсюда:

Таким образом:

Построим эпюру напряжений по длине (рис.4.2).


Рис.4.2 Рис.4.3
Отметим некоторые недостатки метода коллокаций.
Если брать число искомых коэффициентов не очень большим (2¸3), то решение сильно зависит от точек коллокации. Например, рассмотрим второй вариант точек коллокации, когда 
 .
.
При х1 =0 уравнение (4.11) дает:
 .
.
При х2 =0,5 из (4.11) получаем:

Из уравнения равновесия (4.12) граничного элемента вытекает:

Теперь решение принимает вид:
 .
.
Эпюра напряжений примет вид, изображенный на рис.4.2. Видно, что по максимальному напряжению отличие составляет 23%.
Для устранения этого недостатка применяют метод переопределенных коллокаций.Суть его в том, что число точек коллокаций берут так, чтобы число уравнений получилось больше числа неизвестных.
Составим систему уравнений равновесия, обозначив через Н полученную матрицу, через а – искомый вектор. Пусть число уравнений равно  , а число неизвестных равно
, а число неизвестных равно  . Уравнения равновесия представим в матричной форме:
. Уравнения равновесия представим в матричной форме:


Введем вектор невязки:

Вычислим его длину. Для этого используем формулу для скалярного умножения. В матричных обозначениях можно записать так:
 .
.
 называется квадратичной невязкой. Потребуем, чтобы он был минимален. По теореме Ферма должно быть:
называется квадратичной невязкой. Потребуем, чтобы он был минимален. По теореме Ферма должно быть:
 .
.
Дифференцируя выражение для квадратичной невязки получаем:
 .
.
Отсюда вытекает окончательное уравнение для определения а:
 .
.
Метод Бубнова-Галеркина
Рассмотрим его суть на предыдущем примере. Как и в методе коллокаций решение ищется в виде аппроксимации (4.5) с неизвестными коэффициентами, то есть:
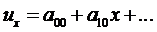 . (5.1)
. (5.1)
Аналогично по формулам (4.6), (4.7) находятся деформации и напряжения 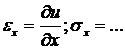 . Напряжения подставляются в уравнения равновесия внутреннего и граничных элементов, перемещения подставляются в условия закрепления. В результате снова получаем не алгебраические, а следующие функциональные уравнения.
. Напряжения подставляются в уравнения равновесия внутреннего и граничных элементов, перемещения подставляются в условия закрепления. В результате снова получаем не алгебраические, а следующие функциональные уравнения.
Уравнения равновесия внутреннего элемента типа (4.11):
F(a00, …, х) = - q(x). (5.2)
Уравнения равновесия граничных элементов типа (4.12):
H (a00,…, l) = p(l). (5.3)
Условия закрепления типа (4.13):
G (a00, …, 0) = 0. (5.4)
После этого начинаются различия в методах коллокаций и Бубнова-Галеркина. Слева и справа в уравнениях (5.2) функции равны или близки друг к другу, значит, и интегралы от них должны быть близки, т.е.:
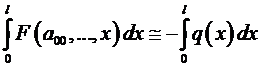 .
.
Исходные уравнения можно умножать на любую функцию j(х), от этого равенство не изменится. После этого можно проинтегрировать еще раз:
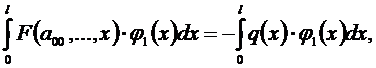
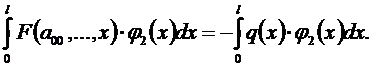
Добавляя уравнения (5.3), (5.4), в итоге получим столько уравнений, сколько неизвестных.
Недостаток метода в том, что 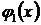 ,
, 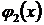 … выбираются расчетчиком, следовательно, решение достаточно субъективно. Однако, как правило, наилучшее приближение к точному решению получается тогда, когда в качестве
… выбираются расчетчиком, следовательно, решение достаточно субъективно. Однако, как правило, наилучшее приближение к точному решению получается тогда, когда в качестве 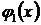 ,
, 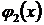 … принимаются функции, использованные для аппроксимации перемещений.
… принимаются функции, использованные для аппроксимации перемещений.
Рассмотрим пример, приведенный на рис.4.1.
Сначала интегрируем уравнение (4.11), а затем интегрируем его же, но умножив на 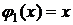 :
:
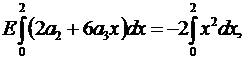 (5.4)
(5.4)
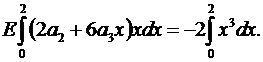 (5.5)
(5.5)
Уравнение для граничного элемента (4.12) и условие закрепления (4.13) останутся такими же:
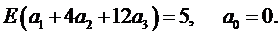 (5.6)
(5.6)
Интегрируя (5.4), (5.5) получаем:
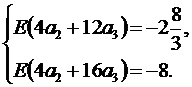
Вычитая из второго уравнения первое, получаем:
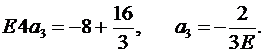
Из второго уравнения находим а2:
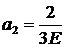 .
.
Из уравнения (5.6) находим а1:
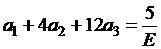 ,
, 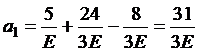 .
.
Таким образом,
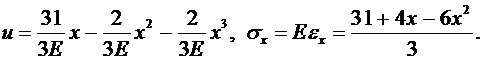
Эпюра напряжений имеет вид, приведенный на рис.5.1, и не очень сильно отличается от эпюры, приведенной на рис.4.2.
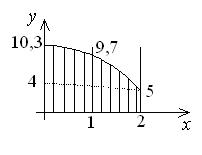
Рис.5.1.
МЕТОД РЭЛЕЯ-РИТЦА
Запишем соотношение, которое называется принципом возможных (виртуальных) перемещений. В простейшем случае одноосного растяжения оно имеет вид:
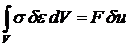 .
.
Рассмотрим случай наличия поверхностных сил.
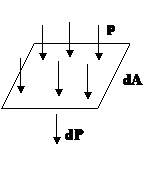 | Возьмем бесконечно малую площадку dA. Тогда: 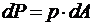 . Работа силы: . Работа силы: 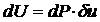 . Работа всех бесконечно малых сил dP: . Работа всех бесконечно малых сил dP: 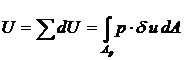 . . |
Рассмотрим случай наличия объемных сил.
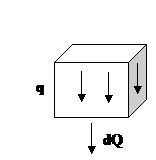 | Найдем равнодействующую 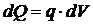 . Она совершит работу . Она совершит работу 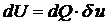 . В результате работа объемных сил: . В результате работа объемных сил: 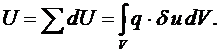 |
Таким образом, в общем случае принцип возможных перемещений примет вид:
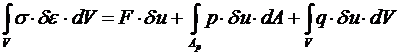 . (6.1)
. (6.1)
Аналогично можно рассмотреть случай, когда действуют еще и касательные напряжения. Тогда к энергии деформации добавится следующее слагаемое:
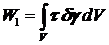 .
.
Здесь t - касательное напряжение, g - сдвиг малого элемента. Тогда принцип возможных (виртуальных ) перемещений примет вид:
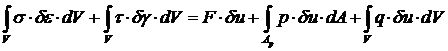 .
.
Эта запись справедлива и в векторной форме, если под 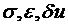 подразумевать векторы.
подразумевать векторы.
Суть метода Рэлея-Ритца заключается в следующем. Как и в методе коллокаций, или Бубнова-Галеркина перемещения представляются в виде аппроксимации с неизвестными коэффициентами. Как и ранее, пояснения идут на примере простейшей одномерной задачи. Выбираем 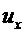 , например, в виде:
, например, в виде:
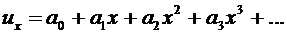 .
.
Зададим условия закрепления при х = 0:
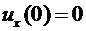 .
.
Отсюда вытекает, что
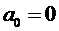 .
.
Далее выражаем деформацию и напряжение через 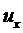 :
:
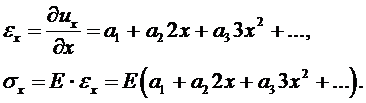 (6.2)
(6.2)
Подставим напряжение в правую часть принципа возможных перемещений (6.1). Далее выбираем несколько возможных (виртуальных, т.е. воображаемых) перемещений 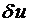 , через которые находим
, через которые находим 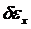 по соотношениям Коши:
по соотношениям Коши:
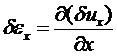 .
.
Количество разных воображаемых перемещений выбираем равным количеству неизвесных коэффициентов 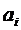 , чтобы число неизвестных было равно числу уравнений. После этого проводится интегрирование соотношений (6.1). Это дает систему обыкновенных линейных алгебраических уравнений для коэффициентов
, чтобы число неизвестных было равно числу уравнений. После этого проводится интегрирование соотношений (6.1). Это дает систему обыкновенных линейных алгебраических уравнений для коэффициентов 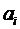 .
.
Основное достоинство метода состоит в том, что в отличие от метода Бубнова-Галеркина здесь не требуется выполнять условие равновесия граничных элементов, что позволяет использовать аппроксимации с меньшим количеством неизвестных.
Рассмотрим пример, приведенный на рис. 4.6 с теми же данными, что и ранее, т.е. при qx = 2x2, pх = 5. Примем следующую аппроксимацию для перемещений:
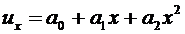 . (6.3)
. (6.3)
Снова из условия закрепления 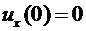 вытекает, что
вытекает, что
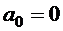 .
.
Далее выражаем деформацию и напряжение через 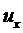 :
:
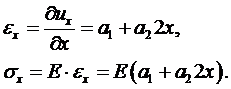 (6.4)
(6.4)
Теперь выберем два разных 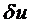 . Для этого применяют следующий подход. В первом варианте положим в аппроксимации (6.3) значения а1=1, а2=0. Тогда получим:
. Для этого применяют следующий подход. В первом варианте положим в аппроксимации (6.3) значения а1=1, а2=0. Тогда получим:
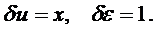 (6.5)
(6.5)
Подставим (6.4), (6.5) в (6.3), в результате получим:
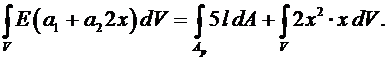 (6.5)
(6.5)
Представим объем 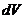 в виде объема тонкого диска толщины dx. Тогда получим:
в виде объема тонкого диска толщины dx. Тогда получим:
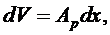
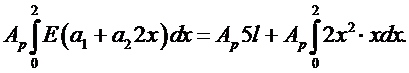
Отсюда вытекает первое уравнение в виде:
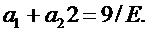 (6.6)
(6.6)
Во втором варианте положим в аппроксимации (6.3) значения а1=0, а2=1. Тогда получим:
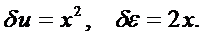 (6.7)
(6.7)
Подставим (6.7), (6.4) в (6.3):
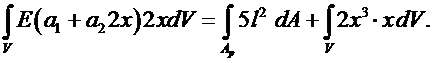 (6.8)
(6.8)
Аналогично предыдущему получим:
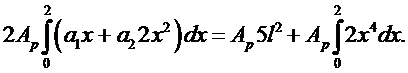
Отсюда вытекает второе уравнение в виде:
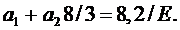 (6.9)
(6.9)
Решение системы (6.6), (6.9) дает значения:

Напряжение будет вычисляться по формуле (6.4):
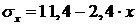 .
.
В заделке напряжение будет
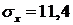 .
.
На правом торце 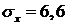 .
.
Метод конечных разностей
Суть метода изложим для случая плоской задачи. Уравнения равновесия для внутреннего элемента имеют вид:

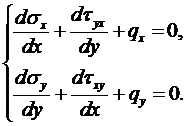
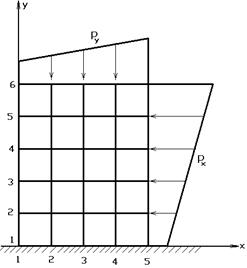
Рис.7.1
Для граничных элементов в случае, например, изображенном на рис.7.1, уравнения равновесия примут вид:
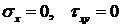 при
при 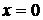 ,
,
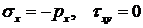 при
при 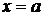 ,
,
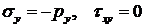 при
при 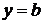 .
.
В методе конечных разностей искомыми считаем не функции 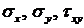 , а их значения во внутренних и граничных узлах.
, а их значения во внутренних и граничных узлах.
Нумерация неизвестных осуществляется с помощью двух индексов, например, 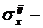 это значение функции
это значение функции 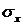 в i-й строчке, в j - м столбце.
в i-й строчке, в j - м столбце.
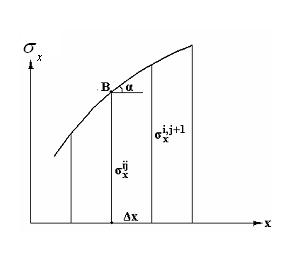
Рис.7.2
Воспользуемся геометрическим смыслом производной (это тангенс угла наклона касательной к кривой). Из рис.7.2 видно, что в точке с индексами i j имеем:
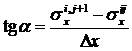 .
.
Следовательно,
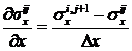 .
.
Таким образом, производная выражается через искомые значения функции 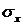 .
.
Аналогично поступают с другими неизвестными функциями, т.е. с  . Все это подставляют в уравнения равновесия. В результате получаем систему линейных алгебраических уравнений относительно значений напряжений
. Все это подставляют в уравнения равновесия. В результате получаем систему линейных алгебраических уравнений относительно значений напряжений 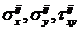 .
.
Рассмотрим пример, приведенный на рис. 7.3.
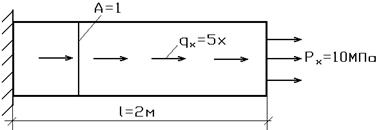
Рис.7.3
Рассмотрим задачу отыскания 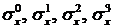 в точках с координатами:
в точках с координатами:
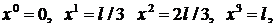
Эти величины найдем из условий равновесия:
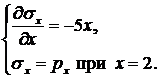
Для граничного элемента получаем 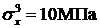 .
.
Для внутренних элементов:
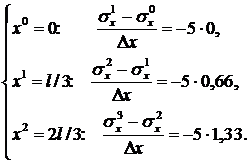
Получилось 3 уравнения с 3-я неизвестными. Учитывая, что 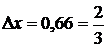 , получим:
, получим:
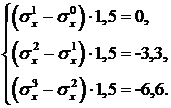
Из третьего уравнения с учетом того, что 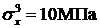 , найдем:
, найдем:
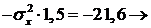
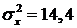
Из второго и первого уравнений вытекает, что
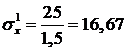 ,
, 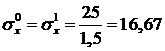 .
.
К недостатку метода можно отнести то, что в случае плоской задачи, если область не прямоугольная, трудно записываются уравнения равновесия граничных элементов.
Достоинства метода заключаются в следующем.
1) Сразу получаем значения искомых функций
2) Легко следить за сходимостью метода при увеличении числа неизвестных.
Метод конечных элементов
МКЭ вобрал в себя положительные стороны и МКР, и метода Рэлея-Ритца. МКЭ основан на законе сохранения энергии, записанного в форме принципа виртуальных перемещений. Суть МКЭ заключатся в следующем.
1. Тело представляют в виде набора элементов с объемами 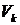 :
:
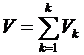 .
.
2. В каждом элементе 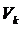 аппроксимируют искомые перемещения:
аппроксимируют искомые перемещения:
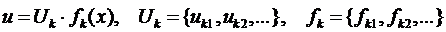 ,
,
здесь 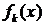 – выбираемые расчетчиком вектор известных функций,
– выбираемые расчетчиком вектор известных функций, 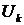 - вектор искомых узловых перемещений.
- вектор искомых узловых перемещений.
Наборы функций 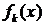 на сегодня имеются в большом количестве.
на сегодня имеются в большом количестве.
3. На каждом элементе вычисляется работа внешних сил и накопленная упругая энергия элемента.
4. Все это подставляется в закон сохранения, например, в принцип возможных перемещений. В качестве 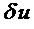 берутся какие-либо возможные перемещения. Обычно в качестве них берут соотношения
берутся какие-либо возможные перемещения. Обычно в качестве них берут соотношения 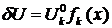 , но с заданными значениями узловых перемещений
, но с заданными значениями узловых перемещений 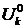 . При этом для получения систем уравнений применяют следующую процедуру. Сначала принимают
. При этом для получения систем уравнений применяют следующую процедуру. Сначала принимают 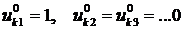 , далее берут
, далее берут 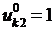 все остальные равны нулю и т.д.
все остальные равны нулю и т.д.
В результате получим столько уравнений, сколько неизвестных.
Рассмотрим пример расчета бруса, приведенного на рис.8.1.
Пусть известно, что Р0=25 МПа; q=x2 МПа; l=3м. Найти перемещения узлов1,2 (т.е. u1, u2).
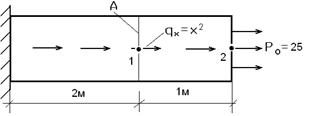
Рис.8.1
Разобьем стержень на два элемента – первый длиной 2 м, второй длиной 1 м. На каждом из них аппроксимируем перемещения линейными зависимостями.
Рассмотрим первый элемент и аппроксимируем перемещение следующей линейной функцией:
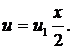
Тогда:
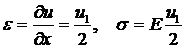 .
.
Рассмотрим второй элемент:
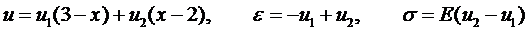 .
.
Подставим в закон сохранения (учитываем, что на правом торце 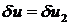 ):
):
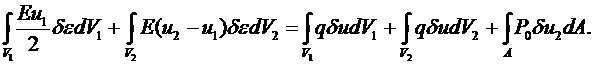
В качестве вариаций перемещений и деформаций (вооброжаемых перемещений и деформаций) примем:
1-й элемент: 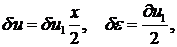
2-й элемент: 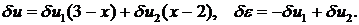
Полагая сначала 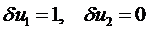 , получим первое уравнение:
, получим первое уравнение:
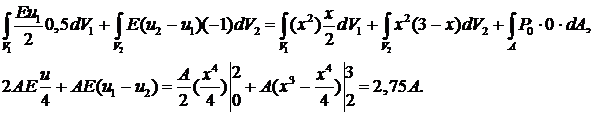
Полагая 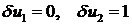 , получим второе уравнение:
, получим второе уравнение:
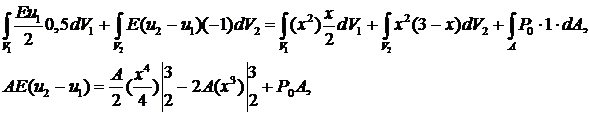
Таким образом, нашли систему уравнений относительно 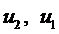 .
.
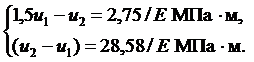
Выразим перемещение 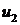 из второго уравнения:
из второго уравнения:
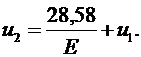
Из первого уравнения тогда находим:
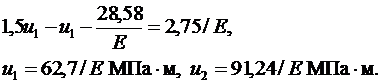
Теперь можно вычислить напряжения:
1 элемент: 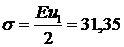 МПа, 2 элемент:
МПа, 2 элемент: 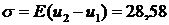 МПа.
МПа.
Достоинства метода
1. Решение сразу дает значения перемещений узлов упругого тела.
2. Легко проверяется сходимость метода при сгущении сетки.
3. Матрица системы уравнений получается симметрической и ленточной. Это позволяет экономить память ЭВМ и ускорять процесс решения.
4. В этом методе необходимо выполнять только геометрические граничные условия, например, задавать равными нулю перемещения закрепленных узлов. А записывать уравнение равновесия граничных и внутренних элементов как в методе Бубнова не нужно, поскольку закон сохранения энергии полностью эквивалентен этим уравнениям равновесия.
Недостатки метода
Распределение напряжений получается негладким. Для получения гладкого распределения напряжения существуют разные подходы. Наиболее часто применяемым является простейший метод осреднения напряжений в узлах (но он является наименее точным).
Приведем метод конечных элементов в матричной форме. Сначала проводится разбивка на элементы. Задача заключается в нумерации элементов, узлов и записи их связей.
Запись осуществляется в виде матрицы топологии, например, в виде:
[М] = [элементы, номера узлов]
М = 
Далее вводится аппроксимация перемещений на элементе.
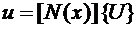 .
.
N – матрица, которая зависит от координат, {U} – вектор, составленный из перемещений узлов элемента, он является искомым.
Формы матрицы N на сегодня разработаны и имеются во всех пакетах МКЭ.
Например, в рассмотренной выше задаче N имеет вид:
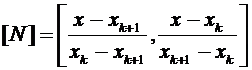 ,
,
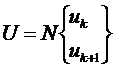 .
.
Далее вычисляются деформации по соотношениям Коши:
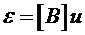 .
.
Тогда получим:
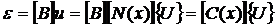 .
.
Затем записываем соотношения для напряжения по закону Гука.
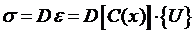 .
.
Выберем вариацию.
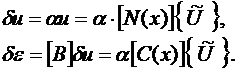
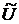 - воображаемый вектор узловых перемещений. Произвольность
- воображаемый вектор узловых перемещений. Произвольность 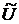 требуется согласно принципу Лагранжа.
требуется согласно принципу Лагранжа.
Подставим в принцип Лагранжа.
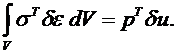
Здесь индексом Т обозначена операция транспонирования
Подставляя в принцип Лагранжа, получим:
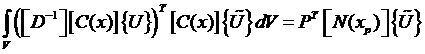 ,
,
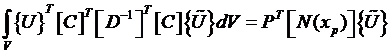 .
.
При интегрировании x, y, z исчезают. В результате получаем:
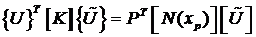 .
.
Здесь
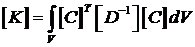 .
.
Матрица К называется матрицей жесткости.
Поскольку 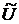 - произвольный вектор, то можно сначала положить
- произвольный вектор, то можно сначала положить
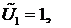
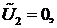
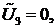 …
…
Тогда получим одно уравнение. Далее полагаем, что
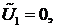
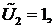
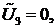 …
…
и получаем 2-е уравнение и т.д.
В результате получаем столько уравнений, сколько неизвестных. Эту систему можно записать в следующем виде:
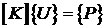 .
.
Решив эту систему уравнений, найдем перемещения каждого узла. После этого можно найти деформации и напряжения в элементах по соотношениям:
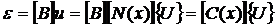 ,
,
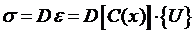 .
.
