Основы теории упругости и элементы теории пластин и оболочек: Учебное пособие / Р.А.Каюмов – Казань: Изд-во Казанск. гос. архитек.-строит. ун-та. 2016. 111 с.
Каюмов Р.А.
Основы теории упругости
И элементы теории
Пластин и оболочек
Казань
УДК 539.3
ББК
К 12
Каюмов Р.А.
Основы теории упругости и элементы теории пластин и оболочек: Учебное пособие / Р.А.Каюмов – Казань: Изд-во Казанск. гос. архитек.-строит. ун-та. 2016. 111 с.
ISBN 978-5-7829-0486-9
Табл. 0 Ил.32 Библиогр. 13 имен.
Печатается по решению Редакционно-издательского совета Казанского государственного архитектурного-строительного университета. Работа выполнена при поддержке Министерства образования и науки Российской Федерации, проект №1660 государственного задания в сфере научной деятельности по Заданию № 2014/58 за 2015
Учебное пособие содержит основные понятия, допущения и законы, применяемые в теории упругости, теории пластин и оболочек, некоторые методы решения задач.
Предназначено для направления подготовки 08.03.01 «Строительство» и специальности 08.05.01 «Строительство уникальных зданий и сооружений».
Рецензенты:
Д.ф.-м.н. профессор КГТУ имени А.Н.Туполева академик АН РТ В.Н. Паймушин
Д.ф.-м.н. профессор, заведующий кафедрой «Теоретическая механика и сопротивление материалов» КГТУ имени С.М. Кирова М.Н. Серазутдинов
УДК 539.3
ББК
| Ó Казанский государственный архитектурно-строительный университет, 2015 | |
| JSBN 978-5-7829-0486-9 | Ó Каюмов Р.А., 2015 |
Введение
Расчет конструкций можно условно разбить на 2 следующих этапа:
1) Определение напряженно-деформированного состояния конструкций.
2) Проверка ее прочности, жесткости и устойчивости.
В курсах сопротивления материалов и строительной механики этот расчет ведется для элементов конструкций, изготовленных из стержней. Теория же упругости – это наука, которая занимается вопросами определения напряженно-деформированного состояния упругих тел произвольной конфигурации, в том числе характерных для строительства балок-стенок, плит, оболочек, стыковых узлов.
Статическая теория упругости использует следующие законы механики:
1. Уравнения равновесия:
∑ Fx=0, ∑ Fy=0, ∑ Fz=0, ∑ Mx=0, ∑ My=0, ∑ Mz=0.
2. Закон Гука, который предполагает прямо пропорциональную зависимостьдеформаций от нагрузок. Из курса сопротивления материалов известны следующие соотношения обобщенного закона Гука:
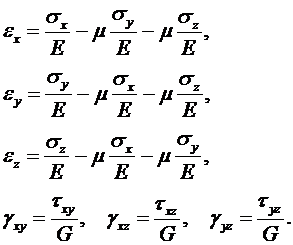
3. Закон Дюгамеля-Неймана (закон линейного температурного расширения):
εx = εу = εz = α∙∆T.
Уравнения равновесия
Типы плоских задач теории упругости
Существует два типа плоских задач, описывающих два типа напряженно-деформированного состояния:
- плоское напряженное состояние (ПНС);
- плоское деформированное состояние (ПДС).
КИНЕМАТИЧЕСКИЕ СООТНОШЕНИЯ
Рассмотрим деформацию балки-стенки под действием некоторой нагрузки.
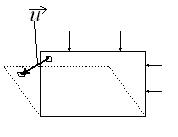
Рис.2.1
Введем вектор перемещений 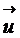 малого элемента (рис.2.1). Так как разные элементы перемещаются по-разному, то
малого элемента (рис.2.1). Так как разные элементы перемещаются по-разному, то 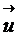 зависит от координат элемента (его положения), т.е.
зависит от координат элемента (его положения), т.е. 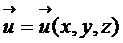 . Согласно закону параллелограмма, мы можем рассматривать не вектор, а его компоненты:
. Согласно закону параллелограмма, мы можем рассматривать не вектор, а его компоненты:
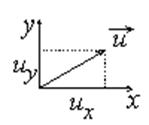
Рис.2.2.
Зная перемещения, можно найти деформации малых элементов тела. Правила их вычисления даютсоотношения Коши.
Соотношения Коши
Рассмотрим малый элемент и его перемещение (рис.2.3). Найдем формулы для вычисления деформаций через ux, uy . Пусть точка С перемещается в точку С¢. Тогда 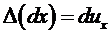 .
.
Отсюда относительная линейная деформация (иногда ее называют осевой)будет:
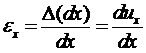 . (2.1)
. (2.1)
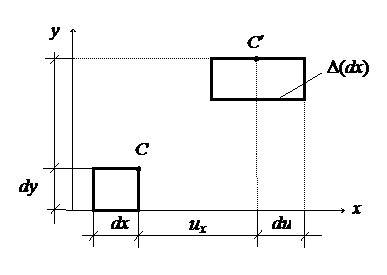
Рис.2.3
Это первое соотношение Коши. Аналогично:
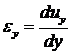 .
.
Рассмотрим сдвиг нашего элемента. Пусть точка В перешла в В¢ (рис.2.4).
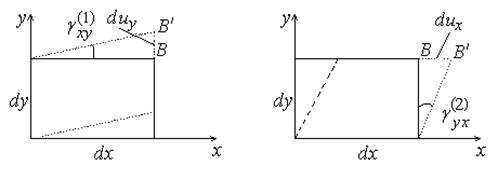
Рис.2.4. Рис.2.5.
В силу малости угла 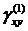 имеем:
имеем:
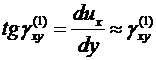 .
.
Отметим, что даже при 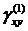 =300 погрешность составляет около 5%. Точно так же находим, что:
=300 погрешность составляет около 5%. Точно так же находим, что:
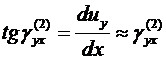 .
.
Суммарное изменение прямого угла будет:
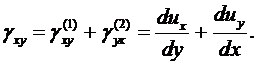 (2.2)
(2.2)
Этот угол называют деформацией сдвига (иногда углом сдвига), а соотношение (2.2) – вторым соотношением Коши.
Для краткости в дальнейшем в плоской задаче иногда индексы у угла 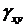 будем опускать.
будем опускать.
Задача о дамбе
Поскольку при оценке прочности обычно необходимо знать лишь напряженное состояние тела, то интерес представляют задачи, в которых удается ограничиться только уравнениями равновесия. Одной из таких является, например, задача о дамбе (рис.3.1). Уравнение линии ВD имеет вид:
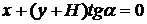 . (3.1)
. (3.1)
Давление воды увеличивается с глубиной по закону:
pх = - p0 ∙(Н-у)/м; р0=0.1 кг/см2. (3.2)



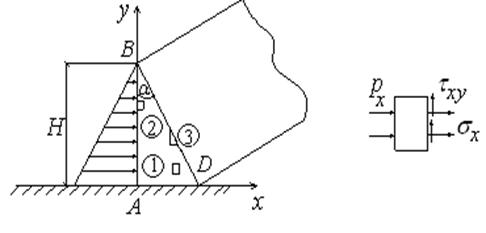
Рис.3.1 Рис.3.2
Считается, что дамба находится в плоском деформированном состоянии. Тогда уравнения равновесия внутреннего элемента имеют вид:
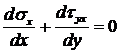 , (3.3)
, (3.3)
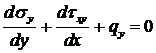 . (3.4)
. (3.4)
Для простоты в дальнейшем силой веса 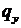 дамбы пренебрежем.
дамбы пренебрежем.
Решение ищем в виде:
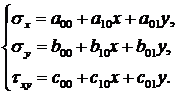 (3.5)
(3.5)
Необходимо определить коэффициенты aij; bij; cij .
Из уравнений равновесия внутреннего элемента 1 получаем:
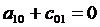 - первое уравнение равновесия внутреннего элемента;
- первое уравнение равновесия внутреннего элемента;
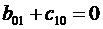 - второе уравнение равновесия внутреннего элемента.
- второе уравнение равновесия внутреннего элемента.
Отсюда:
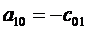 , (3.6)
, (3.6)
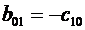 . (3.7)
. (3.7)
Из уравнений равновесия элемента 2 на левой грани (его координаты: х = 0, у – любое) вытекает (рис 3.3):
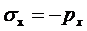 , (3.8)
, (3.8)
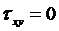 . (3.9)
. (3.9)
Подставляя сюда (3.3) и (3.5) получаем:
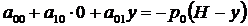 , 3.10)
, 3.10)
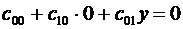 . (3.11)
. (3.11)
Сначала в качестве координат центра малого элемента 2 примем точку х=0, у=0. Тогда получим из (3.10), (3.11):
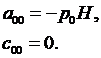
В качестве координат центра малого элемента 3 примем точку х=0, у=Н/2. Подставляя в (3.10) (3.11), получим:
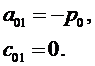
Из (3.6) тогда вытекает, что 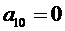
Из уравнения равновесия элемента 3 на наклонной грани (рис.3.1, рис.3.3) следует:
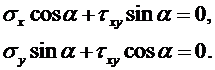
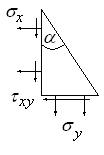
Рис. 3.3
Подставляя сюда (3.5) получаем:
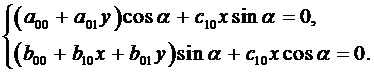 (3.12)
(3.12)
Учтем уравнение прямой BD:
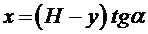 .
.
Тогда уравнения (3.12) примут вид:
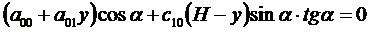 . (3.13)
. (3.13)
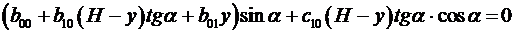 .(3.14)
.(3.14)
Выберем координаты центра этого элемента в виде:
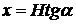 , у = 0.
, у = 0.
Тогда из уравнения (3.13) вытекает:
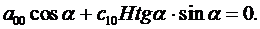 (3.15)
(3.15)
Наконец выбирая координаты центра третьего элемента в виде:
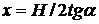 , у= H/2,
, у= H/2,
получаем из уравнения (3.13):
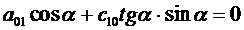 . (3.16)
. (3.16)
Из (3.15), (3.16) находим, что
с10=р0 сtg2α, а00= - р0Н.
Аналогично получаем систему уравнений для отыскания оставшихся неизвестных, подставляя в (3.14) координаты центра элемента, находящегося в вершине дамбы. Тогда решение запишется в виде:
b00=р0 Н сtg2α, b10= - р0 сtg3α, b01= - р0 сtg2α.
Подставляя все коэффициенты в (3.5), получим:
σх = р0 у,
σу = (- р0 сtg3α) х - (р0 сtg2α) у,
τху = (р0 сtg2α) х.
Выводы из решения
1. Решение имеет очень простой вид.
2. Это решение не может удовлетворить условия закрепления основания, а именно: условию eх=0 на линии АВ, поскольку после подстановки вычисленных значений напряжений по закону Гука получим:
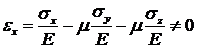 .
.
Если нас не интересует точность решения в опорной зоне, то решение приемлемо. Однако это противоречие не является существенным, так как условие жесткой заделки является лишь некоторой приближенной заменой реальных условий закрепления. Все недостатки решений такого рода сглаживаются введением коэффициента запаса.
Примечание. Как было отмечено ранее, кроме уравнений равновесия напряжения должны удовлетворять условию совместности деформаций (2.4). В нашем случае оно будет удовлетворяться тождественно, поскольку напряжения представляют собой линейные функции, а в соотношения (2.4) необходимо подставлять вторые производные.
Метод Бубнова-Галеркина
Рассмотрим его суть на предыдущем примере. Как и в методе коллокаций решение ищется в виде аппроксимации (4.5) с неизвестными коэффициентами, то есть:
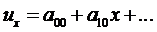 . (5.1)
. (5.1)
Аналогично по формулам (4.6), (4.7) находятся деформации и напряжения 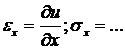 . Напряжения подставляются в уравнения равновесия внутреннего и граничных элементов, перемещения подставляются в условия закрепления. В результате снова получаем не алгебраические, а следующие функциональные уравнения.
. Напряжения подставляются в уравнения равновесия внутреннего и граничных элементов, перемещения подставляются в условия закрепления. В результате снова получаем не алгебраические, а следующие функциональные уравнения.
Уравнения равновесия внутреннего элемента типа (4.11):
F(a00, …, х) = - q(x). (5.2)
Уравнения равновесия граничных элементов типа (4.12):
H (a00,…, l) = p(l). (5.3)
Условия закрепления типа (4.13):
G (a00, …, 0) = 0. (5.4)
После этого начинаются различия в методах коллокаций и Бубнова-Галеркина. Слева и справа в уравнениях (5.2) функции равны или близки друг к другу, значит, и интегралы от них должны быть близки, т.е.:
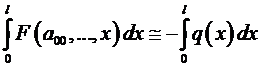 .
.
Исходные уравнения можно умножать на любую функцию j(х), от этого равенство не изменится. После этого можно проинтегрировать еще раз:
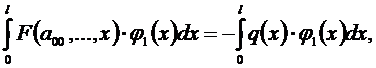
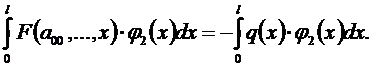
Добавляя уравнения (5.3), (5.4), в итоге получим столько уравнений, сколько неизвестных.
Недостаток метода в том, что 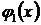 ,
, 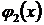 … выбираются расчетчиком, следовательно, решение достаточно субъективно. Однако, как правило, наилучшее приближение к точному решению получается тогда, когда в качестве
… выбираются расчетчиком, следовательно, решение достаточно субъективно. Однако, как правило, наилучшее приближение к точному решению получается тогда, когда в качестве 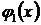 ,
, 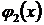 … принимаются функции, использованные для аппроксимации перемещений.
… принимаются функции, использованные для аппроксимации перемещений.
Рассмотрим пример, приведенный на рис.4.1.
Сначала интегрируем уравнение (4.11), а затем интегрируем его же, но умножив на 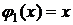 :
:
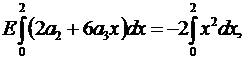 (5.4)
(5.4)
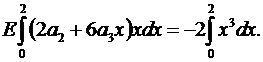 (5.5)
(5.5)
Уравнение для граничного элемента (4.12) и условие закрепления (4.13) останутся такими же:
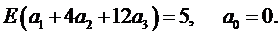 (5.6)
(5.6)
Интегрируя (5.4), (5.5) получаем:
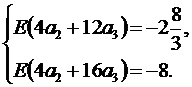
Вычитая из второго уравнения первое, получаем:
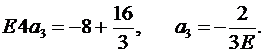
Из второго уравнения находим а2:
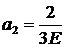 .
.
Из уравнения (5.6) находим а1:
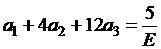 ,
, 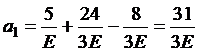 .
.
Таким образом,
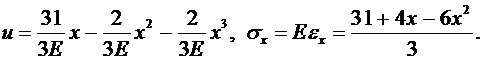
Эпюра напряжений имеет вид, приведенный на рис.5.1, и не очень сильно отличается от эпюры, приведенной на рис.4.2.
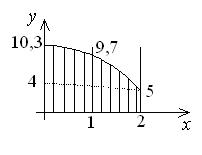
Рис.5.1.
МЕТОД РЭЛЕЯ-РИТЦА
Запишем соотношение, которое называется принципом возможных (виртуальных) перемещений. В простейшем случае одноосного растяжения оно имеет вид:
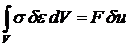 .
.
Рассмотрим случай наличия поверхностных сил.
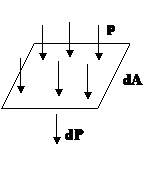 | Возьмем бесконечно малую площадку dA. Тогда: 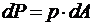 . Работа силы: . Работа силы: 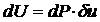 . Работа всех бесконечно малых сил dP: . Работа всех бесконечно малых сил dP: 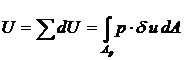 . . |
Рассмотрим случай наличия объемных сил.
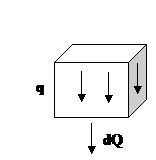 | Найдем равнодействующую 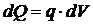 . Она совершит работу . Она совершит работу 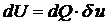 . В результате работа объемных сил: . В результате работа объемных сил: 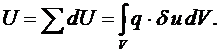 |
Таким образом, в общем случае принцип возможных перемещений примет вид:
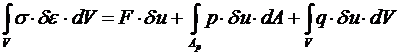 . (6.1)
. (6.1)
Аналогично можно рассмотреть случай, когда действуют еще и касательные напряжения. Тогда к энергии деформации добавится следующее слагаемое:
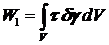 .
.
Здесь t - касательное напряжение, g - сдвиг малого элемента. Тогда принцип возможных (виртуальных ) перемещений примет вид:
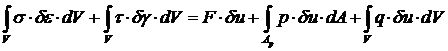 .
.
Эта запись справедлива и в векторной форме, если под 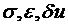 подразумевать векторы.
подразумевать векторы.
Суть метода Рэлея-Ритца заключается в следующем. Как и в методе коллокаций, или Бубнова-Галеркина перемещения представляются в виде аппроксимации с неизвестными коэффициентами. Как и ранее, пояснения идут на примере простейшей одномерной задачи. Выбираем 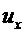 , например, в виде:
, например, в виде:
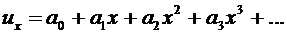 .
.
Зададим условия закрепления при х = 0:
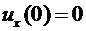 .
.
Отсюда вытекает, что
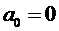 .
.
Далее выражаем деформацию и напряжение через 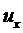 :
:
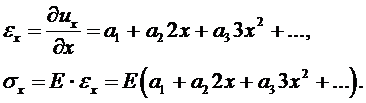 (6.2)
(6.2)
Подставим напряжение в правую часть принципа возможных перемещений (6.1). Далее выбираем несколько возможных (виртуальных, т.е. воображаемых) перемещений 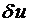 , через которые находим
, через которые находим 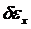 по соотношениям Коши:
по соотношениям Коши:
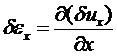 .
.
Количество разных воображаемых перемещений выбираем равным количеству неизвесных коэффициентов 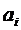 , чтобы число неизвестных было равно числу уравнений. После этого проводится интегрирование соотношений (6.1). Это дает систему обыкновенных линейных алгебраических уравнений для коэффициентов
, чтобы число неизвестных было равно числу уравнений. После этого проводится интегрирование соотношений (6.1). Это дает систему обыкновенных линейных алгебраических уравнений для коэффициентов 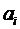 .
.
Основное достоинство метода состоит в том, что в отличие от метода Бубнова-Галеркина здесь не требуется выполнять условие равновесия граничных элементов, что позволяет использовать аппроксимации с меньшим количеством неизвестных.
Рассмотрим пример, приведенный на рис. 4.6 с теми же данными, что и ранее, т.е. при qx = 2x2, pх = 5. Примем следующую аппроксимацию для перемещений:
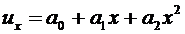 . (6.3)
. (6.3)
Снова из условия закрепления 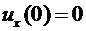 вытекает, что
вытекает, что
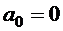 .
.
Далее выражаем деформацию и напряжение через 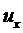 :
:
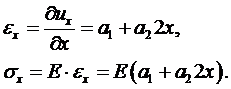 (6.4)
(6.4)
Теперь выберем два разных 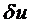 . Для этого применяют следующий подход. В первом варианте положим в аппроксимации (6.3) значения а1=1, а2=0. Тогда получим:
. Для этого применяют следующий подход. В первом варианте положим в аппроксимации (6.3) значения а1=1, а2=0. Тогда получим:
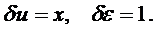 (6.5)
(6.5)
Подставим (6.4), (6.5) в (6.3), в результате получим:
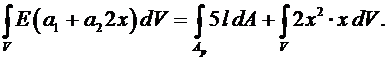 (6.5)
(6.5)
Представим объем 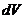 в виде объема тонкого диска толщины dx. Тогда получим:
в виде объема тонкого диска толщины dx. Тогда получим:
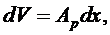
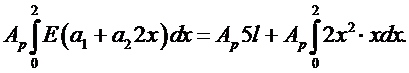
Отсюда вытекает первое уравнение в виде:
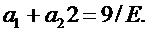 (6.6)
(6.6)
Во втором варианте положим в аппроксимации (6.3) значения а1=0, а2=1. Тогда получим:
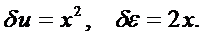 (6.7)
(6.7)
Подставим (6.7), (6.4) в (6.3):
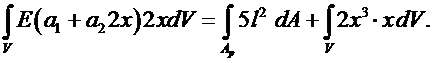 (6.8)
(6.8)
Аналогично предыдущему получим:
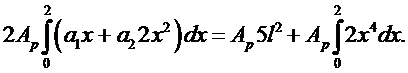
Отсюда вытекает второе уравнение в виде:
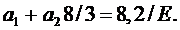 (6.9)
(6.9)
Решение системы (6.6), (6.9) дает значения:

Напряжение будет вычисляться по формуле (6.4):
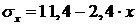 .
.
В заделке напряжение будет
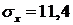 .
.
На правом торце 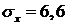 .
.
Метод конечных разностей
Суть метода изложим для случая плоской задачи. Уравнения равновесия для внутреннего элемента имеют вид:

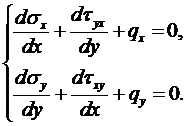
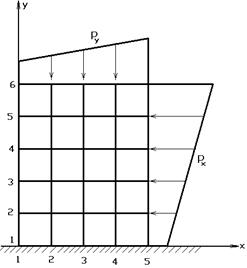
Рис.7.1
Для граничных элементов в случае, например, изображенном на рис.7.1, уравнения равновесия примут вид:
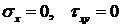 при
при 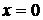 ,
,
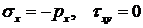 при
при 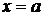 ,
,
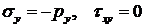 при
при 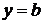 .
.
В методе конечных разностей искомыми считаем не функции 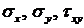 , а их значения во внутренних и граничных узлах.
, а их значения во внутренних и граничных узлах.
Нумерация неизвестных осуществляется с помощью двух индексов, например, 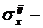 это значение функции
это значение функции 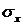 в i-й строчке, в j - м столбце.
в i-й строчке, в j - м столбце.
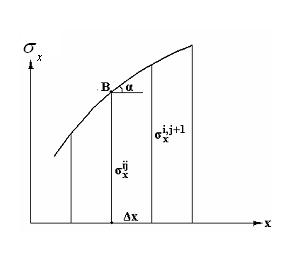
Рис.7.2
Воспользуемся геометрическим смыслом производной (это тангенс угла наклона касательной к кривой). Из рис.7.2 видно, что в точке с индексами i j имеем:
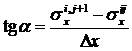 .
.
Следовательно,
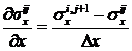 .
.
Таким образом, производная выражается через искомые значения функции 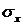 .
.
Аналогично поступают с другими неизвестными функциями, т.е. с 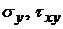 . Все это подставляют в уравнения равновесия. В результате получаем систему линейных алгебраических уравнений относительно значений напряжений
. Все это подставляют в уравнения равновесия. В результате получаем систему линейных алгебраических уравнений относительно значений напряжений 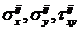 .
.
Рассмотрим пример, приведенный на рис. 7.3.
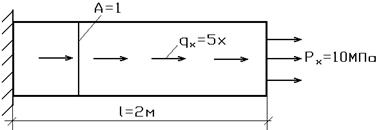
Рис.7.3
Рассмотрим задачу отыскания 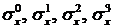 в точках с координатами:
в точках с координатами:
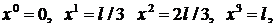
Эти величины найдем из условий равновесия:
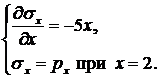
Для граничного элемента получаем 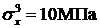 .
.
Для внутренних элементов:
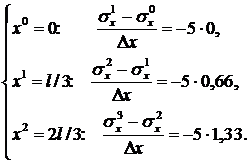
Получилось 3 уравнения с 3-я неизвестными. Учитывая, что 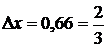 , получим:
, получим:
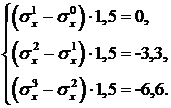
Из третьего уравнения с учетом того, что 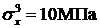 , найдем:
, найдем:
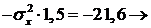
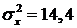
Из второго и первого уравнений вытекает, что
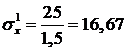 ,
, 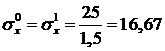 .
.
К недостатку метода можно отнести то, что в случае плоской задачи, если область не прямоугольная, трудно записываются уравнения равновесия граничных элементов.
Достоинства метода заключаются в следующем.
1) Сразу получаем значения искомых функций
2) Легко следить за сходимостью метода при увеличении числа неизвестных.
Метод конечных элементов
МКЭ вобрал в себя положительные стороны и МКР, и метода Рэлея-Ритца. МКЭ основан на законе сохранения энергии, записанного в форме принципа виртуальных перемещений. Суть МКЭ заключатся в следующем.
1. Тело представляют в виде набора элементов с объемами 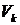 :
:
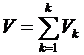 .
.
2. В каждом элементе 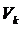 аппроксимируют искомые перемещения:
аппроксимируют искомые перемещения:
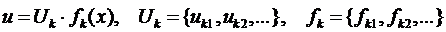 ,
,
здесь 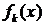 – выбираемые расчетчиком вектор известных функций,
– выбираемые расчетчиком вектор известных функций, 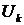 - вектор искомых узловых перемещений.
- вектор искомых узловых перемещений.
Наборы функций 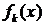 на сегодня имеются в большом количестве.
на сегодня имеются в большом количестве.
3. На каждом элементе вычисляется работа внешних сил и накопленная упругая энергия элемента.
4. Все это подставляется в закон сохранения, например, в принцип возможных перемещений. В качестве 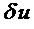 берутся какие-либо возможные перемещения. Обычно в качестве них берут соотношения
берутся какие-либо возможные перемещения. Обычно в качестве них берут соотношения 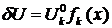 , но с заданными значениями узловых перемещений
, но с заданными значениями узловых перемещений 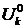 . При этом для получения систем уравнений применяют следующую процедуру. Сначала принимают
. При этом для получения систем уравнений применяют следующую процедуру. Сначала принимают 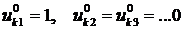 , далее берут
, далее берут 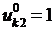 все остальные равны нулю и т.д.
все остальные равны нулю и т.д.
В результате получим столько уравнений, сколько неизвестных.
Рассмотрим пример расчета бруса, приведенного на рис.8.1.
Пусть известно, что Р0=25 МПа; q=x2 МПа; l=3м. Найти перемещения узлов1,2 (т.е. u1, u2).
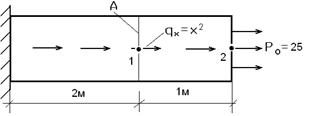
Рис.8.1
Разобьем стержень на два элемента – первый длиной 2 м, второй длиной 1 м. На каждом из них аппроксимируем перемещения линейными зависимостями.
Рассмотрим первый элемент и аппроксимируем перемещение следующей линейной функцией:
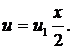
Тогда:
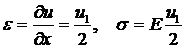 .
.
Рассмотрим второй элемент:
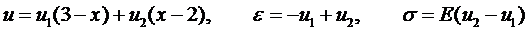 .
.
Подставим в закон сохранения (учитываем, что на правом торце 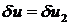 ):
):
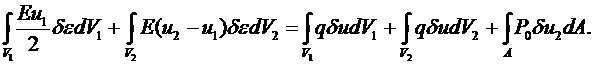
В качестве вариаций перемещений и деформаций (вооброжаемых перемещений и деформаций) примем:
1-й элемент: 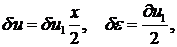
2-й элемент: 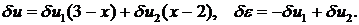
Полагая сначала 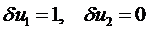 , получим первое уравнение:
, получим первое уравнение:
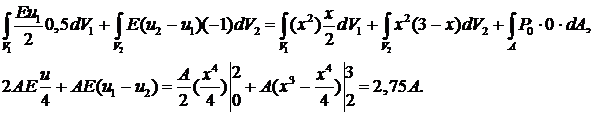
Полагая 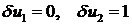 , получим второе уравнение:
, получим второе уравнение:
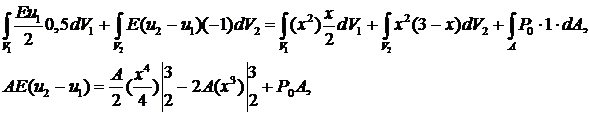
Таким образом, нашли систему уравнений относительно 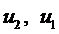 .
.
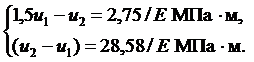
Выразим перемещение 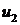 из второго уравнения:
из второго уравнения:
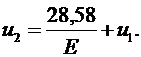
Из первого уравнения тогда находим:
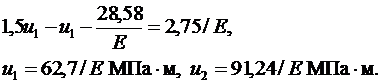
Теперь можно вычислить напряжения:
1 элемент: 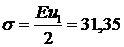 МПа, 2 элемент:
МПа, 2 элемент: 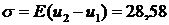 МПа.
МПа.
Достоинства метода
1. Решение сразу дает значения перемещений узлов упругого тела.
2. Легко проверяется сходимость метода при сгущении сетки.
3. Матрица системы уравнений получается симметрической и ленточной. Это позволяет экономить память ЭВМ и ускорять процесс решения.
4. В этом методе необходимо выполнять только геометрические граничные условия, например, задавать равными нулю перемещения закрепленных узлов. А записывать уравнение равновесия граничных и внутренних элементов как в методе Бубнова не нужно, поскольку закон сохранения энергии полностью эквивалентен этим уравнениям равновесия.
Недостатки метода
Распределение напряжений получается негладким. Для получения гладкого распределения напряжения существуют разные подходы. Наиболее часто применяемым является простейший метод осреднения напряжений в узлах (но он является наименее точным).
Приведем метод конечных элементов в матричной форме. Сначала проводится разбивка на элементы. Задача заключается в нумерации элементов, узлов и записи их связей.
Запись осуществляется в виде матрицы топологии, например, в виде:
[М] = [элементы, номера узлов]
М = 
Далее вводится аппроксимация перемещений на элементе.
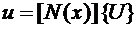 .
.
N – матрица, которая зависит от координат, {U} – вектор, составленный из перемещений узлов элемента, он является искомым.
Формы матрицы N на сегодня разработаны и имеются во всех пакетах МКЭ.
Например, в рассмотренной выше задаче N имеет вид:
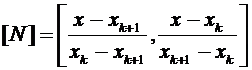 ,
,
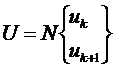 .
.
Далее вычисляются деформации по соотношениям Коши:
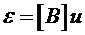 .
.
Тогда получим:
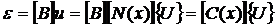 .
.
Затем записываем соотношения для напряжения по закону Гука.
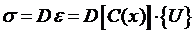 .
.
Выберем вариацию.
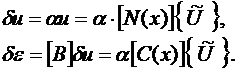
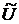 - воображаемый вектор узловых перемещений. Произвольность
- воображаемый вектор узловых перемещений. Произвольность 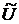 требуется согласно принципу Лагранжа.
требуется согласно принципу Лагранжа.
Подставим в принцип Лагранжа.
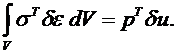
Здесь индексом Т обозначена операция транспонирования
Подставляя в принцип Лагранжа, получим:
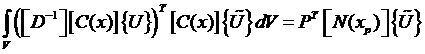 ,
,
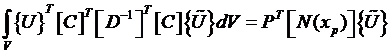 .
.
При интегрировании x, y, z исчезают. В результате получаем:
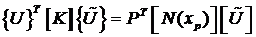 .
.
Здесь
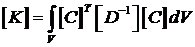 .
.
Матрица К называется матрицей жесткости.
Поскольку 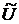 - произвольный вектор, то можно сначала положить
- произвольный вектор, то можно сначала положить
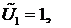
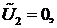
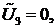 …
…
Тогда получим одно уравнение. Далее полагаем, что
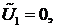
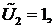
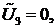 …
…
и получаем 2-е уравнение и т.д.
В результате получаем столько уравнений, сколько неизвестных. Эту систему можно записать в следующем виде:
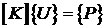 .
.
Решив эту систему уравнений, найдем перемещения каждого узла. После этого можно найти деформации и напряжения в элементах по соотношениям:
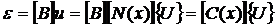 ,
,
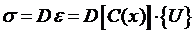 .
.
Задача Фламана
Рассмотрим задачу воздействия погонной силы Р на полубесконечное упругое тело.
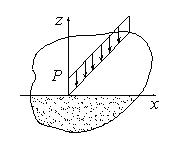
Рис.10.1
Это, например, расчетная схема давления на грунт ленточного фундамента.
Решение для этой задачи имеет вид:
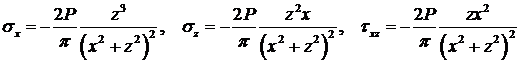 .
.
Проверяя уравнения равновесия (за исключением линии действия силы Р) для плоской задачи при qх = qz = 0, удостоверяемся, что оно удовлетворяется везде. Отметим также тот известный факт, что в линейной теории упругости решение единственно.
Проведем анализ решения.
При приближении к точкам приложения погонной силы P, (т.е. при 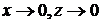 ) получаем, что
) получаем, что 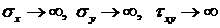 .
.
Это означает, что вблизи точек приложения погонной силы P использовать решение для расчета на прочность бессмысленно. Однако как выяснится ниже, эти решения подобного типа можно использовать для определения поля напряжений при воздействии нагрузки, распределенной по площади.
Исследуем вопрос о том, как можно применить решение задачи Фламана в задаче о действии внешнего давления в плоской задаче. Для этого рассмотрим действие давления q(x) на полупространство (рис.10.2). То, что q не зависит от у означает, что оно не меняется в направлении Оу.
Найдем 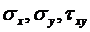 . Возьмем площадку dξ на расстоянии ξ от начала координати перейдем от распределенной нагрузки к сосредоточенной силе dP= q dξ. Получаем задачу Фламана. Как известно, при переносе начала координат влево на расстояние ξ любая функция f записывается в виде:
. Возьмем площадку dξ на расстоянии ξ от начала координати перейдем от распределенной нагрузки к сосредоточенной силе dP= q dξ. Получаем задачу Фламана. Как известно, при переносе начала координат влево на расстояние ξ любая функция f записывается в виде:
f(х - ξ).
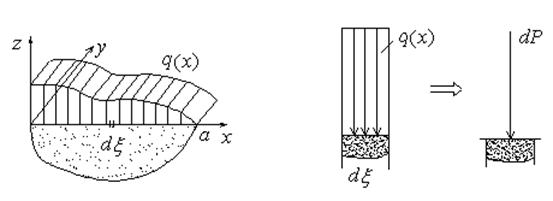
Рис.10.2 Рис.10.3
Тогда для силы dP решение можно записать в виде:
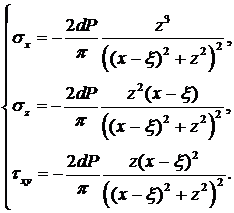
Такие же решения получим для других отрезков dξ, расположенных в других местах. Общее воздействие получим, суммируя напряжения от воздействия различных dP:
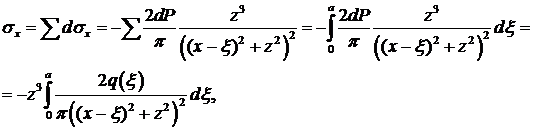
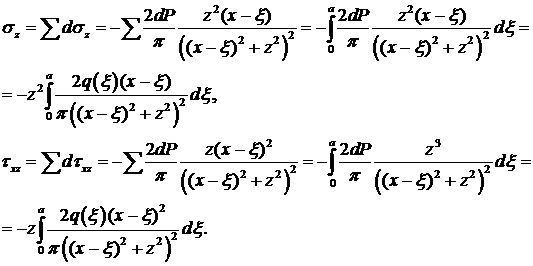 Пример. Пусть q = const = qo, а = 1. Тогда интегрируя, получим
Пример. Пусть q = const = qo, а = 1. Тогда интегрируя, получим
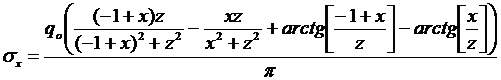 .
.
Аналогично можно найти 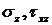 .
.
В этом случае бесконечных напряжений под нагрузкой не возникает (например, посередине при х=0.5 получим σх = 0.8183 q0). Поэтому при расчете ленточных фундаментов вместо сосредоточенной силы необходимо задавать нагрузку q(х), близкую к реальному распределенному давлению на основание.
Задача о трубе
Самую большую трудность в теории упругости всегда составляет удовлетворение уравнений равновесия элементов на границе и условий закрепления, но для ряда задач удается получить точное решение.
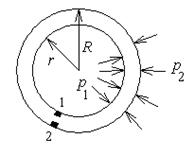
Рис.11.4
В этой задаче решение имеет вид:
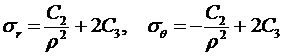 .
.
Сi – константы интегрирования уравнения. Их находят из условий равновесия граничных элементов 1 и 2. Выражения для них имеют вид:
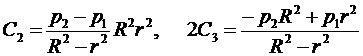 .
.
Здесь r и R - внутренний и внешний радиусы трубы. Рассмотрим, например, случай отсутствия внутреннего давления. Тогда
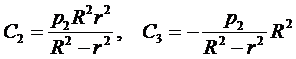 .
.
Так как R > r, то C3<0, а также ½С2/p½<½C3½, то видно, что sr уменьшается к центру, s 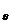 , наоборот, увеличивается к центру. Эпюры напряжений приведены на рис. 11.5. Чтобы проверить на прочность надо проанализировать условие:
, наоборот, увеличивается к центру. Эпюры напряжений приведены на рис. 11.5. Чтобы проверить на прочность надо проанализировать условие:
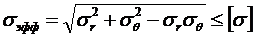 .
.
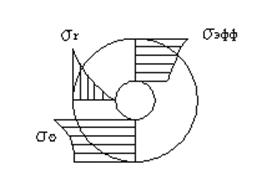
Рис.11.5
Форма кривой sэфф сильно зависит от отношения 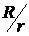 .
.
Задача Кирша
Это задача о растяжении бесконечной пластины с круглым отверстием.
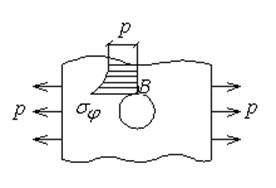
Рис.12.1
Оказывается, что система уравнений в полярной системе координат позволяет решить и кососимметричные задачи. Одной из них является задача о растяжении пластины с отверстием (пластина считается бесконечной). Задача Кирша знаменита тем, что позволяет найти (sj)max. Оказывается, что (sj)max = 3р. Независимо от размеров и от упругих характеристик материала оно возникает в точке В.
Задачи подобного типа для разных видов отверстий называются задачами о концентрации напряжений.
Следствие: при расчете даже простых тел (типа стержней при растяжении), но с круговыми отверстиями (даже для малого размера отверстия) мы должны увеличивать в 3 раза напряжение, вычисляемое по формуле 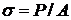 .
.
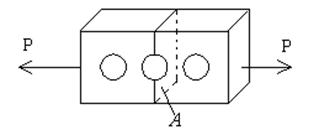
Рис.12.2
Задачи термоупругости
Запишем закон Дюгамеля-Неймана (закон линейного температурного расширения), который гласит, что при изменении температуры тела на величину 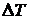 оно изменяет свои линейные размеры. Температурная линейная деформация при этом прямо пропорциональна перепаду температуры:
оно изменяет свои линейные размеры. Температурная линейная деформация при этом прямо пропорциональна перепаду температуры:
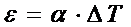 .
.
Тогда обобщенный закон Гука с учетом закона Дюгамеля- Неймана примет вид:
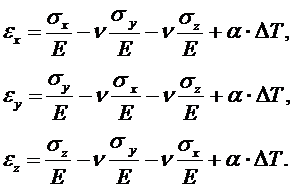
Для изотропного тела изменение температуры не приводит к сдвигам, поэтому:
