Алгоритм приведения формулы к КНФ

1. Исходная формула приводится к регулярному виду

2. Раскрываются скобки с применением 2-го дистрибутивного закона ( 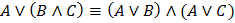) (сложение – конъюнкция, умножение – дизъюнкция)

Применение нормальных форм

I. Распознавание тождественной истинности формул

Формула тождественно истинна тогда и только тогда, когда каждая элементарная дизъюнкция ее КНФ содержат хотя бы одну высказывательную переменную вместе со своим отрицанием.

Алгоритм проверки формулы на тождественную истинность

1. Привести формулу к КНФ

2. Проверить, каждая ли элементарная дизъюнкция содержат высказывательную переменную вместе с ее отрицанием;

3. Если такая пара содержится в каждой элементарной дизъюнкции, то формула тождественно истинна; если такой пары нет хотя бы в одной элементарной дизъюнкции, то формула не тождественно истинна

II. Составление формулы по заданной таблице истинности.

В таблице истинности выбираем строки, где значение функции равно 0 и выписываем дизъюнкции всех переменных, причем, если переменная в этом наборе = 0, то записываем ее саму, а если переменная = 1, то ее отрицание. Конъюнкция этих дизъюнкций и будет искомой формулой.

Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой:

1) различны все члены конъюнкции;

2) различны все члены каждой дизъюнкции;

3) ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной;

4) каждая дизъюнкция содержит все переменные, входящие в исходную формулу

Способы приведения к совершенным нормальным формам

1-й способ – аналитический.

Алгоритм приведения к СКНФ аналитическим способом

1) привести формулу с помощью равносильных преобразований к КНФ;

2) удалить члены конъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);

3) из одинаковых членов конъюнкции (если такие окажутся) удалить все, кроме одного;

4) из одинаковых членов каждой дизъюнкции (если такие окажутся) удалить все, кроме одного;

5) если в какой-нибудь дизъюнкции не содержится переменной x_i из числа переменных, входящих в исходную формулу, добавить к этой дизъюнкции член и применить закон дистрибутивности дизъюнкции относительно конъюнкции;

6) если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.

7) Полученная формула и является СКНФ данной формулы.

2-й способ – табличный.

Алгоритм приведения к СКНФ табличным способом

Рассматриваем только те строки таблицы, где формула принимает значение 0. Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Причем аргумент, принимающий значение 0, берется без отрицания, значение 1 – с отрицанием. Наконец, образуют конъюнкцию полученных дизъюнкций.

Входной контроль

1. Запишите определения понятий «КНФ», «СКНФ».

2. Какие способы приведения формулы к СКНФ вы знаете?

3. Составьте и заполните сравнительную таблицу СКНФ и СДНФ:

№ п/п	Критерий сравнения	СКНФ	СДНФ
1.	Используемые логические операции	Конъюнкция, дизъюнкция	Конъюнкция, дизъюнкция
2.	…
3.
4.
5.

Ход работы

Задание 1. Привести формулу к СКНФ с помощью равносильных преобразований:

Решение:

Приводим формулу с помощью равносильных преобразований к КНФ:

Членов конъюнкции, содержащих переменную вместе с ее отрицанием, в полученной КНФ нет. Одинаковых членов конъюнкции нет. Одинаковых членов каждой дизъюнкции нет.

В первой дизъюнкции содержатся все переменные, входящие в исходную формулу.

Во второй дизъюнкции не содержится переменная Y, поэтому к этой дизъюнкции добавляем член и применяем закон дистрибутивности дизъюнкции относительно конъюнкции.

В третьей дизъюнкции не содержится переменная X, поэтому к этой дизъюнкции добавляем член и применяем закон дистрибутивности дизъюнкции относительно конъюнкции.

Удаляем одинаковые члены конъюнкции, оставляя только один, и . Получаем, что СКНФ имеет вид:

Задание 2.

По построенной в предыдущем практическом занятии таблице истинности (см. задание №2 в Ходе работы), найти СКНФ, найти минимальную КНФ для высказывания:

Решение.

Таблица истинности высказывания: :

x	y	z
1	1	1	0	1	0	0
1	0	1	1	0	1	1
1	1	0	0	1	1	1
1	0	0	1	0	0	1
0	1	1	0	1	0	0
0	0	1	1	1	1	1
0	1	0	0	1	1	1
0	0	0	1	1	0	0

По таблице составляем конъюнктивную нормальную форму (КНФ). Выбираем в таблице строки, в которых булева функция принимает значение 0. В данном случае – это 1-ая, 5-ая, и 8-ая строки.

Для каждой строки составляем дизъюнкцию: если значение переменной равно 1, то берем ее отрицание, а если 0, то берем саму переменную. Затем составляем конъюнкцию полученных дизъюнкций:

Эта формула и есть СКНФ.

Минимальную КНФ найдем по карте Карно по алгоритму:

1) Составляем таблицу Карно для булевой функции.

2) Разбиваем таблицу на прямоугольные контура, состоящие из 0 площадью 2^n-i, где n – число переменных, i = 0,1,2, …, n.

Количество контуров должно быть минимально, а площадь каждого как можно больше.

При этом следует учитывать:

- одни и те же клетки могут входить в несколько контуров;

- при проведении контуров крайние строки таблицы и ее крайние столбцы считаются соседними (так называемое правило цилиндра).

3) Далее записывается результирующая КНФ, т.е. конъюнкция элементарных дизъюнкций переменных, не меняющихся в пределах одного контура.

XY Z	00

I:

II:

МКНФ:

Выходной контроль

(выполните самостоятельно по вариантам)

Задание 1.

Привести формулу к СКНФ с помощью равносильных преобразований

Вариант 1 Вариант 2

1. 1.

2. 2.

Задание 2.

Построить таблицу истинности, найти СКНФ, найти минимальную КНФ для высказываний.

Вариант 1 Вариант 2

1. 1.

2. 2.

3. 3.

Контрольные вопросы

На выполнение тестового контроля отводится 12 минут. Работа состоит из 5 заданий.

К каждому заданию с выбором ответа даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.

Тест выбора

Задание №1.

Вопрос:Конъюнктивной нормальной формой логических функций называется…

Варианты ответов:

а) Дизъюнкция элементарных конъюнкций

б) Конъюнкция элементарных дизъюнкций

в) Дизъюнкция импликаций

г) Конъюнкция импликаций

Задание №2.

Вопрос: Булева функция обращается в нуль только на наборах: (0;0;0), (0;1;0), (1;1;0). Тогда СКНФ:

Варианты ответа:

а) ;

б) ;

в) ;

г) .

Задание №3.

Вопрос:Для формулы СКНФ является:

Варианты ответов:

а) ; б) ;

в) ; г) .

Задание №4.

Вопрос:Выражение представлено в форме

Варианты ответа:

а) ДНФ

б) КНФ

в) СДНФ

г) СКНФ

Задание №5.

Вопрос:Выражение представлено в форме

Варианты ответа:

а) ДНФ

б) КНФ

в) СДНФ

г) СКНФ

Условия выполнения:

Задание выполняется письменно в отчете по практическому занятию.

Время на подготовку – 2 мин.

Время на выполнение – 10 мин.

Используются тестовые задания одного типа - тест выбора.

При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания записывается номер выбранного ответа.

Критерии оценки:

За каждый правильный ответ выставляется 1 балл.

За не правильный ответ на вопрос выставляется 0 баллов.

Максимальное количество баллов за правильные ответы - 5.

Шкала оценки образовательных достижений:

Кол-во правильных ответов	Процент результативности (правильных ответов)	Оценка уровня подготовки
балл (отметка)	вербальный аналог
	90 ÷ 100		отлично
	80 ÷ 89		хорошо
	70 ÷ 79		удовлетворительно
Менее 3	менее 70		неудовлетворительно

Список литературы

Основные источники:

1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.

2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.

Дополнительные источники:

1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.

2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.

3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.

Практическое занятие № 7

Тема: Проверка булевой функции на принадлежность к классам Т₀, Т₁, S, L, M.

Цель: Научиться определять, к какому классу принадлежит булева функция.

Теоретические основы

Булева функция – это функция, и аргументы и значение которой принадлежит множеству {0, 1}.

Классы Поста

Т₀ - класс функций, сохраняющих нуль (т.е. если f(0,0,...,0)=0, то f принадлежит этому классу).

F(x,y)=x∨y принадлежит классу Т₀, так как 0∨0=0

F(x)= не принадлежит классу Т₀, так как

Т₁ - класс функций, сохраняющих единицу (т.е если f(1,1,...,1)=1, то f принадлежит этому классу).

F(x,y)=x∨y принадлежит классу Т₁, так как 1∨1=1

F(x)= не принадлежит классу Т₁, так как

L- класс функций, представимых линейным многочленом Жегалкина (т.е. в нем нет слагаемых, имеющих степень выше первой)

F(x,y)=x∨y=xy⊕x⊕y - нелинейный многочлен, значит, функция не принадлежит классу L.

F(x)= =x⊕1 - линейный многочлен, значит, функция принадлежит этому классу.

S- класс самодвойственных функций, т.е. таких функций, у которых столбец в таблице истинности ее значений переходит сам в себя при инвертировании. То есть, например, первое значение функции должно равняться отрицанию последнего, второе - отрицании предпоследнего, и так далее.

x	y	x∨y		x

Самодвойственной функцией является функция .

M-класс монотонных функций: если для любой пары наборов α и β таких, что α β, выполняется условие f(α)≤ f(β).

Уточнение: для сравнения наборов используется правило - набор α меньше набора β тогда и только тогда, когда каждый элемент α не больше соответствующего элемента β, и хотя бы один элемент α меньше соответствующего элемента β.

Например, набор (0, 1, 0) меньше набора (1, 1, 1).

А про наборы (1, 1, 0) и (1, 0, 1) нельзя сказать, что один меньше другого.

Для проверки функции на монотонность используют рисунок, называемый диаграммой Хассе.

Идея здесь состоит в том, чтобы сравнивать не каждый два набора из восьми, а меньшее количество пар. Возле каждого набора переменных пишем значение функции на этом наборе.

При этом, если будет нарушение монотонности, оно обнаружится на диаграмме.

Тогда, функция не монотонна, а функция x∨y - монотонна.

Входной контроль

1. Запишите определение булевой функции.

2. Какие существуют классы Поста?

3. Приведите примеры линейного и нелинейного полиномов Жегалкина, отличные от примеров, указанных в Теоретических основах.