Алгоритм приведения формулы к ДНФ
1. Исходная формула приводится к регулярному виду
2. Раскрываются скобки с применением 1-го дистрибутивного закона ( 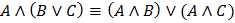 ) (сложение - дизъюнкция, умножение – конъюнкция)
) (сложение - дизъюнкция, умножение – конъюнкция)
Применение нормальных форм
I. Распознавание тождественной ложности формул
Формула тождественно ложна тогда и только тогда, когда каждая элементарная конъюнкция ее ДНФ содержат хотя бы одну высказывательную переменную вместе со своим отрицанием.
Алгоритм проверки формулы на тождественную ложность
1. Привести формулу к ДНФ
2. Проверить, каждая ли элементарная конъюнкция содержат высказывательную переменную вместе с ее отрицанием;
3. Если такая пара содержится в каждой элементарной конъюнкции, то формула тождественно ложна, т.е. невыполнима; если такой пары нет хотя бы в одной элементарной конъюнкции, то формула не является тождественно ложной.
II. Составление формулы по заданной таблице истинности.
В таблице истинности выбираем строки, где значение функции равно 1 и выписываем конъюнкции всех переменных, причем, если переменная в этом наборе равна 1, то записываем ее саму, а если переменная = 0, то ее отрицание. Дизъюнкция этих конъюнкций и будет искомой формулой.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой:
1) различны все члены дизъюнкции;
2) различны все члены каждой конъюнкции;
3) ни одна конъюнкция не содержит одновременно переменную и отрицание этой переменной;
4) каждая конъюнкция содержит все переменные, входящие в формулу
Способы приведения к совершенным нормальным формам
1-й способ – аналитический
Алгоритм приведения к СДНФ аналитическим способом
1) привести формулу с помощью равносильных преобразований к ДНФ;
2) удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);
3) из одинаковых членов дизъюнкции (если такие окажутся) удалить все, кроме одного;
4) из одинаковых членов каждой конъюнкции (если такие окажутся) удалить все, кроме одного;
5) если в какой-нибудь конъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член 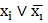 и применить закон дистрибутивности конъюнкции относительно дизъюнкции;
и применить закон дистрибутивности конъюнкции относительно дизъюнкции;
6) если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
7) Полученная формула и является СДНФ данной формулы.
2-й способ – табличный
Алгоритм приведения к СДНФ табличным способом:
Строим таблицу значений формулы. Рассматриваем только те строки, в которых значение формулы равно единице. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем, аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 – без отрицания. Наконец, образуем дизъюнкцию всех полученных конъюнкций.
Входной контроль
1. Запишите определения понятий «ДНФ», «СДНФ».
2. Для чего в математической логике применяются нормальные формы?
3. Какие способы приведения формулы к СДНФ вы знаете?
4. Составьте и заполните сравнительную таблицу ДНФ и СДНФ:
| № п/п | Критерий сравнения | ДНФ | СДНФ |
| 1. | Количество переменных в каждой конъюнкции | Может быть различным | Равно количеству переменных, используемых в формуле |
| 2. | … | ||
| 3. | |||
| 4. | |||
| 5. |
Ход работы
Задание 1. Привести формулу  к СДНФ с помощью равносильных преобразований:
к СДНФ с помощью равносильных преобразований:
Решение:
Приводим формулу с помощью равносильных преобразований к ДНФ:
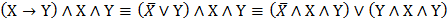
Удаляем члены дизъюнкции, содержащие переменную вместе с ее отрицанием, остается:
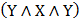
Из одинаковых членов каждой конъюнкции удаляем все, кроме одного, получаем:
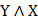
Полученная формула и является СДНФ данной формулы.
Задание 2.
Построить таблицу истинности, найти СДНФ, найти минимальную ДНФ для высказывания: 
Решение.
Строим таблицу истинности - таблицу, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний.
Сложением по модулю два (альтернативной дизъюнкцией, логи́ческим сложе́нием, исключа́ющим «ИЛИ», строгой дизъюнкцией) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда оба высказывания х и y принимают разные значения. Дизъюнкция обозначается х Å y (читается: «или х, или y»).
Таблица истинности для х Å y имеет вид:
| х | y | х Å y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Штрих Шеффера – это отрицание конъюнкции - обозначается x|y , задаётся следующей таблицей истинности:
| х | y | x|y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Таблица истинности высказывания:  :
:
| x | y | z |  |  |  |  |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
По таблице составляем дизъюнктивную нормальную форму (ДНФ). ДНФ в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции нескольких конъюнкций.
Выбираем в таблице строки, в которых булева функция принимает значение 1. В данном случае – это 2-ая, 3-ая, 4-ая, 6-ая и 7-ая строки.
Для каждой строки составляем конъюнкцию: если значение переменной равно 0. то берем ее отрицание, а если 1, то берем саму переменную. Затем составляем дизъюнкцию полученных конъюнкций:
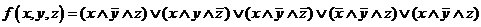 .
.
Эта формула и есть СДНФ.
Минимальную ДНФ найдем по карте Карно по алгоритму:
1) Составляем таблицу Карно для булевой функции.
2) Разбиваем таблицу на прямоугольные контура, состоящие из 1 площадью 2n-i, где n – число переменных, i = 0,1,2, …, n.
Количество контуров должно быть минимально, а площадь каждого как можно больше.
При этом следует учитывать:
- одни и те же клетки могут входить в несколько контуров;
- при проведении контуров крайние строки таблицы и ее крайние столбцы считаются соседними (так называемое правило цилиндра).
3) Далее записывается результирующая ДНФ, т.е. дизъюнкция элементарных конъюнкций переменных, не меняющихся в пределах одного контура.
| XY Z |  00 00 | |||
I: 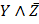
II: 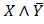
III: 
МДНФ: 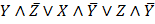
Выходной контроль
(выполните самостоятельно по вариантам)
Задание 1.
Привести формулу к СДНФ с помощью равносильных преобразований
Вариант 1 Вариант 2
1.  1.
1. 
2.  2.
2. 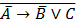
3.  3.
3. 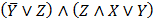
Задание 2.
Построить таблицу истинности, найти СДНФ, найти минимальную ДНФ для высказываний.
Вариант 1 Вариант 2
1.  1.
1. 

2. 
 2.
2. 
3.  3.
3. 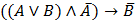
Контрольные вопросы
На выполнение тестового контроля отводится 12 минут. Работа состоит из 5 заданий.
К каждому заданию с выбором ответа даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.
Тест выбора
Задание №1.
Вопрос:Логическая функция трех переменных, представленная булевой функцией в виде СДНФ (умножение в формуле соответствует логической операции «конъюнкция»):
Варианты ответа:
а) 
б) 
в) 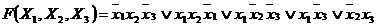
г) 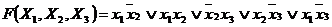
Задание №2.
Вопрос: Булева функция обращается в единицу только на наборах: (0;0;0), (1;0;0),. (1;0;1), (0;0;1) Тогда СДНФ имеет вид:
Варианты ответа:
а)  ;
;
б)  ;
;
в) 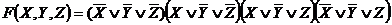 ;
;
г) 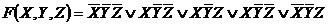 .
.
Задание №3.
Вопрос:Дизъюнктивной нормальной формой логических функций называется…
Варианты ответов:
а) Дизъюнкция элементарных конъюнкций
б) Конъюнкция элементарных дизъюнкций
в) Дизъюнкция импликаций
г) Конъюнкция импликаций
Задание №4.
Вопрос:Выражение 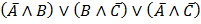 представлено в форме
представлено в форме
Варианты ответа:
а) ДНФ
б) КНФ
в) СДНФ
г) СКНФ
Задание №5.
Вопрос:Выражение 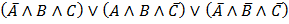 представлено в форме
представлено в форме
Варианты ответа:
а) ДНФ
б) КНФ
в) СДНФ
г) СКНФ
Условия выполнения:
Задание выполняется письменно в отчете по практическому занятию.
Время на подготовку – 2 мин.
Время на выполнение – 10 мин.
Используются тестовые задания одного типа - тест выбора.
При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания записывается номер выбранного ответа.
Критерии оценки:
За каждый правильный ответ выставляется 1 балл.
За не правильный ответ на вопрос выставляется 0 баллов.
Максимальное количество баллов за правильные ответы - 5.
Шкала оценки образовательных достижений:
| Кол-во правильных ответов | Процент результативности (правильных ответов) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | ||
| 90 ÷ 100 | отлично | ||
| 80 ÷ 89 | хорошо | ||
| 70 ÷ 79 | удовлетворительно | ||
| Менее 3 | менее 70 | неудовлетворительно |
Список литературы
Основные источники:
1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.
2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.
Дополнительные источники:
1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.
2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.
3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.
Практическое занятие № 6
Тема: Представление булевой функции в виде совершенной КНФ.
Цель: Научиться представлять булевой функции в виде совершенной КНФ.
Теоретические основы
Булевы функции названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой нетривиальный класс дискретных функций - их аргументы и значения могут принимать всего два значения.
Булевы функции находят применение в математической логике, электротехнике, многих разделах информатики.
В математической логике каждую переменную можно рассматривать как некоторое элементарное высказывание, принимающее одно из двух значений: 1 (истина) или 0 (ложь). Сложным высказываниям соответствуют формулы, построенные из элементарных высказываний с помощью логических связок. Вычисляя значения задаваемых ими функций, можно устанавливать зависимости истинностных значений сложных высказываний от значений входящих в них элементарных высказываний.
Формулу называют элементарной конъюнкцией (дизъюнкцией), если она является конъюнкцией (дизъюнкцией) одной или нескольких переменных, взятых с отрицанием или без отрицания.
Одну переменную или ее отрицание считают одночленной элементарной конъюнкцией (или элементарной дизъюнкцией).
Пример.Элементарные конъюнкции -  ; первые две из них — одночленными; элементарные дизъюнкции -
; первые две из них — одночленными; элементарные дизъюнкции - 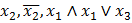 .
.
Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
КНФ записываются в виде 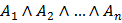 , где каждое Ai - элементарная дизъюнкция.
, где каждое Ai - элементарная дизъюнкция.
Пример.  - конъюнктивные нормальные формы.
- конъюнктивные нормальные формы.
Определение.
Формула называется регулярной, если в этой формуле нет импликаций, а отрицания, если они есть, относятся только к элементарным формулам.
