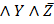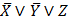Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
1. Отрицание
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквиваленция
Алгоритм построения таблицы истинности
1) Определить число строк (оно вычисляется по формуле k =2n, где k – количество строк, а n – число различных пропозициональных переменных, входящих в формулу).
2) Задать все комбинации совместной истинности/ложности переменных.
3) Вычислить (построчно) значение каждой подформулы и формулы в целом, используя истинностные значения логических операций.
Входной контроль
1. Запишите определение сложного высказывания
2. Приведите 2 примера сложных высказываний из литературных произведений, кинофильмов.
3. Какие высказывания называются тавтологией?
Инструктаж по технике безопасности
Ход работы
1. Составить таблицу истинности сложного логического выражения:
а) 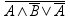
б) 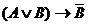
в) 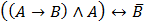
г) 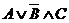
д) 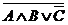
е) 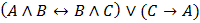
2. Найти значение логических выражений:
а) 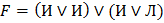
б) 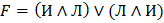
в) 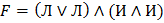
3. Проверить равносильность (эквивалентность) двух высказываний:
а) X=(A V B Λ C) и Y=((А V В) Λ (А V С))
б) 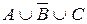 и
и 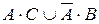
4. Установить, являются ли высказывания тавтологиями:
а) 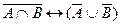
б) 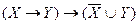
в) 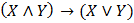
5. С помощью таблиц истинности установите, какое логическое выражение равносильно выражению 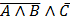
а) 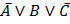
б) 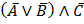
в) 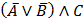
г) 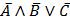
6. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| Л | И | Л | И |
| И | Л | И | Л |
| И | И | Л | Л |
Какое выражение соответствует F?
1) 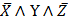
2) X ∨ 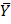 ∨ Z
∨ Z
3) X 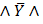 Z
Z
4) 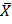 ∨ Y ∨ Z
∨ Y ∨ Z
Ответ подтвердите построением таблицы истинности. Дополните данную таблицу истинности.
Выходной контроль
(выполнить самостоятельно по вариантам)
1. Составить таблицу истинности сложного логического выражения:
| 1 вариант | 2 вариант | ||||||||||||||||||||||||||||||||
а) 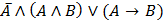 | а) 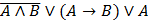 | ||||||||||||||||||||||||||||||||
б) 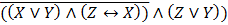 | б) 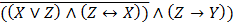 | ||||||||||||||||||||||||||||||||
| 2. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F? 1) (X ∨ 2) (X 3) (X ∨ 4) X Ответ подтвердите построением таблицы истинности. Дополните данную таблицу истинности. | 2. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F? 1) 2) X 3) X ∨ 4) Ответ подтвердите построением таблицы истинности. Дополните данную таблицу истинности. |
Контрольные вопросы
На выполнение тестового контроля отводится 12 минут. Работа состоит из 5 заданий.
К каждому заданию с выбором ответа даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.
Тест выбора
Задание №1.Значения, которые может принимать высказывание
Вопрос:
Варианты ответа:
а) дизъюнкция - конъюнкция;
б) импликация - эквиваленция;
в) истина - ложь;
г) равенство - неравенство.
Задание №2.
Вопрос: Таблица истинности - это таблица, которая ...
Варианты ответа:
а)  определяет только истинные логические выражения, при всех возможных вариантах исходных данных
определяет только истинные логические выражения, при всех возможных вариантах исходных данных
б) определяет только ложные логические выражения, при всех возможных вариантах исходных данных
в)  определяет истинность или ложность логических выражений, при всех возможных вариантах исходных данных
определяет истинность или ложность логических выражений, при всех возможных вариантах исходных данных
г)  определяет истинность или ложность логических выражений, только при ложных вариантах исходных данных
определяет истинность или ложность логических выражений, только при ложных вариантах исходных данных
Задание №3.
Вопрос:Высказывания бывают ...
Варианты ответов:
а) правильными – неправильным;
б) короткими - длинными;
в) известными - неизвестными;
г) простыми - составными (сложными).
Задание №4.
Вопрос:Количество строк в таблице истинности должно быть равно ... ( ^ - знак степени)
Варианты ответа:
а) = 2 ^ N ( где N - это количество переменных )
б) = 2 ^ N ( где N - это количество логических операций)
в) = 2 ^ N + 1 ( где N - это количество переменных )
г) = 2 ^ N + 1( где N - это количество логических операций )
Задание №5.
Вопрос:Логические выражения называют равносильными, если ...
Варианты ответа:
а) в них одинаковое количество высказываний
б) в них одинаковое количество логических операций
в) в них одинаковое количество скобок
г) в них последние столбцы таблиц совпадают
Условия выполнения:
Задание выполняется письменно в отчете по практическому занятию.
Время на подготовку – 2 мин.
Время на выполнение – 10 мин.
Используются тестовые задания одного типа - тест выбора.
При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания записывается номер выбранного ответа.
Критерии оценки:
За каждый правильный ответ выставляется 1 балл.
За не правильный ответ на вопрос выставляется 0 баллов.
Максимальное количество баллов за правильные ответы - 5.
Шкала оценки образовательных достижений:
| Кол-во правильных ответов | Процент результативности (правильных ответов) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | ||
| 90 ÷ 100 | отлично | ||
| 80 ÷ 89 | хорошо | ||
| 70 ÷ 79 | удовлетворительно | ||
| Менее 3 | менее 70 | неудовлетворительно |
Список литературы
Основные источники:
1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.
2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.
Дополнительные источники:
1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.
2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.
3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.
Практическое занятие № 4
Тема: Упрощение формул логики с помощью равносильных преобразований
Цель: Научиться упрощать формулы логики с помощью равносильных преобразований
Теоретические основы
Для преобразования функций, упрощения формул, полученных при формализации условий логических задач, в алгебре логики производятся эквивалентные преобразования, опирающиеся на основные логические законы.
В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул.
Две формулы с одними и теми же высказывательными переменными называются равносильными (эквивалентными), если они принимают одинаковые истинностные значения в каждой строке таблицы истинности.
Законы логики
1. Закон коммутативности
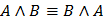
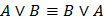
2. Закон ассоциативности
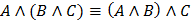
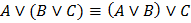
3. Закон дистрибутивности
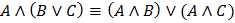
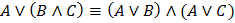
4. Закон двойного отрицания
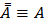
5. Законы де Моргана
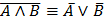
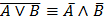
6. Закон отрицания импликации
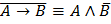
7. Закон устранения импликации
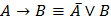
8. Закон контрапозиции
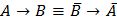
9. Закон противоречия
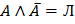
10. Закон исключенного третьего
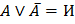
11. Законы исключения констант
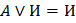
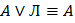
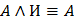
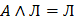
12. Законы поглощения
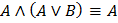
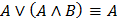
13. Идемпотентные законы:
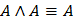
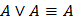
Входной контроль
1. Для чего применяются законы логики?
2. Какие две формулы называются эквивалентными?

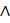 Z
Z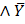 ) ∨ Z
) ∨ Z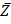
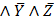
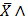
 Z
Z