Энергия колебаний и теплоемкость кристаллической решетки

Энергию колебаний и теплоемкость решетки будем рассчитывать для единичного объема кристалла, т. е. положим нормировочный объем равным единице: V = L³ = 1.

Чтобы вычислить среднюю энергию колебаний кристаллической решетки, нужно просуммировать среднюю энергию всех типов колебаний (всех состояний фононов):

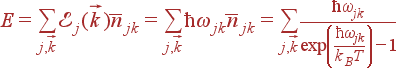(44)

Проще всего это сделать при высоких температурах, когда для частот всех колебаний выполняется неравенство ħω_jk<< k_BT (классический предел). Тогда средняя энергия, приходящаяся на каждое колебание, равна k_BT, всего колебаний 3lN = 3lN, для полной энергии E получаем:

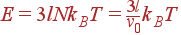(45)

Т. к. N — число примитивных ячеек кристалла в единице объема, то N = 1/v₀, где v₀ — объем примитивной ячейки.

Теплоемкость решетки при высоких температурах постоянна (закон Дюлонга и Пти):

CV = 3lNkB

(46)

При невысоких температурах все сложнее. Чтобы точно вычислить энергию решетки, т. е. сосчитать сумму (44), необходимо знать дисперсионные зависимости для всех ветвей колебаний. И даже при условии, что зависимости эти известны, аналитическое выражение для энергии получить практически невозможно.

Поэтому для нахождения энергии и теплоемкости решетки применяют различные приближения.

Модель Эйнштейна

В модели Эйнштейна предполагается, что частоты всех фононов одинаковы, ω_jk = ω₁. Тогда для энергии получаем:

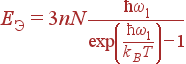(47)

При высоких температурах, k_BT>>ħω₁, эта зависимость приводит к выражению (45) для энергии и закону Дюлонга и Пти (46) для теплоемкости.

При низких температурах, k_BT<<ħω₁, энергия колебаний и теплоемкость экспоненциально уменьшаются:

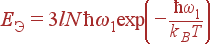(48)

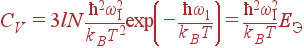(49)

Модель Эйнштейна хорошо описывает вклад в энергию и теплоемкость оптических ветвей фононов, у которых частота слабо зависит от волнового вектора и ее можно считать постоянной. Чтобы учесть только оптические ветви, частоту которых мы полагаем равной ω₁, нужно вместо 3l писать число этих ветвей. В общем случае, частоты разных оптических ветвей могут сильно отличаться друг от друга и их вклад в энергию и теплоемкость нужно учитывать отдельно.

Модель Дебая

Опыт показывает, что теплоемкость действительно падает с уменьшением температуры, но не экспоненциально, а пропорционально T³. Дело в том, что при любых, сколь угодно низких температурах в кристалле найдутся колебания, энергия фонона которых меньше k_BT. Это — длинноволновые акустические колебания. Именно такие колебания, точнее те из них, частота которых меньше k_BT/ħ, вносят основной вклад в энергию при низких температурах. Колебания с б\'ольшими частотами (оптические и более коротковолновые акустические) ''заморожены'': фононов этих колебаний экспоненциально мало.

Сделаем простую оценку. Вклад в энергию вносят фононы, энергия которых меньше kT. Пусть скорость звука j-й акустической ветви равна s_j и не зависит от направления волнового вектора: ω = s_j|k|. Тогда вклад в энергию дают колебания с волновыми векторами, меньшими k_max = k_BT/(ħ s_j). Плотность разрешенных значений волновых векторов в k-пространстве кристалла равна V/(2π)³, поэтому внутри сферы радиуса k_max содержится

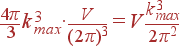разрешенных значений волновых векторов. Это число колебаний одной акустической ветви, вносящих существенный вклад в энергию. На каждое такое колебание приходится энергия порядка k_BT. Для энергии колебаний одной акустической ветви получаем:

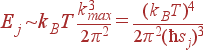(50)

Т. к. мы вычисляем энергию и теплоемкость единицы объема кристалла, то в (50) мы положили V = 1.

Таким образом, вклад одной акустической ветви в теплоемкость пропорционален T³:

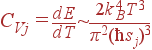(51)

Чтобы получить полную энергию и теплоемкость, надо сложить вклады от трех акустических ветвей:

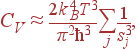(52)

где через s_j обозначена скорости звука j-й акустической ветви.

Мы сделали достаточно грубую оценку, поэтому к численным коэффициентам в последних двух выражениях не стоит относиться серьезно. Тем не менее, эта оценка дает правильную зависимость энергии и теплоемкости от температуры и скорости звука.

Посчитаем теперь энергию решетки при низких температурах более аккуратно.

Формула (44) имеет вид суммы по различным колебаниям (различным состояниям фононов) определенной величины, которая зависит только от энергии фонона:

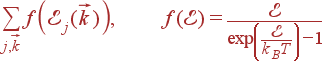(53)

Такие суммы встречаются довольно часто. Т. к. f зависит только от энергии фонона, то от суммы по состояниям можно перейти к интегралу по энергии:

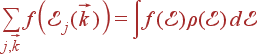(54)

Здесь 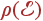— плотность состояний фононов. Напомним, что 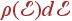— это число состояний квазичастиц (фононов) в единице объема с энергиями от 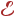до 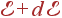, т. е. число различных колебаний с такими энергиями.

Суммарная плотность состояний складывается из плотности состояний разных ветвей: 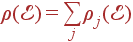; плотность состояний ветви определяется ее законом дисперсии 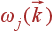. Аналитически получить законы дисперсии и плотности состояний фононов реальных кристаллов практически невозможно.

Однако при низких температурах энергия и теплоемкость определяются длинноволновыми акустическими фононами. Плотность состояний акустических фононов нам известна, мы получили ее в качестве примера, когда вводили само понятие плотности состояний (). Если для j-й акустической ветви ω = s_j|k|, то

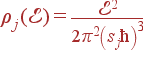(55)

Плотность состояний длинноволновых колебаний всех акустических ветвей получается суммированием по трем акустическим ветвям:

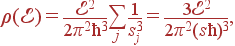(56)

где s — ''усредненная'' скорость звука:

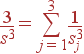(57)

Линейный закон дисперсии ω = s|k| и соответствующая плотность состояний верны только для малых k. При б\'ольших значениях волнового вектора закон дисперсии и плотность состояний имеют более сложный вид.

Однако при низких температурах вклад в энергию и теплоемкость вносят как раз только длинноволновые фононы, а при высоких температурах вид плотности состояний не важен, т. к. в этом случае на каждое колебание приходится энергия kT. Чтобы получить выражение, которое давало бы правильные предельные зависимости при низких и высоких температурах, Дебай предложил считать, что закон дисперсии ω = s|k| выполняется и при больших k. Максимальное значение волнового вектора k_D при этом выбирается так, чтобы в шаре радиуса k_D содержалось столько разрешенных значений волновых векторов, сколько их содержится в зоне Бриллюэна, N = 1/v₀. Иными словами, объем этого шара должен быть равен объему зоны Бриллюэна (2π)³/v₀, откуда

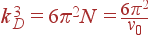(58)

Таким образом, сохраняя число акустических колебаний, мы заменяем первую зону Бриллюэна сферой, а реальный закон дисперсии — линейным. Фонон с волновым вектором k_D имеет энергию 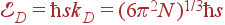. Соответствующая 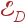температура,

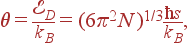(59)

называется температурой Дебая.

В таком приближении мы можем вычислить вклад акустических ветвей в энергию и теплоемкость решетки:

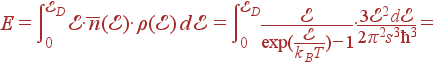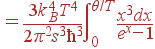(60)

При низких температурах, T<<θ, верхний предел интеграла много больше единицы. Благодаря экспоненте в знаменателе интеграл сходится очень быстро, что позволяет положить верхний предел равным бесконечности. Значение такого интеграла известно:

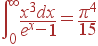(61)

Для энергии акустических колебаний при низких температурах получаем:

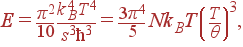(62)

откуда следует, что теплоемкость решетки при низких температурах пропорциональна T³:

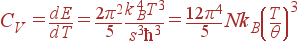(63)

При высоких температурах, T>>θ, верхний предел интегрирования мал, поэтому можно считать, что exp(x)–1≈ x, таким образом:

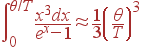(64)

E = 3NkT

(65)

CV = 3Nk

(66)

Это закон Дюлонга и Пти, только вместо полного числа колебаний 3lN стоит число колебаний акустических ветвей 3N. (При высоких температурах на каждое колебание приходится средняя энергия k_BT, полное число акустических колебаний равно 3N, поэтому вклад акустических ветвей в энергию равен 3NkT).

В пределе низких и высоких температур модель Дебая дает точные значения для вклада акустических ветвей в энергию и теплоемкость. В области же промежуточных температур, T~θ, эта модель лишь аппроксимирует реальную зависимость энергии и теплоемкости от температуры.

Температура Дебая разделяет две температурные области. В области низких температур на энергию и теплоемкость решетки сильное влияние оказывают квантовые эффекты (''вымерзание'' высокочастотных колебаний). В области высоких температур эти эффекты не существенны, и теплоемкость может быть вычислена в классическом приближении. Для большинства кристаллов температура Дебая лежит в интервале от 100 до 300K.

Чтобы получить полную энергию и теплоемкость кристаллической решетки, надо к вкладу акустических колебаний прибавить вклад оптических ветвей, для которого хорошим приближением является модель Эйнштейна. Этот вклад пренебрежимо мал при низких температурах. При высоких температурах вклады всех ветвей в энергию и теплоемкость равны.