Конспект урока ознакомления с новым материалом

Тема: «Умножение положительных и отрицательных чисел».

Цели: формирование знаний о правилах умножения положи тельных и отрицательных чисел и умений применять их ■ простейших случаях; развитие умений сравнивать, выяв лять закономерности, обобщать; воспитание ответственное го отношения к учебному труду.

Оборудование: модель термометра, плакат с изображением рисунка 89 из учебника, таблицы для устного счета.

Структура урока:

1. Постановка цели урока (2 мин).

2. Подготовка к изучению нового материала (3 мин).

3. Ознакомление с новым материалом (25 мин).

4. Первичное осмысление и применение изученного (10 мин).

5. Постановка домашнего задания (2 мин).

6. Подведение итогов урока (3 мин).

7. Резервные задания.

Ход урока

1. Постановка цели урока

Проверяется подготовленность классного помещения и го товность учащихся к уроку.

Отмечается, что изучение положительных и отрицательным чисел и действий над ними продолжается. Уточняется, что учя щиеся могут пока лишь складывать и вычитать положительные и отрицательные числа. Сегодня же будет рассматриваться во прос о том, как умножать положительные и отрицательные чис ла. Записывается тема урока: «Умножение положительных и от рицательных чисел».

2. Подготовка к изучению нового материала

В ходе фронтального опроса учащиеся приводят примеры положительных и отрицательных чисел, находят их модулей формулируют правила сложения и вычитания положительных и отрицательных чисел, приводят соответствующие им примеры,

Внимание учащихся акцентируется на нахождении моду ля данного числа и отыскании чисел с одинаковыми и разны­ми знаками, потому как эти сведения будут непосредственно ИМ пользованы при умножении положительных и отрицательных чисел. Достигается это решением заданий следующего вида:

а) назовите модуль каждого из чисел: -5; 12; -0,7;; 3,6;

б) выберите из предложенного выше набора чисел какие-
нибудь два числа с одинаковыми и два числа с разными
знаками.

3. Ознакомление с новым материалом

Прежде чем сформулировать правила умножения положи­тельных и отрицательных чисел, решаются задачи № 1104 и аналогичные им на изменение температуры. Условия последних четырех задач записываются на доске.

Задача 1. Температура воздуха повышается каждый день на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру воздуха будет показывать термометр через 3 дня?

Задача 2. Температура воздуха понижается каждый день на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру воздуха покажет термометр через 3 дня?

Задача 3. Температура воздуха повышалась каждый день на 2 °С. Сейчас термометр показывает 0 ^СС. Какую температуру воздуха показывал термометр 3 дня назад?

Задача 4. Температура воздуха понижается каждый день на 2 °С. Сейчас термометр показывает 0 °С. Какую температуру полдуха показывал термометр 3 дня назад?

С помощью плаката с изображением рисунка 89 из учеб­ника задачи 1104 (а, б) решает Иванов, а № 1104 (в, г) — Пе­трова. Решения записываются в следующем виде:

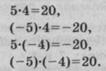
С использованием модели термометра Калинова решает задачи 1 и 2, а Нечаев — задачи 3 и 4. Записываются ихьрешения: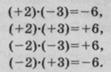

Обсудив вместе с остальными учащимися полученные ре­зультаты, сравнив их и выявив закономерности в определении знака произведения и его модуля, переходим к формулировке правил умножения двух чисел с разными знаками и двух отри­цательных чисел.

Подключаем зрительные анализаторы в процесс восприятии учащимися содержания введенных правил умножения че­рни их самостоятельное ознакомление с объяснительным текс­том п. 35 учебника.

Выделяем сведения из учебника, которые не рассматривались на уроке: задачи на расход ткани и зависимость, связанную с изменением знака произведения при изменении знака од­ного из множителей. Отвечая на вопросы учащихся, выясняем как умножать отрицательное число на нуль, и обращаем внимание на правила чтения произведений, в которые входят отрицательные числа.

Объяснение нового материала завершается обобщением изученного и формулировкой правил умножения чисел с разными и одинаковыми знаками. Они записываются учащимися в тетради.

Правило 1. Произведение двух чисел с разными знаками есть отрицательное число, модуль которого равен произведению модулей сомножителей.

Правило 2. Произведение двух чисел с одинаковыми знаками есть положительное число, модуль которого равен произведению модулей сомножителей.

Подобный подход к формулировке правил умножения положительных и отрицательных чисел не только дополняет учеб ник ранее изученным материалом, но и в большей степени способствует предупреждению типичных ошибок учащихся, связанных с потерей знака произведения. Мотивируется это тем, что в приводимых в учебнике правилах либо не говорится явно о знаке произведения, либо сначала говорится о модуле произведения, а затем о его знаке, что нарушает последовательность написания результата умножения чисел.

4. Первичное осмысление и применение изученного

Оно начинается с устных вычислений произведений с пояснениями при помощи следующих таблиц для устного счета представленных на рисунках 7 и 8.

Образец ответа в данном случае может быть таким: — Произведение минус трех и пяти равно минус пятнадцати, потому что при умножении двух чисел с разными знака

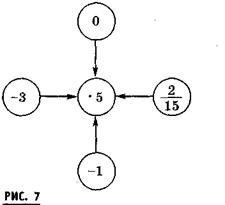
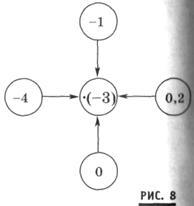
получается отрицательное число, а его модуль равен произведению модулей сомножителей, то есть трех и пяти. Далее опрашиваются Васильева, Михайлов, Степанов и Ильина. Они решают соответственно № 1102, 1103, 1105, 1106. При им добиваемся правильных и полных записей их решений учащимися. Например, образцы записей при решении № 1105 могут быть такими: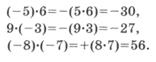

5. Постановка домашнего задания. На дом задается прочитать объяснительный текст п. 35 учбника, выучить наизусть правила 1 и 2, записанные в тетрадях, решить № 1127, ИЗО. Учащиеся предупреждаются, что на следующем уроке с помощью математического диктанта будут проверяться знание каждым учеником заданных правил, их внимание и умение применять в простейших случаях. Учащимся предоставляется возможность ознакомиться с содержанием домашнего задания и получить необходимые пояснения. 6. Подведение итогов урока Фронтальным опросом вместе с учащимися подводятся итога урока: — Какое действие с положительными и отрицательными числами мы рассматривали на уроке? — Как прочитать запись ?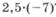

— Как перемножить два числа с разными знаками? — Привести пример на умножение двух чисел с разными знаками и решить его. — Как перемножить два числа с одинаковыми знаками? — Привести пример на умножение двух чисел с одинако­выми знаками и решить его. С учетом работы в течение всего урока комментируются и оцениваются ответы учащихся Иванова, Петровой, Калиновой, | Нечаева, Васильевой, Михайлова, Степанова и Ильиной.

7. Резервные задания

На случай досрочного выполнения всем классом рассмот­ренных выше заданий и обеспечения занятости и развития наиболее подготовленных учащихся планируется использовать также № 1120, 1122 и 1126.

***

В рассмотренном конспекте описание хода урока дано в произвольной форме. Другой подход к оформлению конспекта урока математики связан с выделением деятельности учителя и учащихся. Его специфику раскроем на примере оформления конспекта урока алгебры в VII классе по применению различными способов разложения многочлена на множители с использованием учебника Ш. А. Алимова, Ю. М. Колягина, Ю. В. Сидорова, Н. Е. Федоровой, М. И. Шабунина.

Урок-практикум

Тема: «Применение нескольких способов разложения многочле на на множители».

Цели: воспитывать волю и настойчивость для достижения конечных результатов при разложении многочленов на множители;

развивать навыки самоконтроля;

сформировать умения разлагать многочлен на множители вынесением общего множителя за скобки, группировкой применением формул сокращенного умножения.

Оборудование: кодоскоп, таблицы с формулами сокращения го умножения, раздаточный материал.

Структура урока:

1. Сообщение темы и цели практикума (2 мин).

2. Проверка домашнего задания (3 мин).

3. Актуализация опорных знаний и умений учащихся(5 мин).

4. Инструктирование по выполнению заданий практикуме (3 мин).

5. Выполнение заданий в группах (25 мин).

6. Проверка и обсуждение полученных результатов (5 мини

7. Постановка домашнего задания (2 мин).

8. Резервные задания.

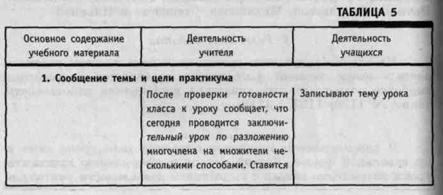
Ход урока (описан в табл. 5)

* * *

Рассмотрим, наконец, разновидность конспекта урока, отличающегося тем, что при его описании выделяется система вопросов и ответов на них, раскрывающих содержание урока. Специфику оформления такого конспекта покажем на примере раз- I работки урока геометрии в VIII классе по изучению свойств прямоугольника с использованием учебника А. В. Погорелова. 1

Комбинированный урок

Тема: «Прямоугольник».

Цели: развитие умений обобщать, абстрагировать и конкрети зировать свойства изучаемых объектов и отношений; формирование знаний о прямоугольнике и умений приме нять его определение и свойства на уровне обязательной подготовки; воспитание уважительного отношения к сверстникам.

Оборудование: переносные доски с готовыми чертежами, кар- I касные модели четырехугольников.

Структура урока:

1. Ознакомление с темой урока, постановка его целей
(2 мин).

2. Проверка домашнего задания (6 мин).

3. Систематизация знаний и умений по пройденному ма­териалу с использованием упражнений на готовых черте жах (8 мин).

4. Определение понятия прямоугольника и доказательство его свойств (12 мин).

5. Первичное закрепление изученного (12 мин).

6. Постановка домашнего задания (3 мин).

7. Подведение итогов урока (2 мин).

8. Резерв: дифференцированные задания.

Ход урока

1. Ознакомление с темой урока, постановка его целей

Вместе с дежурными учитель проверяет готовность класса; к уроку, после чего напоминает учащимся, что на этом заня­тии продолжается изучение темы «Четырехугольники». Сооб­щает, что сегодня будем рассматривать один из частных видов параллелограмма, его определение и свойства, начнем учиться их применять при решении задач.

2. Проверка домашнего задания

Семенова и Кустов вызываются для решения задач № 14, ] 20 § 6 из домашнего задания. Пока они оформляют решения | задач на доске, учитель заслушивает консультантов о выполнении остальными учащимися домашнего задания, отвечает на вопросы учащихся по домашнему заданию и осуществляет устную проверку знаний по изученному материалу о четырехугольни­ках постановкой вопросов типа:

— Какая фигура называется четырехугольником?

— Какие стороны четырехугольника называются противо­лежащими?

— Что такое параллелограмм?

— Каким свойством обладают противолежащие стороны па­раллелограмма?

Семенова и Кустов переходят к объяснению решений сво­их задач. Остальные учащиеся вместе с учителем контролиру­ют их ответы, оформление записей, корректируют и дополняют записи в своих тетрадях. По инициативе учителя учащиеся при­влекаются к постановке дополнительных вопросов отвечавшим.

Медведев. Ну вот ты знаешь, что такое диагонали четы­рехугольника?

Учитель добивается от Медведева уважительного обраще­ния к Семеновой.

Медведев. Скажи, пожалуйста, что такое диагонали четы­рехугольника.

Семенова. Отрезки, соединяющие противолежащие верши­ны четырехугольника, называются его диагоналями.

Учитель подтверждает правильность ее ответа, оценивает ее знания, затем знания Кустова и подводит итоги выполнения классом домашнего задания.

3. Систематизация знаний и умений по пройденному материалу

Для подготовки учащихся к усвоению нового материала повторяются и систематизируются их знания и умения в про­цессе устного решения упражнений на готовых чертежах. Вы­ставляется переносная доска с первой группой задач, оформлен­ных в виде таблицы 6.

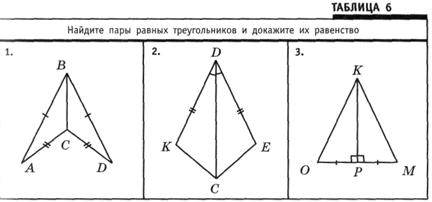
Учитель. Кто готов решить какую-нибудь из предложенных задач?

Осокина разъясняет решение первой задачи:

— У треугольников ABC и DBC AC=CD и AB=BD по условию, а ВС — общая сторона. Поэтому они равны по трем сторонам.

Ветрова решает вторую задачу:

— У треугольников DEC и DKC равны стороны DE и DK
и углы EDC и CDK, а сторона DC общая. Поэтому они равны
по двум сторонам и углу между ними.

А решение третьей задачи объясняет Борисов:

— У прямоугольных треугольников ОРК и МРК равны катеты ОР и РМ, а катет КР общий. Поэтому они равны по двум сторонам и углу между ними (или по двум катетам, если этот
признак равенства прямоугольных треугольников был сформулирован в процессе обучения).

Выставляется другая переносная доска с готовыми чертежами (см. табл. 7).

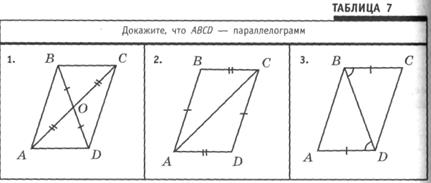
Учитель. Есть ли желающие решить какую-нибудь из этих трех задач?

Федоров решает первую задачу:

— У четырехугольника ABCD диагонали пересекаются в
точке О и делятся ею пополам, поэтому этот четырехугольник —
параллелограмм по теореме 6.1.

Девятова объясняет решение второй задачи:

— Треугольники ABC и ADC равны по трем сторонам, отсюда углы ВСА и CAD равны. Поэтому прямые ВС и AD параллельны по признаку параллельности прямых, а значит, параллельны и стороны ВС и AD. Аналогично параллельны стороны
АВ и CD. Тогда четырехугольник ABCD является параллелограммом по определению.

Решение третьей задачи поясняется Жигуновым:

— У четырехугольника ABCD противолежащие стороны ВС
и AD равны по условию и параллельны, так как прямые ВС и
AD параллельны по признаку параллельности прямых. Поэтому этот четырехугольник — параллелограмм по задаче 18 § 6.

Учитель подчеркивает, что повторенный материал будет использован также при изучении одного из известных им четы­рехугольников и записывает вместе с учащимися тему урока: * Прямоугольник ».

4. Определение понятия прямоугольника и доказательство его свойств

Для введения определения понятия прямоугольника рас­сматриваются следующие три каркасные модели четырехуголь­ников (см. рис. 9, 10, 11).

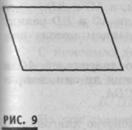
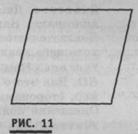
Учитель. Найдите по виду этих четырехугольников их общие свойства.

Ветрова. У каждого из них противолежащие стороны параллельны, поэтому все они являются параллелограммами. Учитель. А как еще называют средний из этих параллело­граммов?

Федоров. Прямоугольником.

Учитель. Чем отличается прямоугольник от двух других параллелограммов ? Осокина. У него все углы прямые.

Учитель диктует, а учащиеся записывают определение пря­моугольника:

«Прямоугольник — это параллелограмм, у которого все уг­лы прямые».

Учитель. Так как прямоугольник является параллелограм­мом, то он обладает всеми свойствами параллелограмма. Борисов, какими?

Борисов. У прямоугольника противолежащие стороны рав­ны и диагонали точкой пересечения делятся пополам. Учитель. Верно. Но прямоугольник имеет еще особое свой­ство, которое формулируется в виде теоремы 6.4: диагона­ли прямоугольника равны.

Для доказательства теоремы 6.4 на доске изображается пря­моугольник ABCD и его диагонали (рис. 12). Учитель повторяет формулировку теоремы и предлагает Девятовой продиктовать, что нам дано и что нужно дока­зать. Девятова затрудняется ответить.

Тогда учитель начинает пере водить формулировку теоремы из категоричной формы в условную: — Сформулируем теорему в другом виде, а именно:

если ABCD — прямоугольник, то Девятова, продолжи. Девятое а. ...Его диагонали равны Учитель. Девятова, а теперь мо жешь определить, что нам дано и 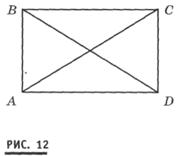что нужно доказать? Девятова. Да. ABCD — прямоугольник, а АС и BD диагонали. Надо доказать, что диагонали АС и BD равны Доказательство проводится с использованием метода восходящего анализа.

Учитель. Нам надо доказать равенство диагоналей АС и BD. Для этого сначала выясним, являются ли они, напри мер, сторонами треугольников BAD и CDА. Онищенко подтверждает этот факт.

Учитель. Для того, чтобы доказать равенство диагоналей достаточно доказать равенство, например, каких фигур? Лобова. Треугольников BAD и CDA.

Учитель. Для того чтобы доказать равенство треугольников BAD и CDA, что достаточно установить? Николаев. Что они прямоугольные, катет AD общий, а катеты АВ и CD равны как противолежащие стороны прямо угольника.

Учитель. Итак, треугольники BAD и CDA равны по двум катетам, а из их равенства следует и равенство гипотенуз Гипотенузы же есть диагонали прямоугольника. Теорема доказана.

Записи на доске при этом оформляются в следующем виде (см. табл. 8).

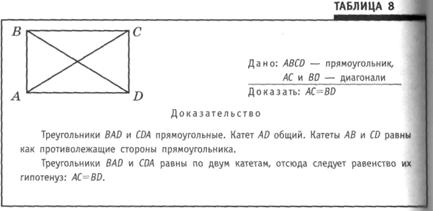
5. Первичное закрепление изученного

Для закрепления изученного учащимся предлагается сначала прочитать содержание п. 54 учебника. Затем учитель отвечает на возникшие у ребят вопросы и предлагает записать ре­зультат решенной в учебнике задачи № 24 в виде признака пря­моугольника:

— Если у параллелограмма все углы равны, то он является прямоугольником.

Далее решаются задачи № 25 и 26, для чего последова­тельно вызываются Николаев и Лобова. Результат решения заачи № 26 записывается в виде еще одного признака прямоугольника:

— Если у параллелограмма диагонали равны, то он являются прямоугольником.

С помощью дополнительных вопросов к отвечавшим уча­щимся повторяются и закрепляются изученные определение, свойства и признаки прямоугольника.

6. Постановка домашнего задания

На дом задается изучить содержание п. 54 и решить зада-I № 27, 28 § 6. Обращается внимание на то, что необходимо знать определение, свойства и признаки прямоугольника и уметь доказывать теорему 6.4.

Учащимся дается возможность ознакомиться с условиями дач № 27 и 28, а также выяснить вопросы, связанные с выполнением домашнего задания.

7. Подведение итогов урока

Итоги урока подводятся оценкой знаний отвечавших учеков и ответами на вопросы типа:

— Что такое прямоугольник?

— Какими свойствами параллелограмма обладает прямоугольник?

— Какое свойство прямоугольника доказывается в теореме 6.4?

— Сформулируйте признаки прямоугольника.

8. Резервные задания

После выполнения программы отмеченных выше этапов урока и при наличии времени могут быть использованы следующие дифференцированные задания:

— Постройте прямоугольник по двум смежным сторонам.

— Постройте прямоугольник по стороне и диагонали.

— Постройте прямоугольник по диагонали и углу между диагоналями.

— Постройте прямоугольник по заданным серединам всех его сторон.

— Постройте прямоугольник, если заданы точка пересече­ния его диагоналей и две соседние вершины.

** *

Следует отметить, что жестких требований к степени полноты описания конспекта урока не предъявляется. Тем не ми нее, как это следует из реалий и потребностей практики обучения математике, желательно не пренебрегать следующими рекомендациями.

Студенты-практиканты должны составлять конспект каждого урока, обращая особое внимание на подробное освещение содержания изучаемого материала, формулирование вопросов и ответов на них, описание решений всех задач, образцов оформления используемых записей, деятельности учителя учащихся.

Начинающие учителя могут разрабатывать конспекты ни каждому уроку, но систематически, ограничиваясь в остальные случаях составлением планов уроков.

Более опытные учителя математики, как правило, используют в своей работе планы уроков. Конспекты же предстоящих уроков составляются ими в особых случаях: при проведении от крытых уроков или по наиболее трудным вопросам программы.

Безусловно, владение при этом различными подходами | оформлению результатов разработки урока математики сказывается на уровне соответствующих умений учителя. Но не менее важно и то, что открылись новые возможности применение рассматриваемых умений учителя. Они сводятся к тому, что каждому учителю желательно приучиться всякий раз после весьма удачно проведенного урока найти время и в тот же день оформить как можно более подробный его конспект. Это помо­жет собрать по крупинкам собственные находки в педагогической деятельности для систематизации своего опыта работы и совершенствования процесса преподавания математики.

ГЛАВА V