Наглядные пособия и учебное оборудование

В практике обучения математике широкое применение по­лучили следующие виды наглядных пособий и учебного обору­дования:

— плакаты, диаграммы и таблицы;

— демонстрационные и лабораторные модели, приборы, ин­струменты и приспособления;

— раздаточные материалы;

— диапозитивы, диафильмы и транспаранты;

— аудио- и видеозаписи;

— кинофильмы, кинофрагменты и кинокольцовки;

— компьютерные обучающие программы и др.

Указанную последовательность можно использовать при со­ставлении и оформлении перечня имеющихся в наличии нагляд­ных пособий и учебного оборудования, что необходимо сделать перед началом учебного года. Это позволит с учетом степени ос­нащенности кабинета математики, в котором будет работать учитель (состояние классной доски, рабочих мест учителя и уча-< щихся, технических средств обучения, затемнения и т. д.), наметить на предстоящий учебный год:

— когда, где и какие из наглядных пособий и учебного оборудования можно использовать в учебном процессе;

— какие из них и когда должны быть отремонтированы;

— что из наглядных средств и учебного оборудования сле­дует приобрести;

— какие из них можно изготовить своими силами.

Не переоценивая роли наглядных средств и учебного обо­рудования в организации образовательного процесса, тем не менее отметим, что, обладая значительной информационной емко­стью, они помогают на уроке:

— раскрывать содержание и объем новых понятий;

— формировать необходимые знания и умения;

— дифференцировать работу учащихся с учетом их инди­видуальных способностей и уровня математической под- 1 готовки;

— обеспечивать эффективную организацию самостоятель­ной работы учащихся;

— оперативно осуществлять контроль и самоконтроль.

И такая помощь бывает порой весьма существенной, зна­чительно повышающей эффективность использования учебного времени на уроке. Подтверждением тому могут служить много­численные примеры, в том числе:

— использование моделей круга и его равных частей (сек­торов) при разъяснении правила сложения дробей с оди­наковыми знаменателями;

— построение графиков квадратичных функций с помощью шаблонов парабол и их применение при решении задач;

— решение треугольников с использованием микрокальку­лятора;

— применение учебного оборудования и наглядных посо­бий при изучении всего курса стереометрии;

— использование компьютерной поддержки в процессе преподавания математики на различных ступенях обще­го образования и т. д.

В этой связи по каждой учебной теме желательно завести [139] бланки с перечнем средств обучения как фабричного из­готовления, так и самодельных, использование которых в учеб­ном процессе способствует его эффективной организации. Наи­менования пособий фабричного изготовления и их количество на учебное заведение с одним комплектом классов приводится 'Типовых перечнях учебно-наглядных пособий и учебного обо­рудования для общеобразовательных школ» [125,с. 183—190]. Лрекомендации по изготовлению самодельного оборудования, используемого на уроках математики, даны, к примеру, в по­добии [167].

Очевидно, что подготовку наглядных средств и учебного оборудования к урокам следует вести заблаговременно, равно как и оборудование кабинета математики в целом, ибо процесс этот длительный, не прекращающийся: по мере появления но-ныхсредств обучения должны создаваться условия для их ус­пешной эксплуатации. Причем если учитель только приступает К оборудованию кабинета, то рекомендуются такие последова­тельные стадии его организации:

— модернизация классной доски, оборудование ее магнит­ной доской, координатной сеткой и т. п.;

— оборудование помещения приспособлениями для хране­ния и демонстрации таблиц;

— изготовление стеллажей, ящиков, шкафов и т. п., при­способленных для хранения приборов, библиотеки, раз­даточных материалов и другого оборудования;

— оснащение помещения приборами и приспособлениями для демонстрации диафильмов и диапозитивов;

— стационарная установка кодоскопа (графопроектора) в кабинете;

— изготовление специализированной мебели и оснащение рабочих мест учащихся;

— оснащение рабочего места учителя пультом дистанцион­ного управления, аппаратурой, освещением и т. п.;

— оборудование кабинета магнитофоном и комплектом за­писи математических диктантов;

— оборудование кинопроекционной и видеоаппаратурой;

— оборудование аппаратурой для осуществления компью­терной поддержки образовательного процесса.

Организация повторения

Необходимость систематического повторения изученного ма­териала обусловлена как общими задачами обучения, требую­щими прочного и сознательного его овладения, так и самой структурой математических знаний, развивающихся на основе ранее изученных. Ведь не зря же народная мудрость гласит, что повторение — мать учения. Мы остановимся здесь лишь на во­просах отбора материала для повторения.

В психолого-дидактической и методической литературе [45, 135, 184 и др.] выделяют следующие виды повторения: предваряющее, текущее, тематическое и итоговое.

Предваряющее повторение в начале учебного года диктуется необходимостью восстановления опорных знаний и умений, требуемых для дальнейшего изучения математики. Материал для него отбирается в соответствии с требованиями к матема­тической подготовке учащихся [113, 153, 182 и др.]. Так, к на­чалу обучения в V классе учащиеся должны знать:

— наизусть таблицу сложения однозначных чисел и соответствующие табличные случаи вычитания;

— таблицу умножения однозначных чисел и соответствующие табличные случаи деления;

— названия и обозначения единиц важнейших величин — длины (км, м, дм, см, мм), массы (кг, г), площади (м , дм , см²), скорости (км/ч, м/с), времени (ч, мин, с) и уметь:

— читать, записывать и сравнивать числа в пределах миллиона;

— выполнять несложные устные вычисления;

— выполнять письменные вычисления (сложение и вычитание чисел в пределах миллиона; умножение дву- и трехзначного числа на однозначное, двузначное и трехзначное число; деление трех-, четырех-, пятизначного числа на однозначное и двузначное число);

— называть компоненты арифметических действий и читать простейшие числовые выражения (сумма, разность, произведение, частное);

— вычислять значения числового выражения (в том чис­ле выражения со скобками), содержащего три-четыре арифметических действия, на основе знания правила порядка выполнения действий и их свойств;

— решать простые текстовые арифметические задачи, рас­крывающие смысл каждого действия и смысл отно­шений «меньше на...», «больше на...», «меньше в...», «больше в...»;

— решать составные задачи и задачи, для решения кото­рых необходимо использовать знание зависимостей меж­ду важнейшими величинами (скоростью, временем и рас­стоянием при равномерном прямолинейном движении; ценой, количеством и стоимостью товара; площадью пря­моугольника и длинами его смежных сторон и др.);

— распознавать и изображать (на клетчатой бумаге с по­мощью циркуля и линейки) простейшие геометрические фигуры (точку, отрезок, ломаную, окружность, круг, многоугольник);

— измерять длину отрезка, длину ломаной;

— строить отрезок данной длины;

— вычислять периметр и площадь прямоугольника.

Своевременное повторение опорных знаний и умений позволяет учителю уже в начале учебного года выявить пробелы в подготовке учащихся и целенаправленно работать над их устранением в ходе текущего повторения. В него включаются также сведения, связанные с вновь изученным материалом и мате­риалом, необходимым для приобретения новых знаний.

Тематическое повторение применяется с целью углубления И систематизации материала каждой изучаемой темы. На тема­тическое повторение выносятся вопросы исходя из их значимого в структуре материала темы, определяемой программными Требованиями.

В частности, при выборе вопросов для повторения по теме "Сложение и вычитание дробей с различными знаменателями» VI классе можно руководствоваться следующим [153].

Основной целью изучения этой темы является выработка прочных навыков преобразования дробей, сложения и вычита­ния дробей. Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому зна­менателю. При этом рекомендуется не опираться на понятия ИОД и НОК. Умения приводить дроби к общему знаменателю используются для сравнения дробей. При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа. Что касается сложения и вычитания смешанных чисел, которые не находят активного применения в последую­щем изучении курса, то учащиеся должны лишь получить предтавление о принципиальной возможности выполнения таких действий.

Итоговое повторение проводится в конце учебного года. По целям и отбору материала оно сходно с тематическим, однако уровень обобщения материала здесь значительно выше. В этом можно убедиться, рассмотрев, к примеру, цели изучения геометрии в IX классе и соответствующие требования к подготовке учащихся [153, 182 и др.], с помощью которых определяется содержание итогового повторения курса планиметрии.

Целью изучения курса планиметрии является систематическое изучение свойств геометрических фигур на плоскости формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин и курса стереометрии.

В результате его изучения учащиеся должны овладеть следующими умениями, представляющими обязательный минимум;

— изображать геометрические фигуры, указанные в усло­виях теорем и задач, и выделять известные фигуры на чертежах и моделях;

— проводить доказательные рассуждения в ходе решения типичных задач;

— вычислять значения геометрических величин (длин, углов, площадей), применяя изученные свойства и формулы;

— выполнять основные построения циркулем и линейкой, решать несложные комбинированные задачи, сводящие­ся к выполнению основных построений;

— применять аппарат алгебры и тригонометрии в ходе решения геометрических задач;

— использовать векторы и координаты для решения стан­дартных задач (вычисления длин и углов, сложение векторов и умножение вектора на число).

При итоговом повторении осуществляется не только обоб­щение и систематизация, но и углубление знаний по ведущим понятиям, идеям и методам на основе установления логических связей между ними и областей применимости их в самой мате­матике и на практике.

Изложенное приводит к выводу о том, что вопросам орга­низации повторения учитель должен уделять внимание не толь ко при конструировании предстоящего урока. Они должны так же намечаться и соответствующим образом дополняться при годовом и тематическом планировании.

7. Годовое планирование

При организации учебного процесса пользуются различны­ми видами его планирования, среди которых выделяют годовое, тематическое и поурочное. Годовое планирование является наиболее общим видом, с опорой на него разрабатываются те­матическое и поурочное.

Годовое планирование работы по конкретному учебнику и в определенном классе составляется в соответствии с программой и учебным планом, выработанным или используемым педагогическим коллективом общеобразовательного учреждения. Для этого следует ознакомиться также с примерными его раз­работками, публикуемыми в журнале «Математика в школе» и методических пособиях для учителя к школьным учебникам. II них содержится расчасовка, определяющая количество уро­ком, выделяемых как на изучение глав, параграфов и пунктов используемого учебника, так и для проведения контрольных работ.

Если учитель впервые работает по некоторому учебнику и Количество часов, выделяемых ему на изучение этого курса, сов­падает с предлагаемым в примерном планировании, то послед­нее можно включить в содержание годового планирования.

В противном случае примерное планирование подлежит уточнению и корректировке на основе накопленного опыта пре­подавания математики или для приведения в соответствие с ис-пользуемым учебным планом.

В годовое планирование может быть не только включена разбивка учебного материала по урокам, но и указаны календарные сроки их проведения. В таком случае его называют календарным или календарно-годовым. В системе предваритель­ной подготовки учителя к уроку встречаются также полугодо­вое планирование и планирование по четвертям, отличающиеся временными промежутками, отводимыми на предполагаемое изу­чение учебного материала.

Содержание годовых планов, применяемых в практике обучения, весьма многообразно и в совокупности [21, 29, 116 и др.] Включает следующие разделы:

— темы уроков;

— самостоятельные и контрольные работы;

— число часов (уроков);

— даты;

— повторение;

— что пройдено на уроке;

— что задано на дом;

— учебное оборудование;

— учебно-методические пособия.

Результаты проведенных исследований подтвердили целесообразность следующей его компоновки, усматриваемой из приводимого в таблице 3 варианта схемы годового (полугодового или на учебную четверть) планирования.

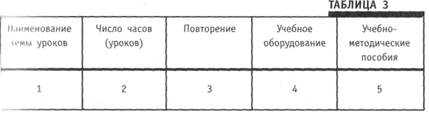
В первом разделе годового планирования записываются те мы уроков и все контрольные работы, что позволяет последовательно спланировать во втором разделе всю учебную нагрузку отводимую на изучение курса. При этом желательно распределить время таким образом, чтобы его хватало на все виды повторения и проведения уроков, посвященных анализу выполи ненных контрольных работ.

В третьем разделе отмечаются темы для предваряющего и итогового повторения, другие же его виды будут учтены в ходе тематического и поурочного планирования.

Перечни используемых на конкретных уроках наглядных пособий и учебного оборудования, а также учебно-методических пособий, отобранных по предложенным нами методикам, вносятся соответственно в четвертый и пятый разделы рассматриваемой схемы.

Не вошедшие в данную схему годового планирования разделы, о которых речь шла выше, либо включаются в содержавние других видов планирования, либо могут быть выявлены Я его помощью. Так, календарный срок проведения каждого конкретного урока вполне определяем с использованием годового планирования, учебного плана, календаря и числа прошедших учебных недель.

Создавая таким образом целостное представление о пред стоящей работе по организации учебного процесса, годовое планирование служит основой для разработки тематического и по урочного планирования.

§ 2. Построение систем уроков по учебным темам

Построением систем уроков по учебным темам завершается работа по конкретизации, уточнению и дополнению годового планирования по учебному предмету. В этих це­лях проводится анализ содержания тем, выявляются межпредметные связи, рассматриваются и подбираются различные системы уроков. Завершается этот этап разработкой тематического планирования, позволяющего своевременно выявить опти­мальные пути достижения целей обучения через систему уро­ков по каждой конкретной теме.

Анализ содержания темы

Вслед за подготовкой к новому учебному году, завершаю­щейся составлением годового плана, учитель переходит к планированию систем уроков по темам. Оно основано на много­стороннем анализе учебного материала темы, предполагающем анализ:

— компонентный (понятийный);

— логический;

— психологический;

— воспитательной значимости учебного материала;

— дидактический.

В методике преподавания математики его вариация предляется последовательностью действий в схеме логико-дидактического анализа темы [91]:

— определение целей обучения;

— логический и методический анализ;

— дидактический анализ.

Образовательные цели изучения темы определяются в программе. Их назначение состоит в предвидении результатов обучи в форме теоретических фактов и умений, а также тех знаний, которые ведут к их достижению в процессе воспита­нии, обучения и развития учащихся.

Логико-методический анализ сводится к установлению логической организации учебного материала темы и к выяснению основных математических и методических идей, заложенных в содержании.

При установлении логической организации учебного материала надо выявить возможный способ построения темы: на соискательной основе, на дедуктивной основе, с использованием ментов дедуктивного подхода. Математические и методические идеи, заложенные в содерне темы, вскрываются при анализе теоретического материал (его основу составляют математические понятия, предложе­ния и доказательства) и задачного материала. При этом устанавливается:

— какие понятия вводятся впервые и даются ли им определения;

— какова связь вводимого понятия с ранее изученными;

— каковы структуры математических предложений;

— верны ли обратные утверждения к встречающимся тео­ремам, и не будут ли они тем самым, например, при­знаками соответствующих понятий;

— как реализуются внутрипредметные связи в курсе мате­матики при изучении этой темы;

— каков объем материала, обязательного для изучения каж­дым учащимся;

— какие утверждения доказываются, а какие лишь разъ­ясняются;

— какие методы используются для доказательств;

— какие новые понятия и предложения содержатся в за­данном материале;

— какие задачи предназначены для введения новых поня­тий и предложений, их закрепления, для связи с изученным и повторения (если такого разделения нет в учебнике);

— какого типа задач недостаточно в учебнике, какими задачами его можно дополнить, какими источниками желательно воспользоваться в этих целях и т. д.

При дидактическом анализе темы осуществляются:

— постановка основных учебных задач и выбор соответствующих учебно-познавательных действий;

— отбор основных методов, приемов и средств обучения;

— определение форм контроля и оценки процесса и результата учебной деятельности учащихся;

— выявление путей дифференциации обучения с учетом возрастных особенностей учащихся, уровня их математической подготовки, способностей и склонностей психологической готовности к самостоятельной деятелености.

Конкретные представления о способах реализации намеченных здесь положений дают материалы следующей главы данного исследования.

Межпредметные связи

Главной педагогической функцией межпредметных связей является формирование у учащихся системы знаний об окружающем мире. Это достигается с помощью совокупности знаний из различных дисциплин, обеспечивающей понимание жизненных явлений, места и роли человека в познании и преобразавании мира.

Актуальность осуществления межпредметных связей обусловлена также современным уровнем развития образования, где новыми импульсами стимулированы процессы интеграции. Они ориентированы на создание и совершенствование интегрированных курсов, раскрывающих мир в целом, преодоление дисцип инарной разобщенности научных знаний и создание условие для полноценного осуществления профильной дифференциации в обучении.

Основными направлениями осуществления межпредметных связей для совершенствования учебного процесса являются:

— усиление системности в компоновке содержания и структуры учебного материала;

— теоретическое обобщение знаний и активизация познавательной деятельности в методах и приемах обучения

— комплексность и сотрудничество учителей разных предметов в формах его организации.

Усиление системности в компоновке содержания и структуры учебного материала через реализацию межпредметных связей осуществляется с учетом программных требований. В частности, в ходе изучения курса алгебры и начал анализа завершается разработка аналитического аппарата, применяемого во всех предметах естественно-математического цикла. А на уроках алгебры и начал анализа постоянно привлекаются сведения из смежных предметов. Различные понятия физики, химии, дачи практического содержания — необходимое условие реа­лизации мировоззренческого потенциала курса. Опора на гео­метрический смысл касательной и механический смысл производной существенно упрощает изложение элементов дифференциального исчисления, помогает добиваться прочного понимания основных фактов.

Как известно, любой метод обучения реализуется в учебном процессе в свойственных ему приемах обучения и их сочетаниях. Применяя же подобранные по педагогической сущнос­ти приемы, обусловленные границами применимости используемого метода обучения, можно активизировать познавательную длительность учащихся по усвоению материалов межпредметного содержания на одном из трех уровней [133]:

1) уровне осознанно воспринятого и зафиксированного в
памяти знания, характеризующегося возможностью учащихся

использовать готовое межпредметное знание;

2) уровне готовности к применению межпредметного знания сходных условиях, по образцу;

3) уровне готовности к творческому применению межпредметных знаний в новых учебных ситуациях.

Так, для объяснительно-иллюстративного метода сущностными будут любые формы предъявления готового знания. Поэтому для организации достижения учащимися первого уровня пения материалов межпредметного содержания могут быть использованы, например, такие приемы обучения: интонационное выделение учителем логически важных моментов предъявляемого материала; инструктаж учащихся по составлению таблиц, схем, по работе с текстом учебника; намек-подсказка, со­держащая готовую информацию; предъявление учащимся переформулированных вопросов, текстов заданий, облегчающих понимание их смысла, и т. п.

Для репродуктивного метода, к примеру, сущностными являются любые формы организации одноразового или многократного воспроизведения учащимися изученного в стандартных условиях или легко опознаваемой близости к образцу. Поэтому любые приемы обучения, преследующие эту цель, можно использовать для организации достижения учащимися второго уроння усвоения материалов межпредметного содержания. Это могут быть наводящие вопросы учащимся, побуждающие к актуализации знаний и способов деятельности; задания учащимся на приведение собственных примеров, подтверждающих правило, свойство и т.д.

А для частично-поискового метода, в частности, в качестве сущностных будут выступать любые формы обучения уча­щихся отдельным этапам творческого поиска. Значит, приемы поучения, направленные на поэлементное усвоение учащимися черт творческой деятельности под руководством учителя, будут Вязаны с достижением третьего уровня усвоения межпредметных знаний. Это и решение нескольких подзадач, выделенных из трудной задачи; и включение учащихся в аргументацию вы двинутой гипотезы; и задания на обобщение фактов межпред метного содержания и т. п.

Наконец, говоря об организационных формах осуществления межпредметных связей, можно выделить интегрированные уроки, лабораторные и практические занятия межпредметного содержания, комплексные экскурсии, межпредметные конференции и т. д. Здесь, как и ранее, не обойтись без сотрудничестве учителей разных предметов, усилиями которых создаются и coвершенствуются необходимые средства реализации межпредметных связей в учебном процессе: вопросы, задания, задачи, наглядные пособия, тексты, учебные проблемы межпредметного содержания и др.

Системы уроков

Система уроков по теме представляет собой согласующуюся с методическими воззрениями учителя последовательности уроков определенных типов, на которых может быть освоен входящий в нее учебный материал. Выбор системы уроков по теме во многом предопределяется результатами анализа содержа ния темы и возможными направлениями реализации межпредметных связей при ее изучении, но не только ими.

Действительно, при изучении, к примеру, материала первых тем курса математики V класса требует особого внимания и решения проблема преемственности между начальным и основным образованием. Она может быть усугублена в случаях не традиционной организации системы начального обучения, в том числе систем, получивших отражение в трудах Ш. А. Амонашвили, Л. В. Занкова, С. Н. Лысенковой и др. Так, построения начального обучения на основе дидактических принципов системы Л. В. Занкова (обучение на высоком уровне трудности, высокий удельный вес теоретических знаний, быстрый темп изучения программного материала, осознание учащимися процесса учения, общее развитие всех обучающихся) требует решения во проса о возможности и особенностях их переноса в средние классы (Вестник образования.— 1994.— № 7.— С. 2—23). Это влечет за собой и внесение определенных изменений в организациионные формы обучения. В занковской системе урок благодаря богатому содержанию, методам, ориентированным на пробуждение самостоятельной мысли и чувства ребенка, характеру взаимоотношений между учителями и учащимися приобретает черты нестандартности, яркости, мобильности. Домашние задания носят разнообразный, часто индивидуальный характер, это снижает возможность перегрузки учащихся. Увеличивается значимость и место экскурсий в учебном процессе. В целом по удельному весу высказываний, конкретных действий на первый план выходят ученики, учитель становится как бы дирижером, усиливается его роль по организации подлинно творческой поисковой деятельности. Другой подход к построению системы уроков может быть связан с реализацией идеи укрупнения дидактических единиц в обучении математике, разработанной П. М. Эрдниевым и Б.П. Эрдниевым [219 и др.]. Укрупненная дидактическая единица — это клеточка учебного процесса, состоящая из логиче­ски различных элементов, обладающих в то же время информационной общностью. Она обладает качествами системности и целостности, устойчивостью к сохранению во времени и быст­рым проявлениям в памяти. Способы укрупнения дидактических единиц включают следующие взаимосвязанные подходы к обучению:

— совместное и одновременное изучение взаимосвязанных действий, операций, функций, теорем и т. п. (в частно­сти, взаимно обратных);

— обеспечение единства процессов составления и решения задач (уравнений, неравенств и т. п.);

— рассмотрение во взаимопереходах определенных и неопределенных заданий (в частности, деформированных упражнений);

— обращение структуры упражнения, что создает условия для противопоставления исходного и преобразованного заданий;

— выявление сложной природы математического знания, достижения системности знаний;

— реализацию принципа дополнительности в системе упражнений (понимание достигается в результате межкодовых переходов между образным и логическим в мышлении, между его сознательным и подсознательным компонентами).

Конструирование системы уроков, на которых реализуется идея укрупнения дидактических единиц, можно, например, иллюстрировать таким планом изучения темы «Решение тригоно­метрических уравнений и неравенств» [60]:

1. Блочное изучение теории и первичное закрепление (5 ч).

2. Проведение зачета по теории (2 ч).

3. Проведение зачета-практикума (1 ч).

4. Уроки углубления знаний и выработки навыков (5ч).

5. Контрольная работа (1ч).

Вариативность компоновки организационных форм обучении зависит и от степени использования учителем накопленпии педагогического опыта. Так, если использовать в качестве способа познания систему погружений, разработанную М. П. Щетининым [218 и др.], то процесс изучения тем курса математики X класса может быть выстроен по следующей схеме.

Первое погружение в течение шести дней в сентябре. После каждой пары уроков математики — разрядка: музыка, хо реография или физкультура. За 32 учебных часа будет пройден курс года (первоначальное знакомство с предметом в целом).

Второе состоится во второй четверти, спустя полтора месяца после первого, третье — через три месяца после второго в начале марта, четвертое — в середине апреля. Каждое продолжается от четырех до семи дней, но суть предмета, область знания, в которые погружается класс, будут уже знакомы. Основные понятия, идеи курса, схваченные в первом погружении, получают дальнейшее развитие, конкретизацию, теоретические вопросы изучаются глубоко, всесторонне. В ноябре выводят уж! знакомые формулы, доказывают теоремы, раскрывают систему понятий. В марте воспроизводят теорию на новом уровне -письменно, устно, с опорой на наглядность, модели... В середи не апреля высший виток усвоения: придумывание задач, опыты, творчество.

При этом в рамках одного дня во все периоды погружение учебная работа строится так, чтобы в различных видах деятельности были задействованы все анализаторы (зрение, слух, моторика), индивидуальные занятия чередуются с групповыми и коллективными, репродуктивные задания — с творческими.

При обращении к методической системе В. Ф. Шаталов! [213, 214 и др.] влияние на выбор системы уроков по теме оказывает каждый из ее элементов: опорные сигналы, контроль! спорт, задачи, повторение, оценка труда. К примеру, специфика работы с опорными сигналами раскрывается при поэтапном изучении теоретического материала темы:

— развернутое объяснение учителя;

— сжатое изложение учебного материала по опорным плакатам, после чего ребята получают листы с опорными сигналами (уменьшенными копиями опорных плакатов [165 и др.]), изучают их, вклеивают в свои альбомы;

— работа с учебником и листом опорных сигналов в домашних условиях;

— письменное воспроизведение опорных сигналов на следующем уроке;

— прослушивание устных ответов товарищей или, еще лучше, ответ у доски.

Трансформация идей В. Ф. Шаталова может привести к такой последовательности уроков по теме [90]:

1. Урок-лекция с подачей опорного конспекта темы. Без доказательства, но мотивированно и связно излагается весь материал темы с привлечением исторических фактов и разнообразных наглядных пособий и ТСО. В течение нескольких уро ков затем ребята сдают письменно, а потом и устно опорные конспекты.

2. Урок типовых задач. Учитель решает для ребят основ­ные задачи темы, дает иерархический список домашнего зада­ния разного уровня оценивания и сообщает срок его сдачи.

3. Урок-семинар. Подготовившиеся ученики и учитель до­капывают все утверждения и теоремы темы. Опорные конспек­ты пополняются конкретным содержанием.

4. Урок парного консультирования. Отрабатываются опор­ные конспекты и теоремы по схеме: сильный — слабый и наоборот.

5. Урок выборочной проверки. Примерно полкласса успевает ответить по опорным конспектам, изученным теоремам и типовым задачам. Это первый срез серьезного контроля.

6. Самостоятельная работа бригадным методом. Посадка в произвольной форме по 2—4 человека (в зависимости от объема работы). К рабочему шуму привыкает даже администрация, лишь бы дети работали. Учитель должен психологически подготовить ребят к работе в группах.

7. Урок-консультация учителя.

8. Урок повторения.

9. Контрольная работа (коллоквиум, зачет по теории, программированный зачет). Это второй срез серьезного контроля.

10. В конце темы сдается домашнее задание (третий срез
Контроля). У ребят две тетради: тонкая — для работы на уроке, толстая — для домашних заданий.

В системе работы учителя математики Р. Г. Хазанкина |24, 208] можно выделить восемь типов уроков, главным из которых является поощрение творческой инициативы как всего коллектива учащихся, так и каждого ученика, органическаяI. индивидуальной и коллективной деятельности, управле­ние общением старших и младших школьников. Это лекция, урок решения ключевых задач, урок обучающих задач, консультация, зачет, урок анализа результатов зачета, контрольная ра­бота, урок анализа результатов контрольной работы.

Приведенные примеры убедительно показывают, что, изучая опыт работы учителей (не только известных, но и работающих рядом в одном учебном заведении), можно найти немало резервов для совершенствования методики отбора системы уроков по каждой теме.

Учителю же, еще не определившемуся в этих вопросах, мы рекомендуем освоить в первую очередь рассмотренную нами ра­нее технологию разработки уроков базовой системы, в которой

аккумулируются наиболее общие структурные элементы совре­менных форм организации обучения. Исходя из этого можно выбирать многочисленные комбинации систем уроков по изучаемой теме с учетом отмеченных ранее условий, поскольку они являются подсистемами или производными подсистемами базо­вой системы уроков математики. В частности, если построение такой подсистемы проводится с учетом специфики учебного ма­териала, например темы «Тригонометрические уравнения», осваиваемой по учебнику алгебры и начал анализа для старшей школы авторского коллектива под руководством академика Российской академии образования Ю. М. Колягина, в непрофилированном классе, где преподавание ведется с примененная методических идей Р. Г. Хазанкина, то это может привести к включению в ее состав:

— уроков ключевых задач;

— уроков обучающих задач;

— урока-консультации;

— урока применения знаний и умений;

— урока-зачета;

— урока анализа результатов зачета.

4. Тематическое планирование

Тематическое планирование служит главным образом выявления оптимальных путей реализации образовательных, воспитательных и развивающих функций учебного процесса в системе уроков по данной теме. Рассматривая различные подходы к составлению тематических планов, можно выделить среди них с определенной долей условности два направления: теоретическое и практическое.

Теоретическое направление разрабатывают коллективы ученых, опытных учителей, методистов и готовят в помощь учителям примерные тематические планы. Они должны раскрывав учителям перспективы их деятельности, создавать представление о расстановке смысловых акцентов и распределении мате риала по урокам, помогать в обеспечении ритмичности учебного процесса, предупреждать неоправданную затрату времени на изучение одних вопросов в ущерб другим, способствовать нормализации нагрузки учащихся и т. д. Содержание такого планирования может быть скомпоновано с опорой на структуру урока, включающего освоение нового материала, и оформлено в виде схемы, раскрывающей следующие положения [70]:

I. Название темы

1. Общая дидактическая цель системы уроков по теме.

2. Тип урока.

3. Общие методы обучения.

4. Оборудование и основные источники информации.

5. Виды контрольных работ по системе уроков.

И. Актуализация знаний

1. Опорные знания и способы действий.

2. Источники повторения.

3. Типы самостоятельных работ.

III. Формирование новых понятий и способовдействия

1. Новые понятия и способы действия.

2. Основные проблемы и типы самостоятельных работ.

IV. Применение (формирование уменийи навыков)

1.Типы самостоятельных работ.

2. Межпредметные связи.

I V. Домашнеезадание

1. Повторение (объем учебного материала).

2. Типы самостоятельных работ.

В практике же обучения математике, как выяснилось в ходе наших исследований, при составлении своих тематических планов (практическое направление) учителя включают в их со­держание лишь отдельные элементы из приведенной схемы. Тем не менее обращение к теоретическому направлению тематичес­кого планирования и в особенности к его содержанию позволя­ет вскрыть ту общую канву, относительно которой развивается вся деятельность учителя как на предварительном, так и на не­посредственном этапе разработки урока. Ею явл<