Вопрос 1: Классификация основных процессов химической технологии.

Вязкость. Напряжение сдвига. Влияние температуры и давления на динамическую вязкость. Ньютоновские и неньютоновские жидкости.

Вязкость (ϻ) = [Па*с] = [м²/с] – св-во Ж, которое приводит к появлению трения между соприкас.слоями текущей Ж, в след.чего эти слои движ. с разными ск-тями.

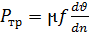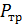( -сила.тр.; ϻ-динамич.вязкость; f-площадь пов.слоя; 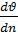– градиент скорости)

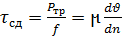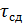( -напряжение сдвига)

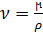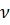( -кинетич.вязкость, 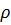– плотность)

Газ: 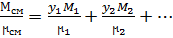(М – мольные массы, у – мольные доли)

Жид: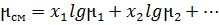

Сусп: С_тв< 10%

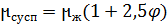
С_тв< 30%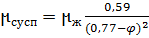

У капель.жид ↑T ↓F_{взаимод} ↓ϻ ; у газов ↑T ↑N_соуд ↑внутр.трение↑ϻ ; не зависит от давления до 10 Мпа

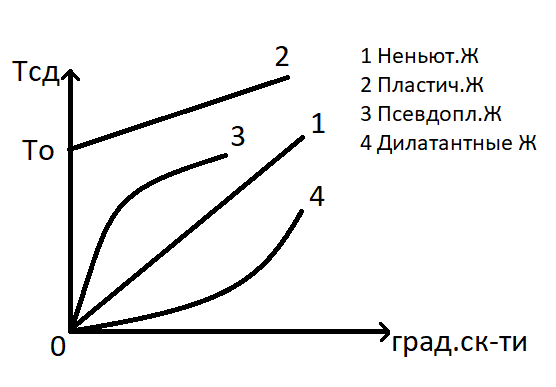
Для неньют.Ж ϻ завис. от условий течения. Зависимость между кас.напряж сдвига и град.скоростипредст графически →

Основные характеристики движения жидкостей: скорость и расход жидкости, гидравлический радиус и эквивалентные диаметр, установившийся и неустановившийся потоки.

а) ск-ть и расход Ж

ск-ть Ж по сечению т/п пост.сечения переменна, наименьш. у стенок и макс. на оси.

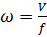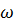( - ск-ть Ж, V – объем.расход, F – попереч.сечение)

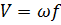- объем.расход

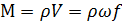[кг/с] ( 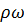– масс.ск-ть) – масс.расход

б) гидравл.радиус, экв.диам.

r_г-отн площади затопл.сеч. т/п к смоч.периметру: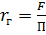

d_э-диам., выраженный через r_г :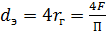

в) уст. и неуст. потоки

Движ. Ж явл. уст-ся, если ск-ть частиц потока, а также все др.влияющих на его движение факторы не изменяются во времени в каждой фикс.точке пр-ва, через кот. проходит Ж

При уст.потоке 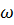может иметь различ. значение в разных точках, но она не изменяется со временем.

Вопрос 8: Уравнение неразрывности (сплошности) потока.

Цель: установить зависимости между скоростями потока, для которого соблюдаются условия сплошности или неразрывности движения (отсутствие пустот).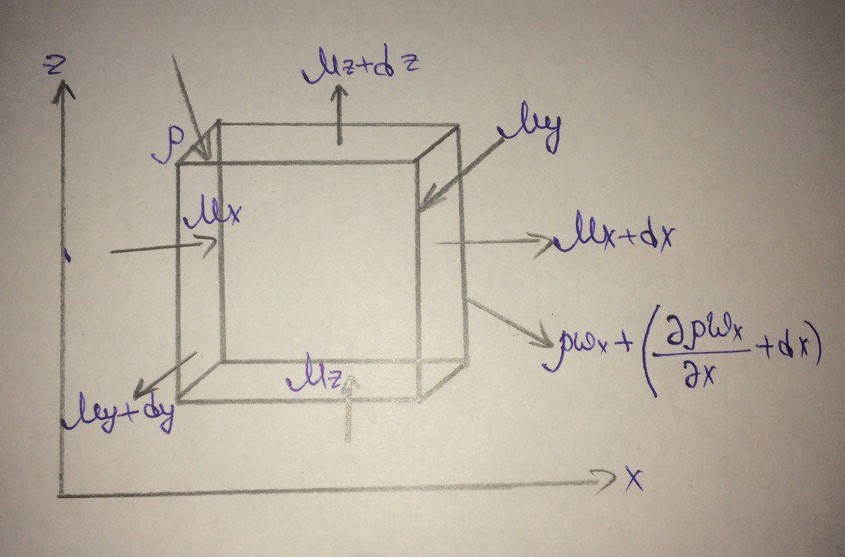

Выделим внутри потока элементарный параллелепипед dV = dxdydz, который перемещается со скоростью w = f(x,y,z).

Изменение массы жидкости в направлении оси х:

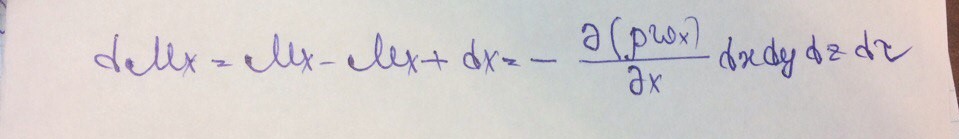
Аналогично получим выражения для оси y, z. Общее изменение массы жидкости в элементарном параллелепипеде:

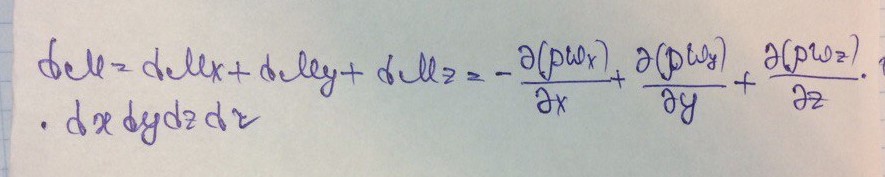
Вместе с тем изменение массы в полностью заполненном жидкостью объеме параллелепипеда возможно вследствие изменения ρ жидкости в этом объеме:

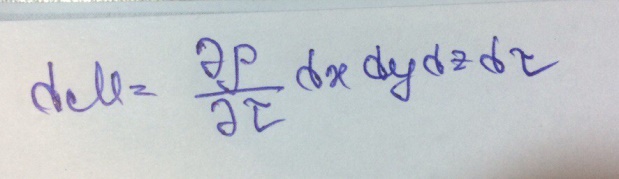
Приравнивая оба выражения для dM, получим дифф. уравнение для неустановившегося движения сжимаемой жидкости:

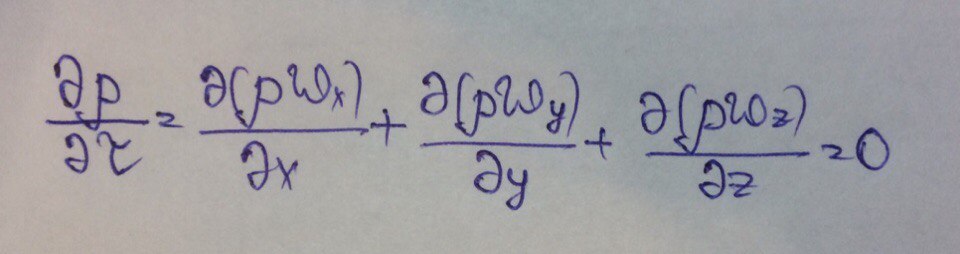
Для капельной жидкости: ρ=const

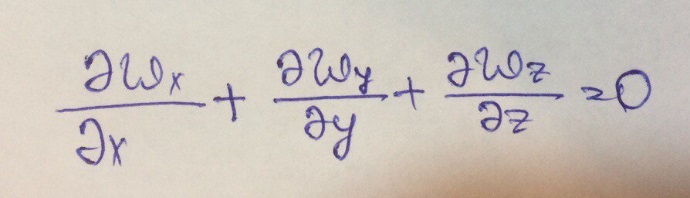
Расчетные формулы в ур-ии неразрывности

В трубопроводе в сечении 1-1 масса жидкости: M₁ = ρ₁w₁f₁, в сечении 2-2: M₂ = ρ₂w₂f₂

При установившемся режиме: M₁ = M₂, ρ₁w₁f₁ = ρ₂w₂f₂

Для капельной жидкости или при ρ=const: w₁f₁ = w₂f₂ или wf=const.

Турбулентный р-м

Re>10⁴, Wср=(0.8-0.9)Wmax

Для турб. режима ж-ти, упорядоченность нарушается, скорость вдоль отдельных частиц становится не постоянной, ????? величина и направление колеблются около средней величины.

2 Дроссельные расходомеры

Для опред. скоростей и расходов ж-ти более широко используются дроссельные приборы: диафрагмы, сопла, труба Вентури

Общей чертой этих устройств является изменение сечения потока, при этом происходит изменение скоростей движения потока и изменяется статическое давление в потоке.

Измерив диафрагмометром перепад давлений перед сечением трубы до его сужения и в месте с сужением, можно вычислить измен. ж-ти между сечениями, а по нему скорость и расход ж-ти.

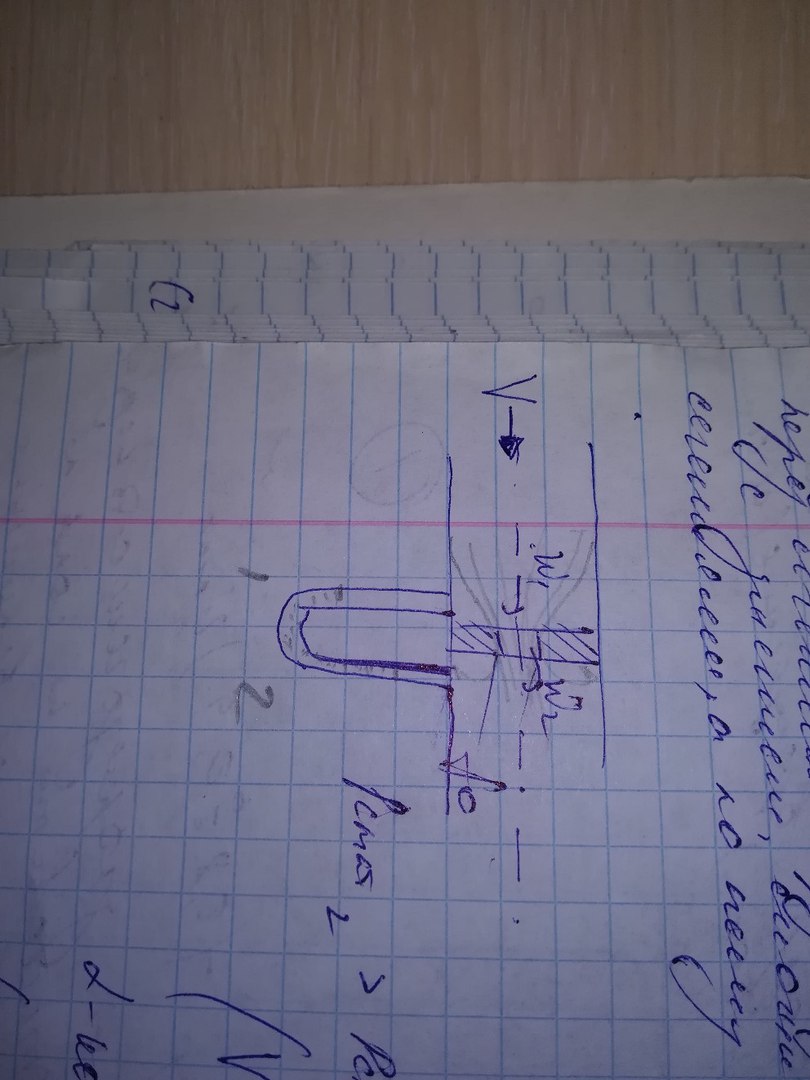
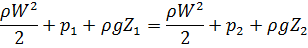
Pстат₂ > Pстат₁

W₂ > W₁

V=α ʄ₀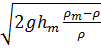

α- поправочный коэф./коэф. расхода =0,6-0,85

ʄ₀-сечение диафрагмы

α= ʄ(Re,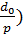

→16. Расчет сетей напорных т/б.

Используют ур-е Бернулли с ур-ем неразрывности потока(ω ,f). При малых скоростях величина hск мала и ее можно не учитывать. В этом случае весь ГД напор (Н) тратится на преодоление гидравлического сопротивления, трения и местных сопротивл.:

;

;

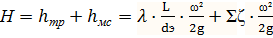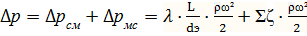В расчетной практике т/б встречается 3 типа задач:

1. Дано: V, d ,L, μ, , e; Найти Н(напор)

1) По заданным V и d рассчитываем скорость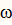

.

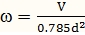2) Зная 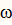,d, μ, - гидродинамический режим течения ж.

.

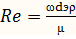3) По знач-ю Рейнольдса и эквивалентной шероховатости d/e, опр-емкоэф-т трения

- потери на трение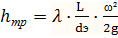

- потери на местное сопротивление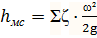

4) опред-ем напор – гидравлические потери напора:

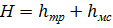
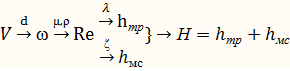
2. Дано: Н, d ,L, μ, , e; Найти V

Порядок расчета проводится при задачи различных значений расходов V в соответствии с алгоритмом решения первой задачи.

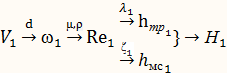
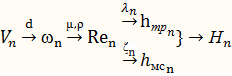
Строим гидравлич-ую характеристику т/б Н=f(V) из графика по известной\высоте напора Н находим искомое знач-е V.

3. Дано: Н, V ,L, μ, , e; Найти d

Решение данной задачи осуществляется по алгоритму аналогично первой задачи при этом, при постоян. расходе V изменяется диаметр т/б; строится график зависимости H от d и по известному значению Н находят искомое d:

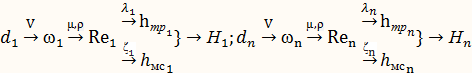
В рез-те решения данной задачи мы получаем dрасчет<d стандартное.

Если т/б состиот из последовательных соед-ых труб различногоd, то следует учитывать, что всем участкам т/б протекает одно и тоже кол-во ж/г. V= ω1*f1= ω2*f2=const. Потери напора равны сумме потерь на всех местных сопротивлениях и потерь на трение по длине т/б. расчеты проводятся с использ-ем гидравлич-ой харак-ки т/б получаемой сложение( по вертикали) гидравлических харак-к отдельных труб.

При параллельном соединении т/б имеют общую точку разветвления и общий узел соед-я. расходы ж-тей в таких случаях распределяются т.о., чтобы гидравлич. потери напора в отдельных линиях были равными.

Вопрос 1: Классификация основных процессов химической технологии.

Классификация может быть проведена на основе различных признаков:

А) В зависимости от основных законов, определяющих скорость процесса.

1. Гидромеханические процессы, скорость которых определяется законами гидродинамики. (перемещение жидкости, сжатие, перемещение газов и т.д.);

2. Тепловые процессы, скорость которых определяется законами теплопередачи (нагревание, выпаривание и т.д.);

3. Массообменные, характеризующиеся переносом одного или нескольких компонентов исходной смеси из одной фазы в другую через поверхность раздела фаз (адсорбция, кристаллизация и т. д);

4. Химические процессы, которые протекают со скоростью, определяющуюся законами хим. кинетики. Вместе с тем скорость хим. процессов существенно зависит от скорости переноса массы и тепла в системе;

5. Механические процессы, описывающиеся законами механики твердых тел (измельчение, транспортирование и т. д.), применяются для подготовки исходных твердых тел и обработки конечных твердых продуктов;

Б) По способу организации (периодические и непрерывные)

1. Периодические процессы характеризуются единством места протекания его отдельных стадий и неустановившимся состоянием во времени (все параметры изменяются в ходе процесса). Все стадии процесса осуществляются в одном аппарате в разное время (произв-во малого масштаба, частая смена ассортимента выпускаемой продукции);

2. Непрерывные процессы характеризуются единством времени протекания всех стадий, непрерывная загрузка исход. материалов и выгрузка конеч. продуктов. Все стадии протекают одновременно в разных точках аппарата (-ов). (многотоннажноепроизв-во). Непрерывные процессы осуществляются в открытых системах;

В) Комбинированные процессы.

1. Непрерывные процессы, отдельные стадии которых проводятся периодически;

2. Периодические процессы, одна или несколько стадий которого проводятся непрерывно;

Вопрос 2:

Общие принципы расчета и анализа процессов и аппаратов.

Связаны с решением след. задач:

1. Определение условий предельного или равновесного состояния системы (направление процесса и его движущая сила);

2. Вычисление расходов исход. материалов и кол-во получаемых продуктов, а также кол-во потребляемой энергии и расхода теплоносителей;

3. Определение оптимальных режимов работы и соответствующей им рабочей поверх-ти или рабочего объема аппаратов;

4. Вычисление основных размеров аппарата;

Материальный и энергетический балансы.

Материальный. По закону сохранения массы, масса поступающих веществ должна быть равна массе веществ, полученных в результате проведения процесса (без учета потерь): ∑G_Н = ∑G_К. С учетом потерь: ∑G_Н = ∑G_К + ∑G_П

Мат. баланс составляют для процесса в целом или для одной стадии.

Энергетический. Кол-во энергии, введенной в процесс, равно кол-ву выделенной энергии. В результате возможно изменение агрегатного состояния веществ.

Частью энерг. баланса является тепловой баланс: ∑Q_Н = ∑Q_К + ∑Q_П (∑Q_{Н –} вводимое тепло). 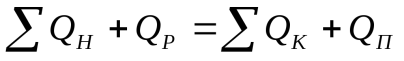, (Q_Р – тепловой эффект процесса). В энерг. балансе учитывается приход и расход всех видов энергии. (по этим данным находят расход энергии на осуществление процесса).

Интенсивность процессов и аппаратов.

Возможность протекания процессов определяется наличием движущей силы, которая: для гидромеханич. процессов определяется Δp; для теплообменных – Δt; для массообменных – Δс. Уравнение любого процесса может быть представлено в общем виде: 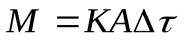.Коэффициент К (коэф. скорости процесса) отражает влияние всех факторов, не учтенных величинами, входящими в правую часть уравнения, а также все отклонения реального процесса от этой упрощенной зависимости. Интенсивность – результат процесса (перенос Q, М и др.), отнесенного к единице времени (ῖ) и единице величины А (раб. поверх-ть): .

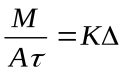или так: K = M / AῖΔ. Интенсивность: R = I / K. (R – гидравлич. сопротивление).

Определение основных размеров аппаратов.

Зная объемный расход (Q) и лин. скорость среды (w) можно определить попереч. сечение идеал. аппарата: S = Q/w (S = πD²/4). D =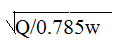

a = F/V(а – поверх-ть, приходящаяся на ед. объема аппарата).

H = V/S(Н – высота аппарата).

V = Qῖ (V – раб. объем, Q – объемный расход, ῖ - периодичность процесса).

Вопрос 3. Гидростатика. Гидростатическое давление. Дифференциальное уравнение равновесие жидкости Эйлера (вывод).

Условие равновесия ж и г (состояние покоя) определяется силами, действующими на некоторый объем ж, при этом делается допущение, что все пространство в данном объеме непрерывно (сплошным образом) заполнено веществом.

Силы, действующие на выделенный объем ж в зависимости от области приложения делятся на внешние и внутренние. По своей природе (по характеристикам действия) делятся на:
а. поверхностные – силы давления, силы внутреннего трения.
б. массовые (объемно-массовые) – сила тяжести, инерции, центробежная.
Ж и г отличаются сплошностью и текучестью (легкая подвижность).

Идеальная ж обладает бесконечно большой текучестью, абсолютно несжимаемая под действием Р, не изменяется плотность под действием Т и не обладает внутренним трением (вязкости). Реальная ж делится на капельную(собственно ж) и упругую(г и пары). Капельные ж практически несжимаемы и обладают очень малым температурным коэффициентом объемного расширения. Объем упругих ж сильно меняется при изменении Т и Р.

Гидростатическое давление возникает в результате действия поверхностных и объемно-массовых сил внутри ж.

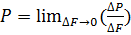– гидростатическое давление в данной точке. Оно одинаково по всем направлениям, ибо в противном случае происходило бы перемещение ж.

Эйлер. (см рис в тетради, пункт 2.1.2) В соответствии с основным принципом статики сумма проекции на оси координат всех сил, действующие на элементарные находящиеся в равновесии = 0. Баланс сил (за «+» направление сил принимают соответствующее направление осей)

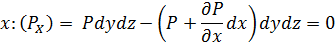
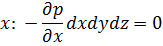
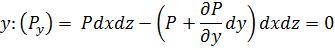
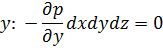
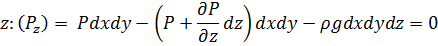
z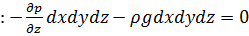

Т.к. 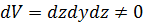, то разделим левую и правую часть уравнений на dxdydz и получим систему дифференциальных уравнений Эйлера для покоящейся ж или находящейся в равновесии.

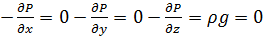, из этого следует что гидростатическое давление меняется только в на оси Z, оставаясь одинаковым во всех точках любой горизонтальной плоскости.

4. Основное уравнение гидростатики. Уравнение Паскаля (вывод).

Основное уравнение гидростатики является интегралом системы Эйлера и дает закон распределения давления во всем объеме покоящейся ж.

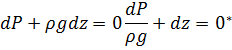
Т.к. для капельных ж ρ=const, то сумма дифференциалов может быть заменена в виде дифференциала суммы: 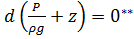, интегрируем выражение: 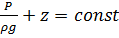- основное уравнение гидростатики, как и: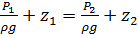

Уравнение Паскаля. Давление в любой точке покоящейся ж в данной горизонтальной плоскости складывается из внешнего давления Р₀ и давления столба ж ρgh: