Расчет на прочность и жесткость статически

Задание 1

Спроектировать привод к конвейеру по заданной схеме. Открытая передача клиноременная, редуктор цилиндрический прямозубый, срок службы привода t = 25000 ч, нагрузка спокойная.

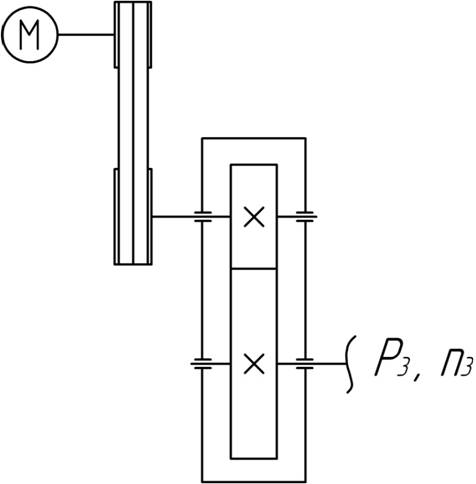
Исходные данные

Величина	Варианты
P3, кВт	1,5	3,0	4,5	6,0	7,5	9,0	10,5		13,5		16,5
n3, мин-1

Задание 2

Спроектировать привод к конвейеру по заданной схеме. Открытая передача цепная, редуктор цилиндрический прямозубый, срок службы привода t = 20000 ч, работа односменная, нагрузка спокойная.

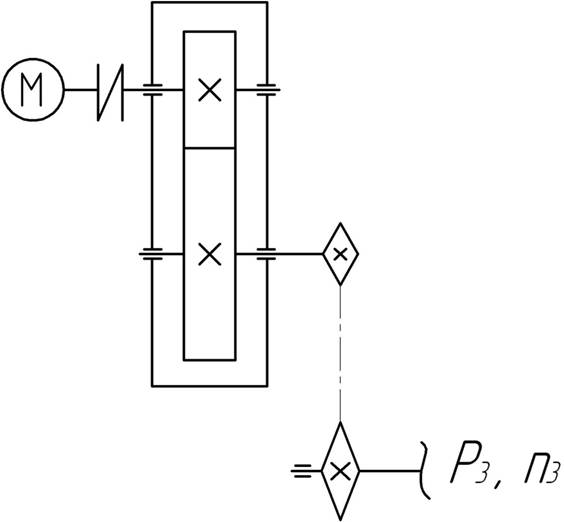
Исходные данные

Величина

Варианты

P3, кВт

n3, мин-1

Задание 3

Спроектировать привод к конвейеру по заданной схеме. Открытая быстроходная передача клиноременная, открытая тихоходная - цепная, редуктор цилиндрический прямозубый, срок службы привода t =30000ч, работа односменная, нагрузка спокойная.

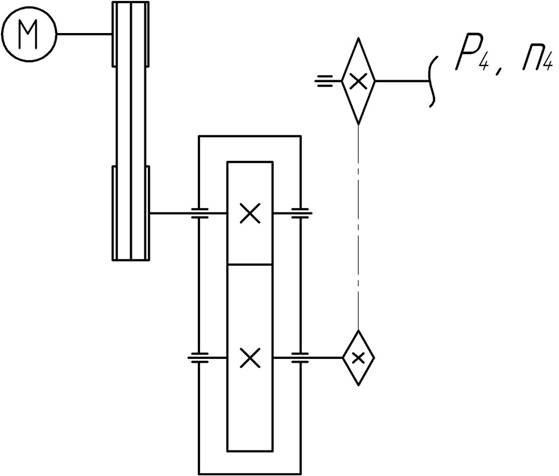
Исходные данные

Величина

Варианты

P4, кВт

n4, мин-1

Задание 4

Спроектировать привод к конвейеру по заданной схеме. Открытая передача клиноременная, редуктор цилиндрический косозубый, срок службы привода t = 25000 ч, работа двухсменная, нагрузка спокойная.

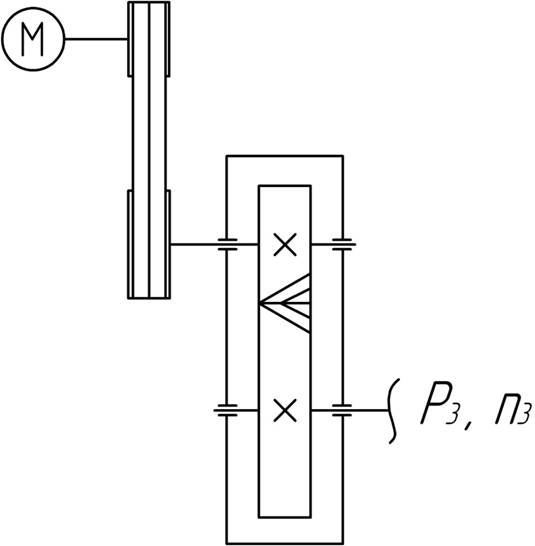
Исходные данные

Величина	Варианты
P3, кВт	1,5	3,0	4,5	6,0	7,5	9,0	10,5		13,5		16,5
n3, мин-1

Задание 5

Спроектировать привод к конвейеру по заданной схеме. Открытая передача цепная, редуктор цилиндрический косозубый, срок службы привода t = 25000 ч, работа двухсменная, нагрузка спокойная.

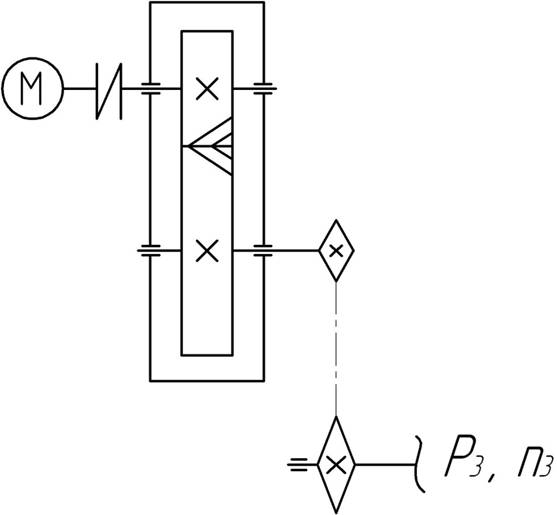
Исходные данные

Величина	Варианты
P3, кВт	2,5	4,5	6,5	8,5	10,5	12,5	14,5	16,5	18,5	20,5	22,5	25,5
n3, мин-1

Задание 6

Спроектировать привод к конвейеру по заданной схеме. Открытая быстроходная передача клиноременная, открытая тихоходная - цепная, редуктор цилиндрический косозубый, срок службы привода t=15000 ч, работа двухсменная, нагрузка спокойная.

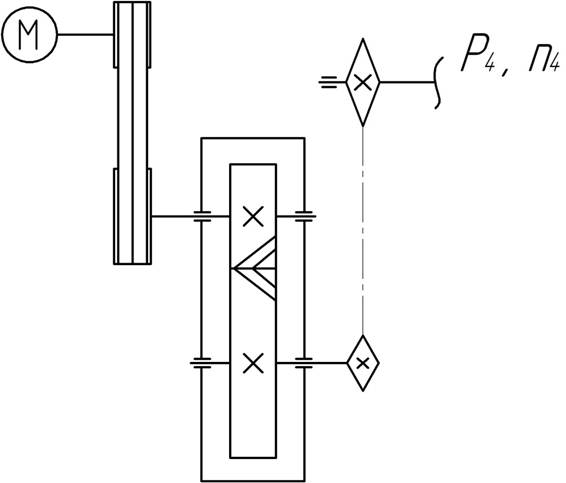
Исходные данные

Величина	Варианты
P4, кВт	3,5	5,5	7,5	9,5	11,5	13,5	15,5	17,5	19,5	10,5	8,5	6,5
n4, мин-1

Пример расчета РГР 1

РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ СТАТИЧЕСКИ

Пример расчета РГР 2

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ

НА ПРОЧНОСТЬ

Для балки, изображённой на рис.1, загруженной сосредоточенными силами Р₁=20кН, Р₂=40кН, равномерно распределённой нагрузкой q=10кН/м и сосредоточенныммоментомМ₀=30кН·мтребуется:

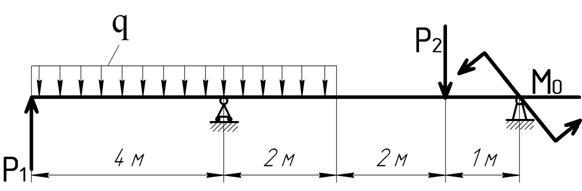
Рис. 1. Схема нагружения балки

1. Начертить ее в масштабе по данным своего шифра;

2. Определить реакции опор;

3. Построить эпюры изгибающих моментов и поперечных сил;

4. Из условия прочности по нормальным напряжениям [s] =160 МПа определить размеры круглого и двутаврового сечений.

5. Сравнить массы полученных балок и выбрать вариант с наименьшей материалоемкостью;

6. Проверить выбранное сечение на касательные напряжения;

Определение реакций опор.

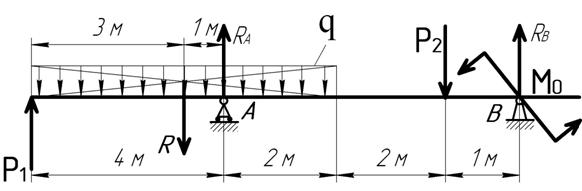
Рис. 2. Схема к определению опорных реакций.

В точках закрепления балки к основанию (точки А и В) прикладываем реакции опор R_A и R_B. Равнодействующая R равномерно распределённой нагрузки q (рис. 2.) определится:

R = q · 6 = 10 · 6 = 60 кН.

Равнодействующая приложена в середине участка: т.е. в трёх метрах от левого края.

Определяем реакции R_А и R_В.

Составляем уравнения статики:

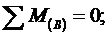
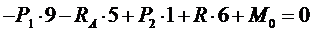
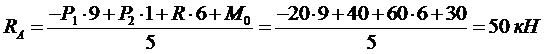
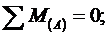
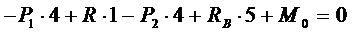
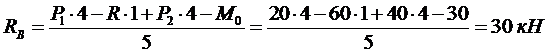
Для проверки записываем уравнение:

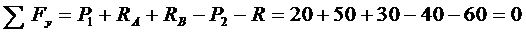
Следовательно, реакции опор R_A и R_B найдены верно.

Первый участок

Длина участка 0 ≤ х₁ ≤ 4,0 м

Рис. 4

По сделанному сечению будут действовать внутренние силы, создающую поперечную (срезающую) силу Q₁ и изгибающий момент M₁. Составим уравнение статики для рассматриваемого участка.

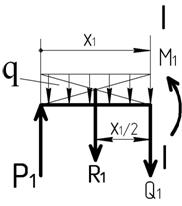
Вместо равномерно распределенной нагрузки можно приложить в середине участка ееравнодействующую R₁ равную произведению нагрузки приходящейся на 1 погонный метр (q) на длину участка на которой она приложена (X₁) - R₁ = q × х ₁.

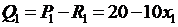
Из полученного уравнения можно сделать вывод, что поперечная сила Q₁ численно равна алгебраической сумме внешних поперечных нагрузок (Р₁ и R₁) лежащих по одну сторону от сечения I-I. Внешние поперечные нагрузки направленные вверх (Р₁) входят в уравнение Q₁ со знаком плюс, а вниз (R₁) – со знаком минус.

Полученное уравнение для Q₁ является прямолинейной зависимостью. Прямую строят по двум точкам. Значение X₁ задаём в начале х₁= 0 и в конце участка х ₁= 4 м.

При х ₁= 0; Q₁ = 20 – 10 × 0 = 20 кН

При х ₁= 4 м; Q₁ = 20 – 10 × 4 = – 20 кН

Для определения изгибающего момента в первом сечении M₁ составляем уравнение статики – сумму моментов относительно центра тяжести первого сечения.

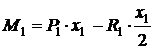
Из полученного уравнения можно сделать вывод, что изгибающий момент М численно равен алгебраической сумме моментов от всех внешних нагрузок (Р₁ и R₁) лежащих по одну сторону от сечения (I-I). Моменты берутся относительно центра тяжести проведённого сечения. Внешние нагрузки действующие относительно центра тяжести проведённого сечения по часовой стрелке входят в уравнение М со знаком плюс, а против часовой стрелки со знаком минус.

После подстановки значений Р₁ и q получим:

M_I = 20·х₁ – 5·х₁²–уравнение параболы.

При х ₁= 0 М₁= 0;

При х ₁ = 4 м М₁= 20 × 4 – 5 × 4² = 0.

Анализируем выражение изгибающего момента на экстремум

.

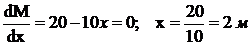Вычисляем значения момента в сечении при х ₁= 2 м.

М₁= 20 · 2 – 5 · 2² = 20 кН·м.

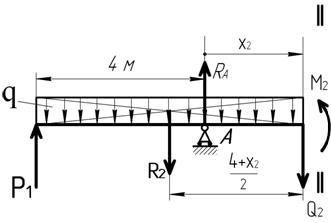
Второй участок.

Длина участка 0 ≤ х ₂ ≤ 2,0 м

Рис.5

Рассмотрим часть балки левее сечения II-II.

Величина равнодействующей R₂ распределённой нагрузки qбудет равна:

R₂ = q · (4+ х ₂).

Расстояние от вектора R₂ до центра тяжести проведённого сечения равно (4+ х ₂)/2.

Q₂ = P₁ + R_A – R₂ = 20 + 50 – 10 · (4+ х ₂) = 30 – 10 · х ₂ – прямая линия

При х ₂ = 0; Q₂ = 30 кН.

При х ₂ = 2 м; Q₂ = 30 – 10 × 2 = 10 кН.

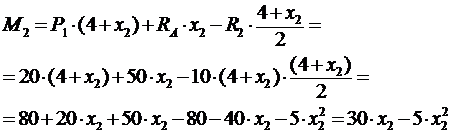
При х ₂ = 0; M₂ = 0.

При х ₂ = 2 м; M₂ = 30 × 2 – 5 × 2² = 40 кН·м.

Третий участок

Длина участка 0 ≤ х ₃ ≤ 2,0 м

Рассмотрим часть балки левее третьего сечения III-III.

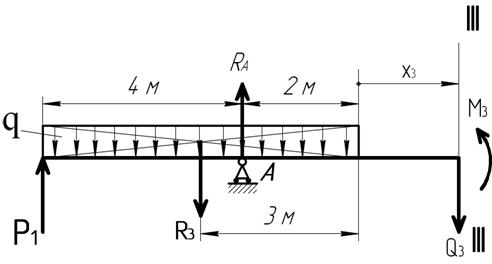
Левее сечения III-III лежит вся распределённая нагрузка, равнодействующая которой R₃ = q × 6. Расстояние от равнодействующей R₃ до сечения III-III будет равно 3+ х ₃.

Q₃ = P₁ + R_A – R₃ = 20 + 50 – 60 = 10 кН

M₃ = P₁ × (4+2+ х ₃) + R_A × (2+ х ₃) – R × (3+ х ₃) =

= 120 + 20 × х ₃ + 100 + 50 × х ₃ –180 – 60 × х ₃= 40 + 10 × х ₃ – прямая линия

При х ₃ = 0; M₃ = 40 кН·м.

При х ₃ = 2 м; М₃ = 40 + 10 × 2 = 60 кН·м.

Четвертый участок

Длина участка 0 ≤ х ₄ ≤ 1,0 м

Рассмотрим часть балки правее сечения IV–IV. В этом случае правило знаков при составлении уравнений для Q и M меняется на противоположное.

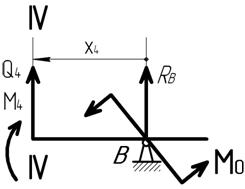
Q₄ = – R_B = – 30 кН

M₄ = – M₀ + R_В × х ₄ = 30 + 30 × х ₄ – прямая линия.

При х ₄ = 0; M₄ = 30 кН·м.

При х ₄ = 1м; М₄ = 30 + 30 × 1 = 60 кН·м.

Строим эпюры поперечных сил Q и изгибающего момента М.

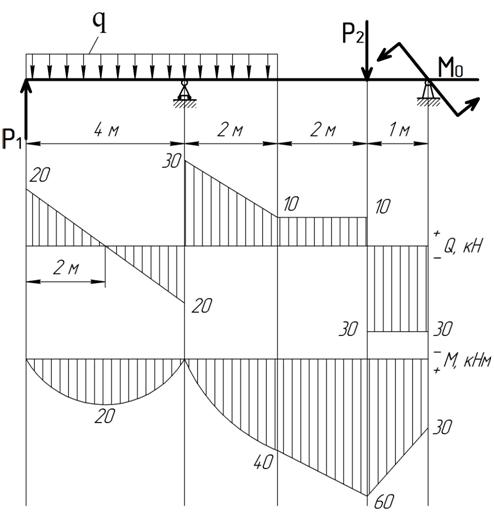
Подбор номера двутавра.

По справочной таблице подбираем № профиля двутавра, имеющего близкое значение осевого момента сопротивления к 400 см³.

Соответствует №27а, у которого W_x = 407 cм³.

Площадь А_д = 43,2 см²

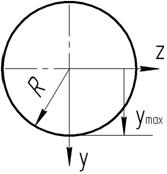
Касательным напряжениям.

Проверку проводим балки с двутавровым поперечным сечением. Наибольшее напряжение определяются по формуле:

Рис. 10

Максимальные напряжения по высоте двутавровой балки будут действовать в волокне расположенном по оси Z.

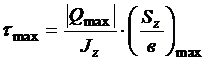
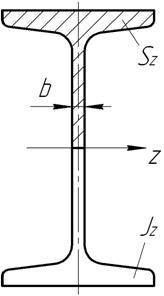
В этой формуле |Q_max| = 30 кН - наибольшая по длине балки поперечная сила. Берется с эпюры |Q_max| = 30 кН.

J_z – осевой момент инерции выбранного поперечного сечения (J_Z = 5500 см⁴). S_Z – статический момент части двутавра относительно оси z (берем со справочника для двутавра №27а), S_Z = 229 cм³.

b – ширина волокна в котором ищется напряжение, b = 6 мм.

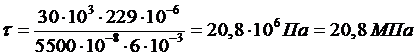
Действующее напряжение (t = 20,8 МПа) меньше допускаемого ([t] = [s]/2 = 80 МПа), следовательно, двутавр №27а по наибольшим касательным напряжениям подходит.

Двутавры

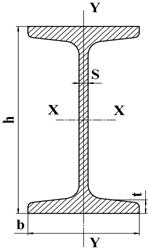
Номер балки	h, мм	b, мм	s, мм	t, мм	Площадь, см2	Масса 1 м, кг	Справочные величины для осей
x-x	y-y
Jx, см4	Wx, см3	ix, см	Sx, см3	JY, см4	WY, см3	IY, см
			4,5	7,2	12,0	9,46		39,7	4,06	23,0	17,9	6,49	1,22
			4,8	7,3	14,7	11,50		58,4	4,88	33,7	27,9	8,72	1,38
			4,9	7,5	17,4	13,70		81,7	5,73	46,8	41,9	11,50	1,55
			5,0	7,8	20,2	15,90		109,0	6,57	62,3	58,6	14,50	1,70
			5,1	8,1	23,4	18,40		143,0	7,42	81,4	82,6	18,40	1,88
18а			5,1	8,3	25,4	19,90		159,0	7,51	89,8	114,0	22,80	2,12
			5,2	8,4	26,8	21,00		184,0	8,28	104,0	115,0	23,10	2,07
20а			5,2	8,6	28,9	22,70		203,0	8,37	114,0	155,0	28,20	2,32
			5,4	8,7	30,6	24,00		232,0	9,13	131,0	157,0	28,60	2,27
22а			5,4	8,9	32,6	25,80		254,0	9,22	143,0	206,0	34,30	2,50
			5,6	9,5	34,8	27,30		289,0	9,97	163,0	198,0	34,50	2,37
24а			5,6	9,8	37,5	29,40		317,0	10,10	178,0	260,0	41,60	2,63
			6,0	9,8	40,2	31,50		371,0	11,20	210,0	260,0	41,50	2,54
27а			6,0	10,2	43,2	33,90		407,0	11,30	229,0	337,0	50,00	2,80
			6,5	10,2	46,5	36,50		472,0	12,30	268,0	337,0	49,90	2,69
30а			6,5	10,7	49,9	39,20		518,0	12,50	292,0	436,0	60,10	2,95
			7,0	11,2	53,8	42,20		597,0	13,50	339,0	419,0	59,90	2,79
			7,5	12,3	61,9	48,60		743,0	14,70	423,0	516,0	71,10	2,89
			8,3	13,0	72,6	57,00		953,0	16,20	545,0	667,0	86,10	3,03
			9,0	14,2	84,7	66,50			18,10	708,0	808,0	101,0	3,09
			10,0	15,2	100,0	78,50			19,90	919,0		123,0	3,23
			11,0	16,5	118,0	92,60			21,80			151,0	3,39
			12,0	17,8	138,0	108,0			23,60			182,0	3,54

Пример расчета РГР 3

Пример расчета РГР 4

РАСЧЕТ ЗУБЧАТОЙ ПЕРЕДАЧИ

Передачи редуктора.

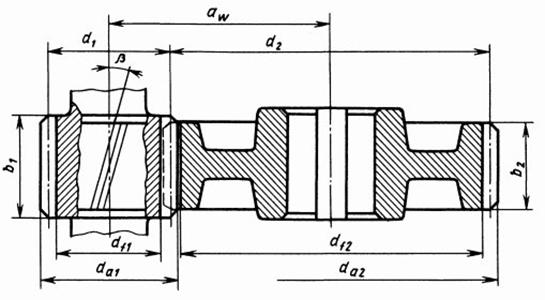
Пример расчета РГР 5

РАСЧЕТ ЦЕПНОЙ ПЕРЕДАЧИ

1. Определим шаг цепи р, мм:

,

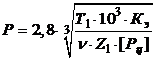где Т₁ – вращающий момент на ведущей звездочке, в нашем случае Т₁ = Т₃= 448 Нм; Кэ – коэффициент эксплуатации, представляет собой произведение пяти поправочных коэффициентов, учитывающих различные условия работы передачи:

К_э = K_д · K_с ∙ K_θ ∙ K_РЕГ ∙K_р (см. табл.10), тогда

К_э = 1 ∙ 1,5 ∙ 1 ∙ 1,25 ∙ 1,25 = 2,34.

Z₁ – число зубьев ведущей звездочки:

Z₁ = 29 – 2 · u,

где u = 2,2 (см. пример расчета РГР 3 «Кинематический расчет привода»), тогда:

Z₁ = 29 – 2 ∙ 2,2 = 24,6.

Принимаем Z₁ = 25.

Полученное значение Z₁ округлить до целого нечетного числа, что в сочетании с нечетным числом зубьев ведомой звездочки Z₂ и четным числом звеньев цепи Lр обеспечит более равномерное изнашивание зубьев.

ν – число рядов цепи.

Выбираем однорядную цепь, тогда ν = 1.

[р_ц] – допускаемое давление в шарнирах цепи, МПа (см. табл. 11), при

ω₃ = 11,5 c^-1, 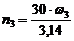= 109,8 мин^-1, [р_ц]=35 МПа.

Определим шаг:

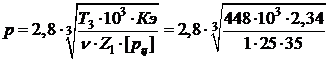= 29,7 мм.

по табл. 12, принимаем p = 38,1мм.

Выбираем цепь приводную роликовую нормальной серии однорядную типа ПР – 38,1 – 12700 (ГОСТ 13568-75).

2. Определим число зубьев ведомой звездочки:

Z₂ = Z₁×u

Z₂ = Z₁∙u = 25 ∙ 2,2 = 55.

Полученное значение Z₂ округляем до целого нечетного числа

Z₂ = 55.

Для предотвращения соскакивания цепи максимальное число зубьев ведомой звездочки ограничено: Z₂ ≤ 120.

3. Определим фактическое передаточное число U_ф и проверим его отклонение и от заданного U:

.

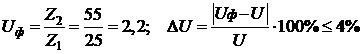
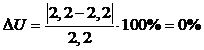4. Определим оптимальное межосевое расстояние, мм.

Из условия долговечности цепи

а = (30…50)p,

где p – стандартный шаг цепи. Получаем тогда:

а_р = а / p = 30…50 – межосевое расстояние в шагах.

5. Определим число звеньев цепи L_р, шт:

.

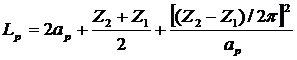Получаем:

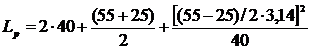= 120,5.

Принимаем L_р = 120.

6. Уточним межосевое расстояние в шагах:

.

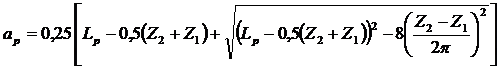Получим численное значение а_р:

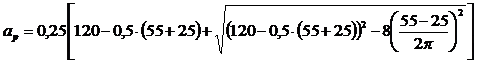=39,71.

Тогда фактическое межосевое расстояние:

а = а_р · p = 39,71 · 38,1 = 1512,95 мм.

Монтажное межосевое расстояние:

а_м = 0,995 · а = 0,995 · 1512,95 = 1505,38 мм.

7. Определим длину цепи L, мм:

L= L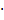_р р

L= L_р 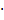р = 120 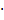38,1 = 4572 мм

8. Определим диаметр звездочек, мм:

Диаметр делительной окружности:

Ведущей звездочки:

.

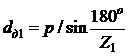Ведомой звездочки:

.

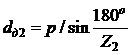Получаем, что:

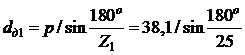= 304,0 мм,

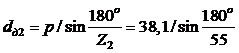= 667,4 мм.

Диаметр окружности выступов:

ведущей звездочки:

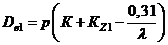
ведомой звездочки

,

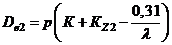где К=0,7 – коэффициент высоты зуба; К_z – коэффициент числа зубьев;

К_Z1 = сtg (180 /Z₁) = сtg (180°/25) = 7,92 – ведущей звездочки;

К_z2 = ctg (180º/Z₂) = ctg (180º/55) = 17,42 – ведомой звездочки;

λ= p / d₁ = 38,1 / 11,1 = 3,43 – геометрическая характеристика зацепления; в этом случае d₁ – диаметр ролика шарнира цепи (см. табл. 12), d₁ = 11,1 мм

Подставив получаем:

D_е1 = p × (К+К_z1 – 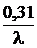) = 38,1× (0,7+7,9 – 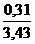) = 324,8 мм

D_е2 = p × (К+К_z2 – 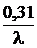) = 38,1× (0,7+17,4 – 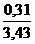) = 689,5 мм.

Диаметр окружности впадин:

ведущей звездочки:

D_i1 = d∂1 – (d₁ – 0,175 × )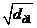

ведомой звездочки:

D_i2 = d∂2 – (d₁ – 0,175× ).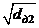

Подставив известные величины определим:

D_i1 = 304 – (11,1 – 0,175 × 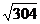) = 295,9 мм

D_i2 = 667,4 – (11,1 – 0,175 × 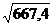) = 660,8 мм.

9. Проверим частоту вращения меньшей звездочки n₁, об/мин

n₁ ≤ [n]₁,

где n₁ – частота вращения тихоходного вала редуктора, об/мин (на этом валу расположена меньшая звездочка).

n₁ = n₃ = 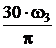= = 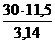109,8 мин^-1;

[n] 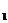= 15 × 10³ / р – допускаемая частота вращения.

[n] 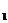= 15 × 10³ / 38,1 = 393,7 мин^-1.

Получаем, что условие выполняется:

n₁ ≤ [n]₁,

109,8 < 393,7.

10. Проверим число ударов цепи о зубья звездочек U, с^-1

U ≤ [U],

где U = 4 × z₁ × n₁ / (60 × Lp) – расчетное число ударов цепи.

U = 4 × z₁× n₁ / (60 × Lp)= 4 × 25 × 109,8 / (60 × 120) » 1,53.

[U] = 508/ р – допускаемое число ударов,

[U] = 508 / 38,1 = 13,33.

Проведем проверку условия:

1,53 ≤ 13,33.

11. Определим фактическую скорость цепи.

V = z₁ × p × n₁ / (60×10³),

где z₁; p; n₁= n₃ определяли ранее.

V = z₁ × p × n₁ / (60×10³) = 25 × 38,1× 109,8 / (60×10³) = 1,74 м/с.

12. Определяем окружную силу, передаваемую цепью F_t, H:

F_t = Р₁ × 10³ / V,

где Р₁ – мощность на ведущей звездочке (на тихоходном валу редуктора), кВт:

Р₁ = Р₃ = Т₃ × ω₃ = 448 × 11,5 = 5,15 кВт.

Определяем окружную силу:

F_t = Р₃ × 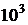/ V = 5,15 × 10³ / 1,74 = 2954,5 Н.

13. Проверим давление в шарнирах цепи Рц, МПа:

Р_ц = Ft × К_э / А ≤ [Р_ц],

где А – площадь проекции опорной поверхности шарнира, мм²;

А= d₁× b₃,

где d₁ и b₃ – соответственно диаметр валика длина и шарнира внутреннего звена цепи, мм (см. табл. 12).

А= d₁× b₃ = 11,1 × 25,4 = 281,94 мм².

[Р_ц] = 35 МПа – допускаемое давление в шарнирах цепи.

Определим давление в шарнирах цепи:

Р_ц = Ft × К_э / А = 2954,5 × 2,34 / 281,94 = 24,56 МПа.

Расчетное давление в шарнире цепи меньше допустимого [Рц] = 35 МПа. Следовательно, износостойкость цепи при заданных нагрузках обеспечена.

14. Проверим прочность цепи S.

Прочность цепи удовлетворяется соотношением:

S ≥ [S],

где [S] – допускаемый коэффициент запаса прочности для роликовых цепей (см. табл. 13) [S] = 8.

S – расчетный коэффициент запаса прочности;

,

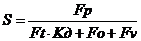где Fp – разрушающая нагрузка цепи, Н (зависит от шага цепи р и выбирается по табл. 12); Ft = 2954,5 Н – окружающая сила, передаваемая цепью; Kд - коэффициент, учитывающий характер нагрузки, равен 1;

Fo – предварительное натяжение цепи от провисания ведомой ветви (от ее силы тяжести), Н;

Fo = K_f × q × a × g,

где K_f – коэффициент провисания; K_f = 6 — для горизонтальных передач; K_f = 3 – для передач, наклонных к горизонту до 40°; K_f = 1 – для вертикальных передач; q – масса 1 метра цепи, кг/м, q = 5,5 кг/м;

а = 1512,95 мм = 1,51 м – межосевое расстояние; g = 9,81 м/c 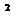– ускорение свободного падения.

Получаем, что:

Fo = K_f × q × a × g = 1× 5,5×1,51× 9,81 = 81,47 H.

Fv – натяжение цепи от центробежных сил, Н;

Fv = q×V²,

где V, м/с – фактическая скорость цепи.

Fv = q×V 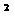= 5,5 × 1,74² = 16,65 Н;

Определим коэффициент запаса прочности:

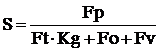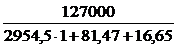= = 41,6.

41,6 > 8 , условие прочности выполняется, так как полученное значение коэффициента запаса прочности больше допускаемого коэффициента запаса прочности.

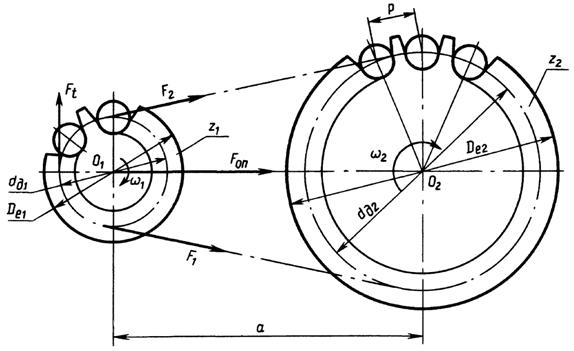
15. Определим силу давления цепи на вал:

Fоп = Kв × Ft + 2 × Fo,

где Kв – коэффициент нагрузки вала (см. табл. 10).

Fоп = Kв×Ft + 2×Fo= 1,15 × 2954,5 + 2 × 81,47 = 3560,5 Н.

Список литературы.

1. Волкова А.Н. Сопротивление материалов: учебник. Для студентов вузов. - М.: Колос, 2004.- 286с.

2. Александров А.В и др. Сопротивление материалов. – М.: Высшая школа, 200.-396с.

3. Ицкович Г.М. и др. Руководство к решению задач по сопротивлению материалов: Учебное пособие. – 3-е изд.-М.: Высшая школа, 2001.-592с.

3. Иванов М.Н. Детали машин. Учебник для студентов высших технических учеб. Заведений – М.: Высшая школа, 2002,-408с.

4. Решетов Д.Н.Детали машин: Учеб. для студентов машиностроительных и механических специальностей вузов. – 4-е изд., перераб. и доп.– М.:Машиностроение,1989. – 496 с.: ил.

5. Колпаков А.П., Корнаухов И.Е.Проектирование и расчет механических передач. – М: Колос, 2000. - 328 с.: ил. – (Учебники и учебные пособия для высш. учеб. заведений).

6. Дунаев П.Ф., Леликов О.П.Конструирование узлов и деталей машин: Учебное пособие для студ. техн. спец. вузов. – 8-е изд., перераб. и доп. – М.: Издательский центр «Академия», 2004. — 496 с.

7. Шейнблит А.Е.Курсовое проектирование деталей машин: Учеб. пособие. Изд-е 2-е, перераб и дополн. – Калининград: Янтар. сказ. 2002.– 454 с.: ил., черт. – Б. ц.

8. Ерохин М.Н., Карп А.В. Детали машин и основы конструирования. М – КолосС, 2005. – 462.:ил. (Учебники и учеб. пособия для студ. высш. учеб. заведений).

Приложения

Таблица 1.

Выбор материала, термообработки и твердости

Параметр	Для передач с прямыми и непрямыми зубьями при малой (Р£2 кВт) и средней (Р£7,5 кВт) мощности;	Для передач с непрямыми зубьями при средней (Р£7,5 кВт)
Шестерня, червяк	Колесо	Шестерня, червяк	Колесо
Материал	Стали 35, 40, 45, 40Х, 40ХН, 35ХМ	Стали 40Х 40ХН, 35ХМ
Термообработка	Нормализация Улучшение	Улучшение + закалка ТВЧ	Улучшение
Твердость	£350 НВ НВ1ср-НВ2ср=20…50	³45 HRCэ £350 НВ НВ1ср-НВ2ср³70
Допускаемое напряжение при числе циклов перемены напряжений NНО; NFО, МПа	[s]НО	1,8 НВср + 67	14 HRCэср+170	1,8 НВср+67
[s]FO	1,03 НВср	370 при m³3 мм	1,03 НВср
310 при m<3 мм

Примечания: 1. В зубчатых передачах марки сталей шестерни и колеса выбрать одинаковыми. При этом для передач, к размерам которых не предъявляют высоких требований, следует применять дешевые марки сталей типа 40, 40Х. 2. Для колес открытых передач большого диаметра (D³500 мм) применить стальное литье (35Л, 40Л, 45Л, 40ГЛ, термообработка – нормализация, улучшение) в паре с кованной шестерней из стали соответствующей марки.

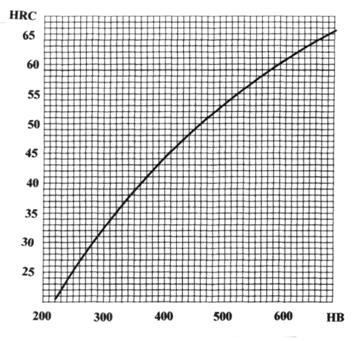
Рис.1. График соотношения твердостей, выраженных в

единицах HB и HRC.

Таблица 2

Механические характеристики некоторых марок сталей для изготовления зубчатых колес и других деталей

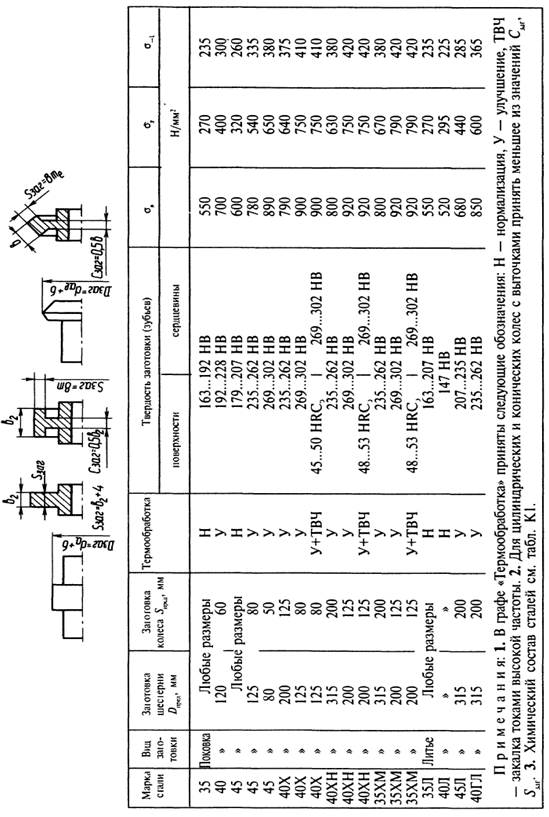
Таблица 3

К выбору допускаемых напряжений для зубчатых колёс

Термообработка	Твёрдость зубьев	Марка стали	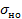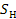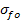, МПа		, МПа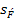
Поверхность	Сердцевина
Нормализация, улучшение	НВ 180-350	40,45;40ХН и др.	2HB+70	1.1	1.8НВ	1.75
Объёмная закалка	HRC 45-55	40,45;40ХН и др.	18HRC+150	1.1		1.75
Поверхностная закалка ТВЧ	HRC 56-63 HRC 45-55	HRC 25-55 HRC 25-55	У6;35ХМ;40Х;40ХН и др	17HRCn+200 17URC+200	1.2		1.75
Сквозная закалка ТВЧ	HRC 45-55	HRC 45-55	35ХМ; 40Х; 40ХН и др.	17НКС+200	1.2		1.75
Азотирование	HRC 55-67 HRC 50-59	HRC 24-40 HRC 24-40	35ХЮА; 38ХМЮА; 40Х; 40ХФА; 40ХНМА		1.2	12HRCсерд +300	1.75
Цементация и закалка	HRC 55-63	HRC 25-40	Цементируемые стали всех марок	23HRC	1.2		1.55
Нитроцементация и закалка	HRC 57-63	HRC 25-40	25ХГМ; 25ХГНМ; 25ХГТ; 30ХГТ; 35Х	23HRCn 23HRCn	1.2	1000 750	1.55
Примечание. 1. HRC2 – твердость поверхности, HRCсердц – сердцевины.

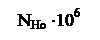
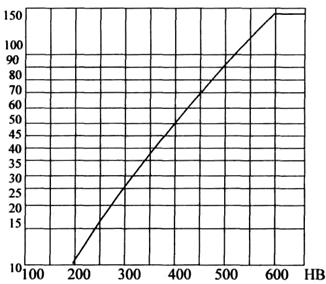
Рис. 2. Зависимость твердости НВ и Nно (базовое число

циклов напряжения)

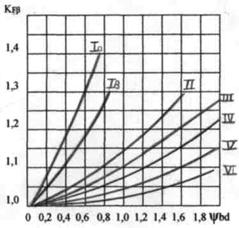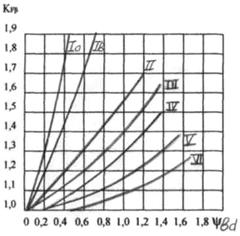
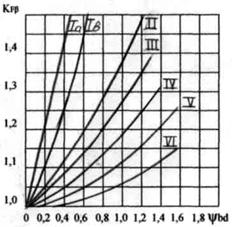
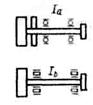
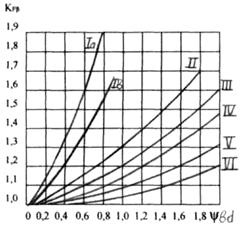При НВ2 ≤ 350. При НВ1 >350 и НВ2 >350.

Рис. 3. Графики для определения коэффициентов КНb и КFb.

Таблица 4.

Степени точности зубчатых передач

Степень точности	Окружные скорости V, м/с вращения колес.
Прямозубых	Непрямозубых
Цилиндрических	Конических	Цилиндрических	Конических
	До 15 »10 »6 »2	До 12 »8 »4 »1,5	До 30 »15 »10 »4	До 20 »10 »7 »3

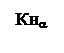
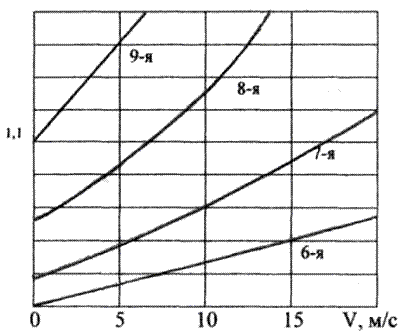
Рис. 4. График для определения коэффициента КНα.

Таблица 5.

Значения коэффициентов KHv и KFv при НВ₂ ≤ 350

Степень точности	Коэффициент	Окружная скорость V, м/с
	KHv   KFv	1,03 1,01 1,06 1,02	1,06 1,02 1,13 1,05	1,12 1,03 1,26 1,10	1,17 1,04 1,40 1,15	1,23 1,06 1,58 1,20	1,28 1,07 1,67 1,25
	KHv   KFv	1,04 1,02 1,08 1,03	1,07 1,03 1,16 1,06	1,14 1,05 1,33 1,11	1,21 1,06 1,50 1,16	1,29 1,07 1,67 1,22	1,36 1,08 1,80 1,27
	KHv   KFv	1,04 1,01 1,10 1,03	1,08 1,02 1,20 1,06	1,16 1,04 1,38 1,11	1,24 1,06 1,58 1,17	1,32 1,07 1,78 1,23	1,4 1,08 1,96 1,29
	KHv   KFv	1,05 1,01 1,13 1,04	1,1 1,03 1,28 1,07	1,2 1,05 1,50 1,14	1,3 1,07 1,77 1,21	1,4 1,09 1,98 1,28	1,5 1,12 2,25 1,35

Примечание: В числителе приведены данные для прямозубых колес, в знаменателе – для косозубых и круговыми зубьями.

Таблица 6.

Коэффициенты форма зуба Y_F1 и Y_F2

z или z v	YF	z v	YF	z v	YF	z v	YF	z v	YF	z v	YF
	4,28 4,27 4,07 3,98		3,92 3,90 3,88 3,81		3,80 3,78 3,75 3,70		3,66 3,65 3,62 3,62		3,61 3,61 3,60 3,60	∞	3,62 3,63

Примечание: Коэффициенты формы зуба Y_F соответствуют коэффициенту смещения инструмента х= 0.

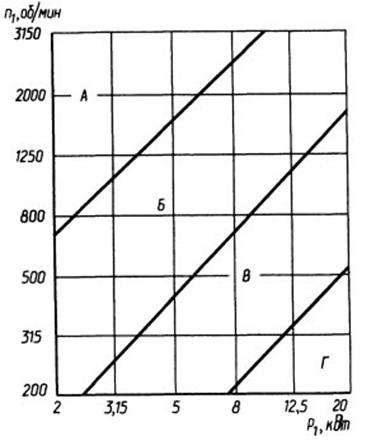
Рис. 5. Номограмма для выбора клиновых ремней

нормального сечения

Рис. 6. Номограмма для выбора клиновых ремней узкого сечения

Таблица 7.

Характеристики и размеры клиновых ремней

Сечение ремня	b0, мм	bp, мм	h, мм	A1, мм	Dmin,мм	q, кг/м	L, мм	T1,Н*м	Тип ремня
Z(0) A(A) B(Б) C(B) D(Г) E(Д) EO(E)   УO УA УБ УВ		8,5   8,5	10,5 13,5 23,5			0,06 0,10 0,18 0,30 0,60 0,90 1,52   0,07 0,12 0,20 0,36	400…2500 560…4000 800…6300 1800…10600 3150…15000 4500…18000 6300…18000   630…3550 800…4500 1250…8000 2000…8000	До 30 15…60 50…150 120…600 450…2400 1600…6000 Свыше 2500   До 150 90…400 300…2000 Свыше 1500	Нормального сечения (ГОСТ 1284.1-89*, ГОСТ 1284.2-89*)     Узкого сечения (ТУ 38-40534; ТУ 38-105161)

Условное обозначение: A₁ – площадь поперечного сечения ремня.

Таблица 8.

Допускаемая приведенная мощность [Р₀], кВт, передаваемая одним клиновым ремнем, узким клиновым ремнем, поликлиновым ремнем с десятью клиньями

Тип ремня	Сечение L0 мм	Диаметр меньшего шкива d1, мм	Скорость ремня r, м/с
Клиновой	О		– – – – – –	0,33 0,37 0,43 0,49 0,51 0,54	0,49 0,56 0,62 0,67 0,75 0,80	0,82 0,95 1,07 1,16 1,25 1,33	1,03 1,22 1,41 1,56 1,69 1,79	1,11 1,37 1,60 1,73 1,94 2,11	– 1,40 1,65 1,90 2,11 2,28	– – – 1,85 2,08 2,27
А		– – – – – –	0,71 0,72 0,74 0,80 0,87 0,97	0,84 0,95 1,05 1,15 1,26 1,37	1,39 1,60 1,82 2,00 2,17 2,34	1,75 2,07 2,39 2,66 2,91 3,20	1,88 2,31 2,74 3,10 3,42 3,78	– 2,29 2,82 3,27 3,67 4,11	– – 2,50 3,14 3,64 4,17
Б		– – – – – –	0,95 1,04 1,16 1,28 1,40 1,55	1,39 1,61 1,83 2,01 2,10 2,21	2,26 2,70 3,15 3,51 3,73 4,00	2,80 3,45 4,13 4,66 4,95 5,29	– 3,83 4,73 5,44 5,95 6,57	– – 4,88 5,76 6,32 7,00	– – 4,47 5,53 6,23 7,07
Узкий клиновой	УО		– – – – – – –	0,68 0,78 0,90 0,92 1,07 1,15 1,22	0,95 1,18 1,38 1,55 1,66 1,80 1,90	1,50 1,95 2,34 2,65 2,92 3,20 3,40	1,80 2,46 3,06 3,57 3,95 4,35 4,70	1,85 2,73 3,50 4,20 4,72 5,25 5,70	– 2,65 3,66 4,50 5,20 5,85 6,42	– – – 4,55 5,35 6,15 6,85
УА		– – – – – –	1,08 1,26 1,41 1,53 1,72 1,84	1,56 1,89 2,17 2,41 2,64 2,88	2,57 3,15 3,72 4,23 4,70 5,17	– 4,04 4,88 5,67 6,3 7,03	– 4,46 5,61 6,0 7,56 8,54	– – 5,84 7,12 8,25 9,51	– – – 7,10 8,43 9,94
УБ		– – – – –	1,96 2,24 2,46 2,64 2,81	2,95 3,45 3,80 4,12 4,26	5,00 5,98 6,70 7,3 7,88	6,37 7,88 9,05 10,0 10,7	– 9,10 10,6 11,9 13,0	– 9,49 11,4 13,1 14,6	– – 11,5 13,3 15,1
Поликлиновой	К