Анализ остатков в дисперсионном анализе
Выражение полной суммы квадратов ошибки (10)  указывает на то, что общее рассеяние наблюдений от среднего объяснятся двумя причинами:
указывает на то, что общее рассеяние наблюдений от среднего объяснятся двумя причинами:
1. Влияние входящих в регрессионную модель регрессоров, оцениваемое как  .
.
2. Влияния, входящие в остаточную сумму квадратов ошибки 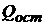 , которые отражают все прочие влияния.
, которые отражают все прочие влияния.
Исследование остаточной суммы квадратов ошибки 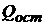 (9) предоставляет возможность подобрать более точную модель и уменьшить стороннее влияние на качество работы модели. Исследовать остатки можно аналитически, графически и комбинируя оба способа. Рассмотрим исследование остатков графическим способом, позволяющим визуально выявить некоторые нарушения и принять меры по их устранению. Остатки
(9) предоставляет возможность подобрать более точную модель и уменьшить стороннее влияние на качество работы модели. Исследовать остатки можно аналитически, графически и комбинируя оба способа. Рассмотрим исследование остатков графическим способом, позволяющим визуально выявить некоторые нарушения и принять меры по их устранению. Остатки 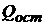 как правило представляют как функцию от:
как правило представляют как функцию от:
1. Предсказанных значений отклика  .
.
2. Некоторых факторов  .
.
3. Времени появления наблюдений.
Часто при построении графиков вводят масштаб, то есть вместо  вводят отношение
вводят отношение  (
(  дисперсия дополнительных опытов (17)). С учетом того, что любая нормально распределенная величина с вероятность 0,95 принимает значение в интервале
дисперсия дополнительных опытов (17)). С учетом того, что любая нормально распределенная величина с вероятность 0,95 принимает значение в интервале  около своего математического ожидания, то и отношение
около своего математического ожидания, то и отношение  тоже будет находиться в интервале
тоже будет находиться в интервале  . В том случае если масштабирование не проводилось, рассуждения относительно видов графика будут аналогичными, просто формы распределения точек на оси не будут ограничены интервалом
. В том случае если масштабирование не проводилось, рассуждения относительно видов графика будут аналогичными, просто формы распределения точек на оси не будут ограничены интервалом  . На рис. 2 представлена зависимость остатков от предсказанных значений отклика
. На рис. 2 представлена зависимость остатков от предсказанных значений отклика  . Здесь точки разбросаны случайным образом в пределах интервала
. Здесь точки разбросаны случайным образом в пределах интервала  , а значит все предположения классического регрессионного анализа выполнены.
, а значит все предположения классического регрессионного анализа выполнены.

Рис. 2. Адекватная зависимость остатков от предсказанных значений отклика
В противном случае (рис. 3) наблюдаются грубые ошибки.

Рис. 3. Неадекватная зависимость остатков от предсказанных значений отклика
В случае выявления грубых ошибок (рис. 3) проводится анализ (аналогично как для  , так и для
, так и для  ) на предмет выявления специфических особенностей изучаемого процесса:
) на предмет выявления специфических особенностей изучаемого процесса:
1. Остатки тенденции (рис. 4). В случае  указывают на неадекватность модели. Характер кривизны показывает, какие члены в модели пропущены. Из рис. 4 видно, что в модели пропущены квадратичные члены. В случае
указывают на неадекватность модели. Характер кривизны показывает, какие члены в модели пропущены. Из рис. 4 видно, что в модели пропущены квадратичные члены. В случае  в модели пропущен квадратичный член
в модели пропущен квадратичный член  .
.

Рис. 4. Графическое представление остатков тенденции
2. Гетероскедастичность наблюдений (рис. 5). Рост прогнозируемого отклика  приводит к падению дисперсии наблюдений. Гетероскедастичность означает неоднородность наблюдений, выраженную в неодинаковой дисперсии случайной ошибки регрессионной модели.
приводит к падению дисперсии наблюдений. Гетероскедастичность означает неоднородность наблюдений, выраженную в неодинаковой дисперсии случайной ошибки регрессионной модели.

Рис. 5. Графическое представление гетероскедастичности наблюдений
3. Направленное изменение остатков (рис. 6). Говорит об ошибках в вычислениях. В случае парной регрессии необходимо добавить в модель дополнительную переменную.

Рис. 6. Графическое представление грубых ошибок в вычислениях
4. Необходимость добавления тригонометрической функции (периодической) (рис. 7).

Рис. 7. Графическое представление необходимости добавления тригонометрической функции
Сначала анализируются функции ошибки от предсказанных значений отклика  с целью выяснения причины неадекватности модели. После выявления причины исследуются функции ошибки от факторов
с целью выяснения причины неадекватности модели. После выявления причины исследуются функции ошибки от факторов  , выявляя тем самым места в модели, к которым необходимо применить модификацию с учетом выявленных недостатков.
, выявляя тем самым места в модели, к которым необходимо применить модификацию с учетом выявленных недостатков.
