Лабораторная работа №5. Проведение классического регрессионного анализа

Лабораторная работа №5. Проведение классического регрессионного анализа

Уравнение регрессии

Измеряемая выходная характеристика представляет собой следующее соотношение (1)

(1)

где

- зависимая переменная, описывающая наблюдаемый процесс;

- независимые переменные, каждая из которых описывает определенный факт, оказывающий влияние на зависимую переменную.

- случайная ошибка.

- неслучайная величина.

В настоящее время существует множество регрессионных моделей, определяемых видом функции , в которой всегда имеются коэффициенты регрессии , вычисление которых производится на основании экспериментальных данных.

Получим на основании (1) уравнение линейной множественной регрессии по отношению к коэффициентам в произвольном виде, но не линейную по отношению к факторам (2).

(2)

Уравнение множественной регрессии (2) характеризует вид зависимости для каждого отдельно взятого опыта из табл. 1. Так как в данном учебном пособии будут рассматриваться только линейные модели и те нелинейные модели, которые можно посредством преобразований привести к виду линейных по коэффициентам. Запишем уравнение (2) в общем виде (3).

(3)

где

- зависимая переменная, описывающая наблюдаемый процесс;

- независимые переменные, каждая из которых описывает определенный факт, оказывающий влияние на зависимую переменную.

- коэффициенты регрессии, вычисляются для каждой и определяют силу и тип взаимосвязи по отношению .

- случайная ошибка (невязки, остаточная переменная), указывающая на долю отклонения модели от реального значения наблюдаемого процесса. Случайная ошибка характеризуется факторами (регрессорами) не учтенными в модели по причине слабого влияния на и в связи с этим удаленные из модели с целью упрощения, либо не известные факторы, что может быть, например, связано с неверностью представленной выборки.

- произвольные функции факторов (регрессоры), не включающие неизвестные коэффициенты . Далее с целью сокращения вместо будет использовано ;

- количество регрессоров функции.

Коэффициенты регрессии играют важную роль при определении взаимосвязи по отношению :

1. Если для знак коэффициента положительный, то наблюдается положительная взаимосвязь между и (повышение приводит к увеличению ).

2. Если для знак коэффициента отрицательный, то наблюдается отрицательная взаимосвязь между и (повышение приводит к уменьшению ).

3. В том случае, когда имеет достаточно большое значение, то говорят о сильной взаимосвязи и .

4. При значении в пределах близких к 0, говорят о слабой взаимосвязи и .

5. - формирует ожидаемое значение в том случае, когда все равны 0.

Так как результаты наблюдений являются случайными величинами, то применив МНК получить истинные значения коэффициентов из модели (3) невозможно. Поступают следующим образом, на основании данных табл. 1 можно получить их оценки . Так как регрессионная модель определяет зависимость среднего отклика рассчитанного для каждого набора факторов без учета случайной ошибки введем обозначение рассчитанного отклика, как (4). Следовательно, далее под будет пониматься отдельно наблюдаемый отклик изучаемого процесса (табл. 1), а под предсказанное значение отклика, служащее оценкой истинного значения .

(4)

Виды регрессии

При помощи регрессионного анализа можно получить два типа моделей:

- Линейная модель регрессии , в том случае, когда функция регрессии линейна относительно параметров модели , то есть коэффициенты должны быть линейными. При этом модель не обязательно линейна относительно .

- Нелинейная модель регрессии (например ) в том случае, когда функция регрессии не линейна относительно параметров .

Различают два типа функциональной зависимости от :

1. Парная регрессия , выраженная как взаимосвязь между и одной независимой переменной .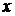

2. Множественная регрессия , выражается как взаимосвязь между и несколькими независимыми переменными .

В зависимости от знака коэффициентов различают следующие виды связи между и каждым регрессором :

1. Положительная взаимосвязь. Если для знак коэффициента положительный, то наблюдается положительная взаимосвязь между и (повышение приводит к увеличению ).

2. Отрицательная взаимосвязь. Если для знак коэффициента отрицательный, то наблюдается отрицательная взаимосвязь между и (повышение приводит к уменьшению ).

3. Сильная взаимосвязь. В том случае, когда имеет достаточно большое значение, то говорят о сильной взаимосвязи и .

4. Слабая взаимосвязь. При значении в пределах близких к 0, говорят о слабой взаимосвязи и .

По характеру отношений между и регрессия может быть:

1. Непосредственная регрессия, когда оказывает прямое воздействие на .

2. Косвенная регрессия, когда оказывает воздействие на через другие факторы.

Лабораторная работа №5. Проведение классического регрессионного анализа