Нагрузка и сжимаемость рабочего тела.

Сжимаемость жидкости и газа в гидравлических и пневматических рулевых машинках дроссельного регулирования с силовым цилиндром обусловлена нагрузкой на штоке силового цилиндра.

Уравнения, характеризующие динамические свойства нагруженной гидравлической рулевой машинки, получают из равенства объемных секундных расходов рабочего тела через золотник и силовой цилиндр и описания работы рулевой машинки как механической системы.

Расходная характеристика золотника рулевой машинки.

При работе рулевой машинки из-за противодействия нагрузки в полостях силового цилиндра возникает разность давлений (рис.3.(2.)):

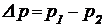; p₁ > p₂ , (30)

под действием которой поршень силового цилиндра перемещается.

Объемный секундный расход жидкости для правого трубопровода равен:

Q₁ 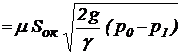, (31)

для левого трубопровода:

Q₂ 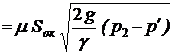(32)

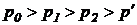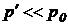Давление жидкости после прохождения через золотник (дроссель) значительно падает: и . Поэтому давление p' можно считать достаточно малым и принять:

p' ≈ 0. (33)

Из условия неразрывности потока жидкости (9) следует: Q₁ = Q₂. Приравняв (31) и (32) с учетом (33), получим:

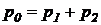. (34)

Из (34) с учетом (30) можно записать:

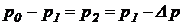. (35)

Добавив в правую и левую части равенства (35) по ( 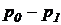) , получим:

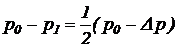. (36)

Тогда, с учетом (36) и (4) уравнение (31) можно представить в следующем виде:

Q₁ 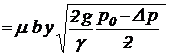. (37)

Для ненагруженной рулевой машинки (М_н = 0, D p » 0) при максимальном отклонении золотника у = y_max максимальный объемный секундный расход жидкости через золотник в соответствии с (37) равен:

Q_{1 max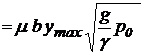} . (38)

Разделив (37) на (38), получим: Q₁ / Q_{1 max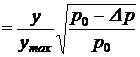} . Откуда, учитывая (16), можно записать:

Q_{зол max} = Q_{1 max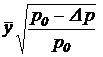} (39)

Уравнение (39) характеризует объемный секундный расход жидкости через золотник при его открытии на величину с учетом действия нагрузки на поршень силового цилиндра. Уравнение (39) - это расходная характеристика золотника нагруженной рулевой машинки с учетом сжимаемости жидкости.

Расходная характеристика золотника нагруженной рулевой машинки, полученная экспериментальным путем, представлена на рис.3.(4а). Из-за действия нагрузки (сомножителя 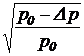) характеристика нелинейная.

Рис.3.(4). Расходные характеристики золотника

(силового цилиндра) нагруженной рулевой машинки

Расходная характеристика силового цилиндра рулевой машинки

В нагруженной рулевой машинке (рис.3.(2)) при перемещении поршня силового цилиндра на величину х₁ под действием давления D p первоначальный объем полости 1 силового цилиндра V₀ изменится до значения V₁ = V₀ + S x₁ .

С учетом (5) значение V₀ равно:

V₀ = S x_max = 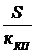δ_max . (40)

Объем V₁ с учетом (40) будет равен:

V₁ = V₀ + 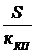δ . (41)

Поскольку жидкость сжимаема, то из-за противодействия нагрузки давление p₁ в полости 1 силового цилиндра должно возрасти на величину D p₁ , чтобы началось перемещение поршня. Под действием этого давления объем сжимаемой жидкости V₁ в соответствии с (27) будет меньше на величину DV₁ :

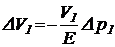. (42)

Поэтому перемещение поршня силового цилиндра будет меньше значения х₁. Для перемещения поршня на величину х₁ необходимо увеличить объем сжимаемой жидкости на величину Δ V₁. Следовательно, 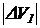- это дополнительный объем сжимаемой жидкости, который при противодействии нагрузки необходимо подать в полость силового цилиндра, чтобы переместить поршень на величину х₁.

Перейдем от малых приращений к производным и запишем (42) в виде:

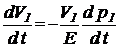(43)

Скорость изменения давления p₁ можно получить из уравнения (36), характеризующего изменение разности давлений в полостях силового цилиндра из-за противодействия нагрузки:

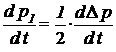. (44)

Подставляя (44) в (43), получим:

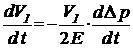(45)

С учетом (41) запишем (45) в следующем виде:

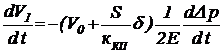. (46)

Таким образом, 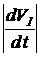- это дополнительный объемный секундный расход, на который необходимо увеличить объемный секундный расход сжимаемой жидкости при возрастании разности давлений в полостях силового цилиндра вследствие противодействия нагрузки, для обеспечения требуемого перемещения поршня силового цилиндра и, в конечном итоге, - требуемого перемещение руля ЛА.

Для ненагруженной рулевой машинки, т.е. без учета противодействия нагрузки (М_н = 0, жидкость несжимаема, т.к. нагрузки нет), при перемещении поршня объемный секундный расход сжимаемой жидкости в полости силового цилиндра Q_СЦ записывают как для несжимаемой жидкости – уравнение (12):

Q₁ = Q_СЦ = 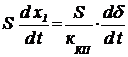. (47)

Следовательно, c учетом сжимаемости жидкости под нагрузкой ее объемный секундный расход, заполняющий полость силового цилиндра и обеспечивающий требуемое перемещение руля, можно запсать в виде суммы объемного секундного расхода несжимаемой жидкости (47) и дополнительного объемного секундного расхода сжимаемой жидкости (46) из-за противодействия нагрузки:

Q₁ = Q_СЦ + 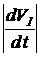= 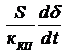+ . (48)

Уравнение (48) характеризует объемный секундный расход сжимаемой жидкости через силовой цилиндр в нагруженной рулевой машинке, требуемый для перемещения руля ЛА на угол d. Уравнение (48) - это расходная характеристика силового цилиндра нагруженной рулевой машинки с учетом сжимаемости жидкости.

Расходная характеристика силового цилиндра нагруженной рулевой машинки представлена на рис.3.(4а).

Из-за противодействия нагрузки (слагаемого 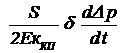) эта характеристика нелинейная и обусловлена дополнительным переменным объемным секундным расходом жидкости (46) в силовом цилиндре.

Механическая характеристика рулевой машинки.

Из условия непрерывности потока жидкости (9) следует:

Q_зол = Q₁ = Q₂ = Q_СЦ = Q

Приравняв (39) и (48) получим:

Q_max 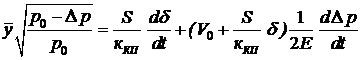(49)

Уравнение (49) объединяет расходные характеристики золотника и силового цилиндра рулевой машинки. Это уравнение нелинейно. Исследовать его трудно, поэтому его линеаризуют.

Линеаризация расходной характеристики золотника рулевой машинки (39) верна в некотором диапазоне 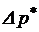изменения давления жидкости 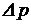- рис.3.(4б).

Аналитическое выражение для линеаризованного уравнения (39) записывают в виде [1]:

Q 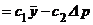, (50)

где: 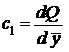- изменение объемного секундного расхода жидкости на единицу относительного перемещения золотника при постоянном перепаде давления: ;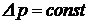

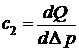- изменение объемного секундного расхода жидкости на единицу перепада давления 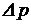при постоянном положении золотника .

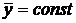Значения коэффициентов 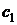и 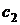для золотников различных конструкций определены экспериментально и приведены в соответствующих справочниках.

Линеаризация уравнения (39) справедлива при малых нагрузках, когда коэффициент запаса рулевой машинки по нагрузке 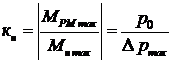велик: к_н = 7…15 или 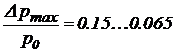, т.е. .

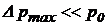При проектировании рулевых машинок беспилотных ЛА с целью снижения массогабаритных показателей запасы по нагрузке принимают малыми:

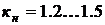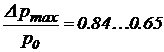( , т.е. 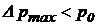). (51)

В этом случае в уравнении (50) значения коэффициентов 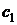и 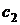определяют по формулам: с₁ = Q_max ; .

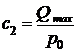Тогда уравнение (39) можно записать в виде:

Q_зол=Q _max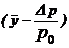 .(52)

Уравнение (52) - линеаризованное уравнение расходной характеристики золотника нагруженной рулевой машинки.

Линеаризация расходной характеристики силового цилиндра рулевой машинки (48) справедлива при малых значениях углов отклонения органов управления ЛА 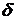. При этом в уравнении (41) можно отбросить по малости слагаемое 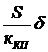. Тогда можно считать, что 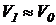и уравнение (48) примет вид:

Q_СЦ 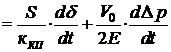. (53)

Уравнение (53) является линеаризованным уравнением расходной характеристики силового цилиндра нагруженной рулевой машинки.

При максимальной скорости отклонения руля 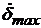из уравнения (47) следует:

Q_{1 max} = Q_max = Q_{СЦ max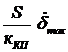} = . (54)

Заменяя в уравнении (49) левую и правую части соответственно уравнениями (52) и (53), с учетом (54) запишем уравнение (49) относительно скорости отклонения руля :

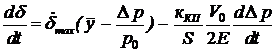, или:

.(55)

Уравнение (55) - это механическая характеристика нагруженной рулевой машинки с учетом сжимаемости жидкости.

Механическая характеристика показывает зависимость установившейся скорости перемещения штока силового цилиндра 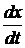,а с учетом кинематической передачи – установившейся скорости отклонения руля ЛА 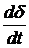от перемещения распределительного устройства рулевой машинки (например, золотника, струйной трубки или другого) на величину при действии со стороны руля на шток силового цилиндра рулевой машинки нагрузки, которая неявно выражена через параметр 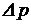, и от развиваемого рулевой машинкой момента (или усилия): .

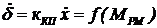Запишем уравнение (55) в другой форме. Для этого введем параметр 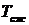. Умножим и разделим правую часть уравнения (55) на и обозначим:

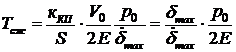. (56)

Постоянная времени 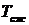, обусловленная сжимаемостью жидкости, характеризует инерционность рулевой машинки – быстроту нарастания перепада давления Δ р на поршне силового цилиндра. Этот параметр оказывает большое влияние на демпфирующие свойства рулевой машинки. Для гидравлических рулевых машинок параметр 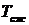составляет сотые и даже тысячные доли секунды, т.к. величина 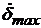достигает значений 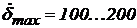град./с и даже значений 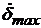≥ 400 град./с (см. также Таблицу 3.(1). раздела «Динамические модели нагруженной рулевой машинки»). 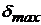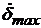Значения параметров и определяют при предварительной оценке динамических характеристик системы стабилизации ЛА или экспериментально.

Умножим и разделим правую часть (55) на 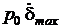. Окончательно, с учетом (40) и (56) уравнение (55) примет вид:

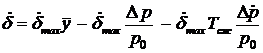(57)

или:

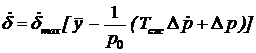(58)

В уравнении (57) первое слагаемое характеризует динамические свойства ненагруженной рулевой машинки, у которой 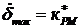- коэффициент передачи (уравнение (17)); второе слагаемое характеризует развиваемое нагруженной рулевой машинкой движущее усилие, выраженное через перепад давления жидкости 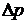в полостях силового цилиндра; третье слагаемое 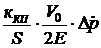характеризует влияние сжимаемости жидкости из-за противодействия нагрузки.

Вид механической характеристики нагруженной гидравлической рулевой машинки показан на рис. 3.(5), где: 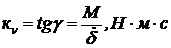– крутизна (жесткость) механической характеристики, необходимая для определения скорости холостого хода руля ЛА 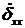и параметров передаточной функции Ф_РМ(s) нагруженной рулевой машинки.

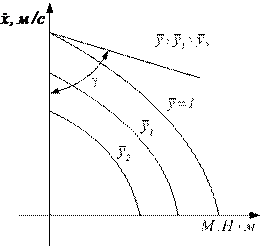
Рис.3.(5). Механическая характеристика нагруженной

гидравлической (пневматической) рулевой машинки

В установившемся режиме работы рулевой машинк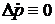и ( ) при 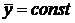из уравнения (57) получают линейное уравнение механической характеристики рулевой машинки:

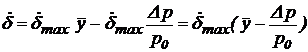. (59)

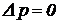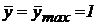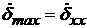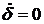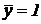При отсутствии нагрузки ( ) и максимальном перемещении распределительного устройства , руль ЛА отклоняется с максимальной скоростью: - угловая скорость холостого хода руля. Если шток силового цилиндра заторможен ( и ), в полости 1 силового цилиндра (рис.3.(2)) давление жидкости максимальное 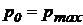, величина движущего усилия, развиваемого рулевой машинкой в заторможенном состоянии, также максимальная, рулевая машинка развивает максимальный момент 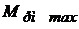(пусковой момент М_п , называемый также тормозным моментом 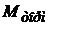). В соответствии с (6):

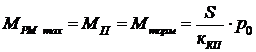(60)

Для пневматических рулевых машинок уравнения, описывающие скорость отклонения руля ЛА с учетом нагрузки, аналогичны уравнениям (57) или (58) для гидравлических рулевых машинок. Но для пневматических рулевых машинок характерны адиабатические процессы, при которых:

Е_газа = æ р, (61)

где: æ - показатель адиабаты (для воздуха æ = 1,4). æ

Значение параметра р, хотя и переменное, но его берут равным 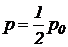. Откуда:

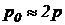. (62)

Тогда из (56) с учетом (61) и (62) получим:

. (63)

После подстановки (56) в (57) или (58) получают линеаризованное уравнение механической характеристики пневматической рулевой машинки.

В нагруженной электрической рулевой машинке механическую характеристику (зависимость угловой скорости отклонения руля ЛА от изменения управляющего сигнала U_я при противодействии нагрузки) определяют из уравнения равенства напряжений: напряжения, подводимого к якорю рулевой машинки U_я , и падения напряжения на обмотке якоря r_я i_я с учетом индуктивности якорной цепи 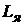и обратной ЭДС рулевой машинки к_е ω. Для рулевой машинки постоянного тока с независимым возбуждением уравнение равенства напряжений записывают в следующем виде:

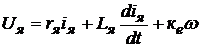, (64)

где: 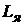, Гн – индуктивность якорной цепи рулевой машинки; обозначения остальных параметров в (64), а также необходимые для дальнейших выкладок уравнения, приведены в разделе «Ненагруженная рулевая машинка».

Запишем уравнение (64) с учетом (20) относительно :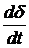

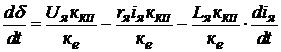. (65)

Перейдем к другой форме записи уравнения (65). Для этого представим приложенное к якорю электродвигателя управляющее напряжение 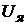в безразмерной форме (25). С учетом уравнений (20) и (24) уравнение (65) запишем в следующем виде:

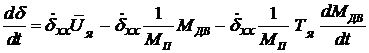, (66)

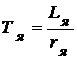, с. (67)

Электромагнитная постоянная времени 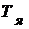электрической рулевой машинки является аналогом параметра 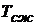гидравлической рулевой машинки.

В уравнении (66) первое слагаемое 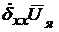характеризует динамические свойства ненагруженной рулевой машинки (без учета нагрузки - инерционности якоря); второе слагаемое 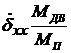характеризует движущий момент, развиваемый рулевой машинкой; третье слагаемое 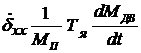характеризует процесс нарастания движущего момента в нагруженной рулевой машинке.

Уравнение (66) можно записать в виде малых приращений Δ М_ДВ :

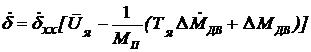. (68)

При 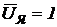, когда 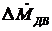= 0 (установившийся режим работы рулевой машинки) из уравнения (68) получают линейное уравнение механической характеристики нагруженной электрической рулевой машинки:

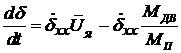. (69)

Линейная механическая характеристика нагруженной электрической рулевой машинки представлена на рис.3.(6.). Такой же вид имеют линейные механические характеристики гидравлических и пневматических рулевых машинок (59).

Рис.3.(6). Линейная механическая характеристика нагруженной

электрической рулевой машинки.

Реальная механическая характеристика нагруженной электрической рулевой машинки ограничена значением предельного момента 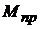, возникающего вследствие реакции якоря и насыщения магнитопровода, когда, начиная с некоторого значения тока якоря, развиваемый рулевой машинкой момент перестает возрастать пропорционально току якоря .

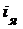Уравнения (66) и (67) по своему виду аналогичны уравнениям (57) и (58).

Таким образом, уравнения механической характеристики рулевых машинок различных типов (61) и (71) имеют структуру, не зависящую от вида источника энергии и типа управляющего устройства, и поэтому являются универсальными уравнениями (за исключением рулевой машинки на горячем газе). ?????

Нагруженная рулевая машинка как механическая система.

В уравнении (57) нагрузка на рулевой машинке была представлена в неявном виде - через разницу давлений на поршне силового цилиндра D p. Выразим параметр D p непосредственно через нагрузку. Для этого опишем динамические свойства нагруженной рулевой машинки как механической системы.

Будем рассматривать все подвижные части рулевой машинки как одно целое. Уравнение динамики нагруженной рулевой машинки получают из уравнения равновесия моментов:

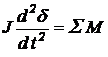- , (70)

где: J, кг×м² - момент инерции подвижных частей рулевой машинки, приведенный к оси вращения руля; ∑ M - сумма моментов, действующих на рулевую машинку:

∑ M = M_РМ - M_н ; (71)

M_РМ , Н×м - момент, развиваемый рулевой машинкой; M_н , Н×м - момент нагрузки:

M_н = M_тр + M_ш ; (72)

M_тр , Н×м - момент трения всех сил в подвижных частях рулевой машинки, приведенный к оси вращения руля: M_тр = к_тр ; к_тр , Н×м/с - коэффициент пропорциональности; M_ш , Н×м - аэродинамический шарнирный момент воздушных, газовых рулей или поворотных крыльев ЛА.

При малых углах поворота руля (рис.3.(2).) момент инерции всех перемещающихся масс гидравлической (пневматической) рулевой машинки с силовым цилиндром, приведенный к оси вращения руля ЛА, равен J = m l² + J_р , где: m, кг – масса поршня и штока рулевой машинки; l, м – плечо кинематической передачи (рычажной системы); J_р , кг∙м – момент инерции руля. Однако инерционность подвижных частей рулевой машинки с силовом цилиндром, приведенная к оси вращения руля ЛА, мала по сравнению с инерционностью руля. Поэтому можно считать: m l² >> J_р .

Поскольку электрическая рулевая машинка развивает относительно небольшие моменты на оси руля, поэтому между рулевой машинкой и рулем ЛА устанавливают силовой редуктор с передаточным отношением i_р >> 1. Момент инерции всех перемещающихся масс электрической рулевой машинки, приведенный к оси вращения руля, равен J = J_я 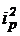+ J_р , в результате чего имеет место неравенство: J_я 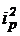>> J_р .

С достаточной точностью шарнирный момент M_ш может быть записан в виде:

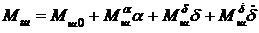, (73)

Составляющие шарнирного момента M_ш – аэродинамические моменты, зависящие от скоростного напора, геометрии органов управления, взаимовлияния ЛА и органов управления 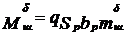; ; 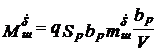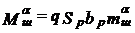могут изменяться в широких пределах в процессе полета.

Некоторые замечания.

1. У осесимметричных ЛА M_{ш 0} ≈ 0 , т.к. несущие и управляющие поверхности имеют симметричный профиль и практически всегда установлены под нулевым углом к оси корпуса ЛА.

2. Центр давления рулей ЛА чаще всего располагают позади оси вращения руля (рули недокомпенсированы). Поэтому знак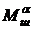и и 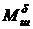отрицательны.

3. Знаки параметров J и 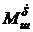всегда отрицательны.

4. Момент трения 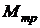целесообразно объединить с аэродинамическим демпфирующим моментом 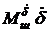и суммарный момент записать по-старому в виде 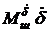. В полете ЛА это слагаемое заметно не изменяется, т.к. обычно 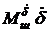<< 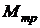, а момент 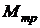изменяется незначительно.

С учетом (73) и сделанных замечаний уравнение (72) запишем следующим образом:

. (74)

Подставляя (74) в (71), уравнение моментов (70) запишем в следующем виде:

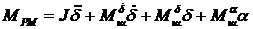. (75)

Уравнение (75) описывает движение нагруженной рулевой машинки как механической системы. Запишем его по-другому, используя понятие тормозного момента 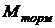. Для этого, умножив и разделив (6) на p₀ , с учетом (60) получим:

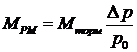. (76)

Подставим (76) в (75) и запишем полученное уравнение относительно :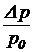

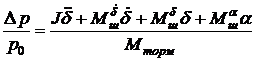. (77)

Уравнение (77) описывает влияние на рулевую машинку нагрузки, выраженную через параметр Δ р .

Динамические свойства нагруженной рулевой машинки.

Объединив (58) и (77), получим систему двух уравнений, определяющую динамические свойства гидравлической рулевой машинки - отклонение руля ЛА 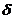в зависимости от перемещения распределительного устройства 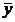с учетом нагрузки на рулевой машинке и с учетом сжимаемости жидкости (рабочего тела) под нагрузкой.

Преобразуем уравнения (58) и (77) по Лапласу:

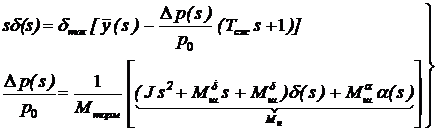. (78)

Системе (78) соответствует структурная схема - рис. 3.(7), где:

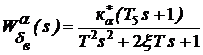; (79а)

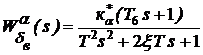; (79б)

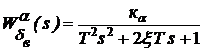; (79в)

; ;

; ;

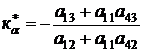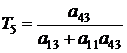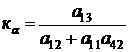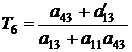79а) ЛА аэродинамических схем: нормальная и «бесхвостка» ( );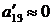

79б) ЛА аэродинамических схем: «утка» и с поворотными крыльями ( ; );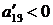

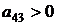79в) маневренные ЛА с малой нормальной силой органов управления ( ; ).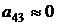

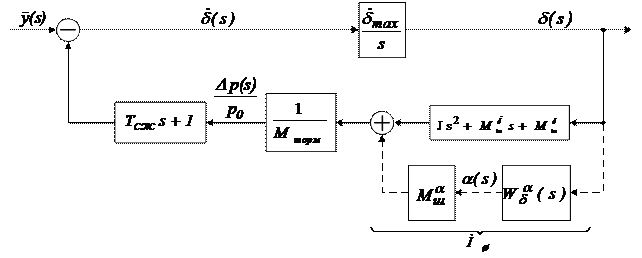
Рис.3.(7). Структурная схема нагруженной рулевой машинки.

Поскольку уравнения, описывающие динамические свойства гидравлических, пневматических и электрических рулевых машинок имеют много общего, а нагрузку для любой рулевой машинки описывают одинаково, то и структурные схемы этих рулевых машинок идентичны.

Коэффициент обратной связи в нагруженной рулевой машинке рис.3.(7) равен:

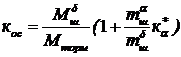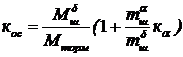или (80)

Из рис.3.(7) видно, что рулевая машинка имеет жесткую обратную связь по шарнирному моменту (80), глубина которой пропорциональна скоростному напору, обратно пропорциональна тормозному моменту и зависит от аэродинамических характеристик ЛА и его органов управления.

Знак пунктирной обратной связи (рис.3.(7).) зависит от знака коэффициента к_α или 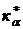в передаточных функциях (79), который, в свою очередь, зависит от аэродинамической схемы ЛА и наличия или отсутствия статической устойчивости ЛА. При отрицательной пунктирной обратной связи рулевая машинка может стать неустойчивой. В этом случае устойчивость рулевого привода обеспечивается соответствующим выбором параметров обратной связи рулевого привода.

При выполнении условия 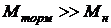, что соответствует выполнению условия (А), нагрузкой можно пренебречь, считая 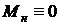. Тогда обратная связь в рулевой машинке исчезает, и динамические свойства рулевой машинки соответствуют передаточным функциям ненагруженной рулевой машинки (18):

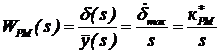и .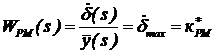

Из сравнения (18) и (78) видно, что динамические свойства нагруженной и ненагруженной рулевых машинок различны.

Определим передаточную функцию нагруженной рулевой машинки .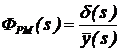

Для удобства анализа динамических свойств нагруженной рулевой машинки преобразуем структурную схему рис.3.(7) к виду, показанному на рис.3,(8).

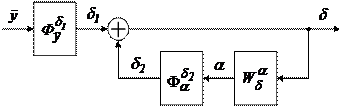
Рис.3.(8). Преобразованная структурная схема рулевой машинки

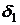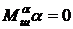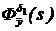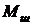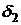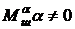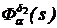
На рисунке: - угол отклонения рулей ЛА при ; - передаточная функция рулевой машинки с обратной связью по шарнирному моменту ; - угол отклонения рулей ЛА, обусловленный влиянием составляющей шарнирного момента ; - передаточная функция замкнутого контура рулевой машинки с обратной связью по шарнирному моменту для входного воздействия α - рис.3.(7).

Передаточную функцию 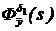определяется из рис.3.(7) при :

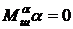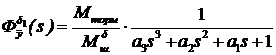, (81)

где: ; ; .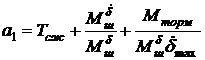

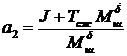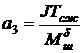Передаточную функцию рулевой машинки 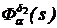можно определить из рис.3.(9) при .

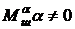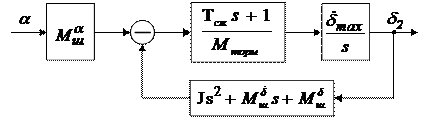
Рис.3.(9). К расчету передаточной функции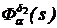

Для упрощения процедуры получения передаточной функции 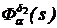преобразуем структурную схему рис.3.(9) к виду, представленному на рис.3.(10).

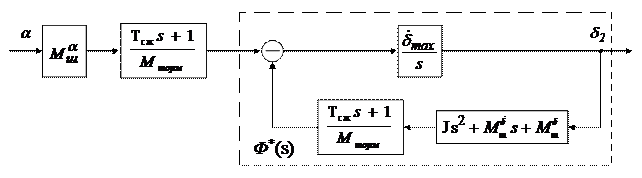
Рис.3.(10). Преобразование структурной схемы рис.3.(9)

На рис.3.(10) передаточная функция 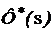аналогична передаточной функции (81): 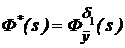. Тогда:

.

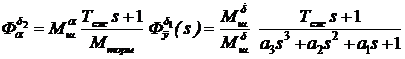Передаточная функция нагруженной рулевой машинки (рис.3.(8)), полученная с учетом проделанных преобразований, равна:

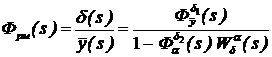. (82)

Динамические модели нагруженной рулевой машинки.

Модель 1. Система уравнений (78) и структурная схема рис.3.(7), или передаточная функция (84), описывающие динамические свойства нагруженной рулевой машинки, достаточно сложны. Для расчёта систем стабилизации на этапах Технических Предложений и Эскизного Проектирования, при качественной оценке динамических свойств нагруженной рулевой машинки пользуются её упрощёнными моделями. В зависимости от степени упрощения системы (78) модели нагруженной рулевой машинки могут быть различны.

Модель 2. Если можно пренебречь составляющей шарнирного момента 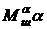, то структурная схема нагруженной рулевой машинки может быть представлена рисунком 3.(7). без пунктирной обратной связи, а её передаточная функция запишется в виде (81).

Модель 3. Если можно пренебречь инерционным (динамическим) и демпфирующим моментами нагрузки (считая, что в (81) 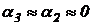), то структурная схема рулевой машинки будет соответствовать рис.3.(8), где: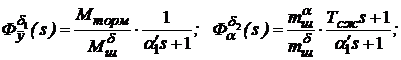

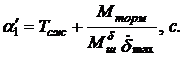
Модель 4. Без учета сжимаемости рабочего тела нагруженную рулевую машинку можно представить структурной схемой, показанной на рис.3.(11), где коэффициент жесткой обратной связи по нагрузке к_ос определяется по формуле (80).

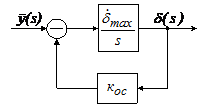
Рис.3.(11). Структурная схема нагруженной

рулевой машинки без учета сжимаемости рабочего тела.

Передаточная функция нагруженной рулевой машинки запишется в следующем виде (гидравлическая рулевая машинка):

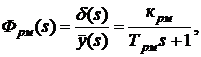, (83)

где: .

Модель 5. Чаще всего основным моментом нагрузки на органах управления ЛА является шарнирный (позиционный) момент 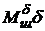. Тогда, пренебрегая моментам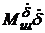и , и 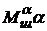, структурную схему нагруженной рулевой машинки можно представить рис.3.(12), где звено с передаточной функцией ( 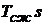+1) учитывает сжимаемость рабочего тела.

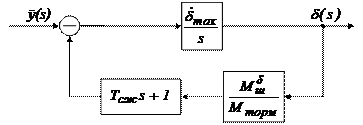
Рис.3.(12). Структурная схема рулевой машинки,

нагруженной шарнирным моментом.

С учётом (51) сделаем некоторые преобразования. Поскольку 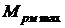= = 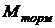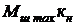; 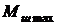= 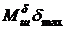, а коэффициент нагрузки рулевой машинки к_н мал:

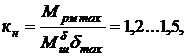то Тогда:

для гидравлической рулевой машинки (56) 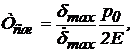с;

для пневматической рулевой машинки (63) 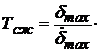1/æ, с;

для электрической рулевой машинки (67). 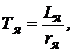с.

Передаточная функция нагруженной рулевой машинки с учётом сжимаемости рабочего тела соответствует (83) с параметром: к_рм = δ_max к_н;

для гидравлической рулевой машинки:

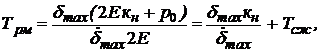с; (84)

для пневматической рулевой машинки:

Т_рм = (1 + æ к_н)Т_сж , с; (85);

для электрической рулевой машинки:

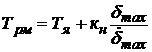, с. (86)

В таблице 3.(1) для рулевых машинок различных типов приведены результаты расчета их основных параметров по полученным формулам в зависимости от вариантов исходных данных.

К расчёту параметров рулевых машинок. Таблица 3.(1).

Тип рулевой машинки	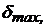град.	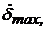град./с	кн		крм град.	Тсж,с Тя, с	Трм, с
Исходные данные	Результаты расчёта
Гидравлическая	±15