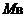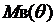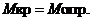Динамическая остойчивость судна.
В ряде случаев судоводителю приходится обращаться к вопросам динамической остойчивости судна. Конечно, в этих случаях судоводитель не решает сложных задач динамики судна – эта область деятельности ученых и исследователей в области теории судна. Но при решении отдельных задач, например при определении динамического крена, при определении предельных значений восстанавливающего момента, после которых судно опрокидывается, и при проверке соответствия параметров остойчивости принятым международным нормам без вопросов динамической остойчивости, хотя бы даже в упрощенной постановке, не обойтись.
Рассмотрение динамики наклонения судна в поперечной плоскости на этом уровне допустимо без учета инерции судна и потерь энергии на взаимодействие с жидкостью. В такой постановке достаточным оказывается использование понятия механической работы, совершаемой кренящим и восстанавливающим моментами, и сопоставлением их величин между собой.
Прежде чем перейти к специальным средствам теории динамической остойчивости, рассмотрим случай динамического накренения судна под действием ударной нагрузки от внезапного шквалистого ветра, пользуясь диаграммой статической остойчивости.
Предположим, что на плавающее без хода на поверхности спокойной воды судно внезапно обрушивается со стороны борта ветровой шквал. Этот шквал характеризуется возникновением ветровой нагрузки на надводной части судна и приводит к появлению внезапно действующего кренящего момента, зависимость плеча кренящего момента во времени представлена на Рис.14.
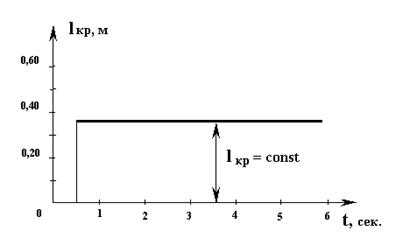
Рис.3.13. Плечо кренящего момента от шквалистого ветра.
Можно с некоторой погрешностью считать, что величина этого кренящего момента слабо зависит от крена судна, т.е. считать его по крену постоянной величиной Мкр (θ) = const. Графическая зависимость такого кренящего момента, помещенная на диаграмму статической остойчивости, выглядит как горизонтальная линия с ординатой, равной величине этого момента (Мкр = М*кр), (Рис. 3.14).
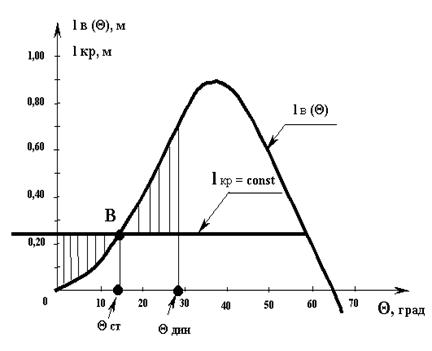 |
Рис.3. 14. Крен судна от действия шквала.
Теперь, если постараться проследить процесс наклонения судна на ДСО, от момента времени, когда восстанавливающий момент еще был равен нулю, то по мере развития (нарастания) угла крена судно будет разгоняться по угловой скорости вращения относительно продольной оси ОХ и приобретать инерцию. Дойдя на ДСО до точки пересечения обоих графиков (точка В на Рис. 3.14) судно не остановится и будет по инерции крениться дальше.
После точки В разница между обоими действующими моментами становиться больше в пользу восстанавливающего момента (∆М = Мв – Мкр > 0), следовательно, этот результирующий момент будет совершать работу, пытаясь остановить его накренение. По-видимому, процесс динамического наклонения судна прекратится в момент времени, которому будет соответствовать равенство работ, совершенных каждым из моментов на своем пути. Поэтому в качестве критерия (меры) динамической остойчивости принимается работа восстанавливающего момента.
Поскольку в механике работа при вращении тела вычисляется как произведение момента на угловой путь (в нашем случае это текущий угол крена судна). Для постоянного момента его работа вычисляется как произведение кренящего момента на угловой путь.
Для переменного по углу крена восстанавливающего момента работа вычисляется по общей формуле механики с использованием операции интегрирования переменного восстанавливающего момента по углу крена:
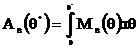 (3.11)
(3.11)
Однако, величина работы в данном случае сама оказывается переменной величиной, т.к. зависит от конечного угла наклонения судна θ = θ*.
В судовых расчетах динамической остойчивости широко используется аналогия между величиной работы и площадью под графиком восстанавливающего момента. В данном рассмотренном случае удобно использовать подобную трактовку для нахождения момента окончания наклонения судна под действием шквала и соответствующий этому моменту динамический угол крена. Этот угол крена может быть найден на Рис.3.9 путем взаимного подбора площадей под обоими графиками до их равенства.
Можно сделать вывод о том, что причиной больших динамических отклонений судна (это видно из сравнений крена θв и θgпри одной и той же величине кренящего момента) является первоначальное «запаздывание» величины восстанавливающего момента, который нарастает постепенно от нуля, и его величина пока меньше величины кренящего момента. За это время, подходя к точке В, судно накапливает инерцию вращения, которую потом ему же самому приходится гасить с помощью увеличившегося к этому времени восстанавливающего момента. Результат этого процесса – значительно большие углы динамического крена по сравнению со статическими, либо даже опрокидывание судна.
Попутно здесь же можно сразу определить тот предельный кренящий динамический момент, действие которого судно уже удержать не сможет, обладая данной остойчивостью и ДСО.
Такой предельный момент называется опрокидывающим моментом (Мопр). Его значение находят на ДСО способом последовательных приближений, постепенно увеличивая величину кренящего момента (подбором более интенсивного шквала); наступает момент расчета, когда для площади под графиком кренящего момента Мкр (θ) уже не найдется равной по величине площади под графиком ДСО
|
 |
| |||
|
|
|
 |
|
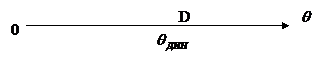 |
Рис.3.15
На Рис.3.15 показано нахождение динамического кренящего момента равного опрокидывающему. Как указывалось выше, работа кренящего момента равна произведению величины момента на величину углового перемещения 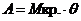 и геометрически интерпретируется площадью прямоугольника ОАСD. Работа же восстанавливающего момента в соответствии с формулой (3.11) геометрически представляется в виде площади, ограниченной кривой
и геометрически интерпретируется площадью прямоугольника ОАСD. Работа же восстанавливающего момента в соответствии с формулой (3.11) геометрически представляется в виде площади, ограниченной кривой 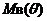 , осью
, осью 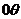 и перпендикуляром восстановленном из точки, соответствующей динамическому углу крена, т.е. площади АВСD. Равенство этих площадей говорит о том, что судно под действием динамического кренящего момента
и перпендикуляром восстановленном из точки, соответствующей динамическому углу крена, т.е. площади АВСD. Равенство этих площадей говорит о том, что судно под действием динамического кренящего момента 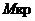 накренится до угла динамического крена
накренится до угла динамического крена 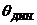 Малейшее превышение динамического кренящего момента
Малейшее превышение динамического кренящего момента 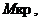 показанного на Рис. 3.15 приведет к опрокидыванию судна, так как для площади под графиком кренящего момента
показанного на Рис. 3.15 приведет к опрокидыванию судна, так как для площади под графиком кренящего момента  уже не найдется равной по величине площади под графиком ДСО.
уже не найдется равной по величине площади под графиком ДСО.
Как видно, решение задачи по нахождению опрокидывающего момента с помощью ДСО, сопряжено с необходимостью вычисления площадей и большим объемом вычислений. Для облегчения процедуры вычислений используется диаграмма динамической остойчивости (ДДО).
ДДО представляет собой графическую зависимость работы восстанавливающего момента от угла крена.
Такую диаграмму целесообразно построить заранее, сразу после построения ДСО, и использовать при решении динамических задач.
ДДО вычисляется на основе формулы (3.11), следовательно, график ДДО обладает свойствами интегральной кривой по отношению к графику подынтегральной функции, т.е. к ДСО. При углах крена θ = 0 и θ = θ3, где Мв = 0, ДДО должна иметь экстремальные точки, т.е. минимум и максимум, соответственно, а при угле крена θ = θm, где Мв(θ) принимает максимальное значение – ДДО будет иметь точку перегиба. Важно отметить, что ДДО при всех вариантах остойчивости судна (при всех h0) должна в начале координат иметь горизонтальную касательную.
Из прочих свойств ДДО можно отметить следующие:
- чем больше значение начальной метацентрической высоты hиспр, тем выше проходит ДДО, (т.к. ДСО также проходит выше и имеет большую площадь),
- так же будет возрастать угол заката, поскольку у соответствующих ДСО он увеличивается с ростом исходной метацентрической высоты (h0испр), (см. Рис.15).
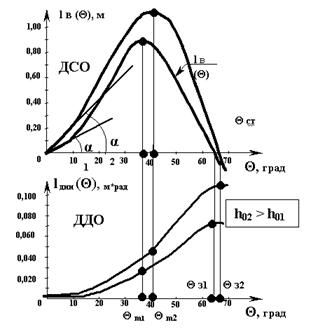 |
Рис. 15. Диаграммы статической и динамической остойчивости.
ДДО имеет две разновидности (как и соответствующие им ДСО):
- в виде графика работы Ав (θ) или
- в виде работы, отнесенной к водоизмещению судна lдин(θ):
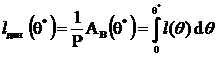 (3.12)
(3.12)
Величину lдин(θ) называют, по аналогии, плечом динамической остойчивости, хотя искать ему геометрическую интерпретацию не следует – эта величина получена чисто формальным путем. Размерность lдин – [м · рад].
Однако, учитывая независимость lдин от веса Р (и размеров) судна, возможно использовать её в задачах нормирования остойчивости, где удобно назначать универсальные константы-нормативы, которые могут использоваться на судах различного водоизмещения.