Особенности технических теорий ползучести
Существует два подхода к объяснению явления ползучести – физический и механический (феноменологический), и, соответственно, два типа теорий ползучести – физические и механические (технические). Задача механических теорий ползучести состоит в том, чтобы связать измеряемые в эксперименте величины – напряжения, деформации, скорости деформаций, температуру и время с помощью некоторого уравнения (или системы уравнений), носящего универсальный характер и называемого реологической функцией материала.
При построении теории ползучести не следует стремиться к универсальности, поскольку различного рода обобщения влекут за собой математические трудности при решении конкретных задач. Кроме того, при использовании сложных уравнений возникают сложности в определении различного рода коэффициентов и функций, входящих в эти уравнения, по имеющимся опытным данным. И, наконец, для ползучести характерен большой разброс опытных данных, и нет особого смысла рассматривать сложные уравнения, которые будут содержать приближенные (из-за этого разброса) исходные параметры.
Обычно информации, доставляемой испытаниями на чистую ползучесть, недостаточно для того, чтобы описать ползучесть при переменных нагрузках – в общем случае ползучести изменение деформаций сопровождается изменением напряжений. Для установки зависимостей между деформациями, напряжениями, скоростями их изменения и временем предварительно необходимо максимально ограничить число переменных и высказать предположение о том, между какими из них существует функциональная зависимость. Это предположение и носит название технической теории ползучести.
Итак, теория ползучести должна дать возможность на основе простейших испытаний материала определить его поведение в случае меняющихся во времени напряжений и деформаций, а также обеспечить определение закона изменения деформаций по заданному закону изменения напряжений и наоборот. В частном случае она должна позволить построить кривые релаксации по серии кривых ползучести. Очевидно, что при выборе теории ползучести лучшей теорией будет та, которая наиболее полно согласуется с данными экспериментов.
Как и в случае одномерной ползучести, основной вопрос, на который должна ответить теория ползучести – это вопрос о зависимости между координатами тензоров напряжений и деформаций (или скоростей деформаций). Различными исследователями были предложены варианты таких зависимостей, построенные на основе накопленных экспериментальных данных. Однако из-за скудности опытных данных, определяемой техническими трудностями проведения экспериментов принципиального характера, неизбежности разброса характеристик материала, а зачастую и из-за сложности полученных соотношений их применение н получило распространения. К тому же надежные эксперименты имеются только для плоского напряженного состояния, а для трехосного напряженного состояния имеется совсем мало сведений о закономерностях ползучести.
Вспомним, что примерно такое же положение существует и в теории пластичности, и, подобно теориям пластичности, теории ползучести при сложном напряженном состоянии в настоящее время строятся на основе гипотез, лишь частично подтверждаемых экспериментами. Очевидно, что в этом случае наиболее важен вопрос о том, какой именно принцип положен в основу теории, с чем связана переменность рассматриваемых величин во времени ( с сами временем, величиной накопленной деформации) и т.д. Различные формулировки уравнений, получаемых при этом, не слишком сильно разнятся, и при их выборе следует руководствоваться, в первую очередь, соображениями простоты и удобства.
При решении задач ползучести в условиях сложного напряженного состояния различают, как и для одноосного растяжения, установившуюся и неустановившуюся ползучесть. Обобщая понятие установившейся ползучести при одноосном растяжении на случай сложного напряженного состояния, можно утверждать, что это такой процесс деформирования материала во времени, интенсивность скоростей деформации остается неизменной. В случае однозначной зависимости между интенсивностью скоростей деформации и интенсивностью напряжений последняя также должна оставаться неизменной в процессе установившейся ползучести. Отметим, что хотя постоянство интенсивности не означает постоянства всех компонентов тензора напряжений, обычно для простоты расчетов полагаем, что в условиях установившейся ползучести все напряжения не меняются во времени.
Установившаяся ползучесть всегда имеет место в случае статически определимых задач при постоянстве во времени внешних сил. Действительно, в таких задачах напряжения определяются только уравнениями статики, а поскольку внешние силы постоянны, напряжения также не меняются во времени.
В статически неопределимых задачах для вычисления напряжений необходимо дополнительно привлекать уравнения Коши, куда входят деформации, которые изменяются во времени. В этих задачах даже при постоянных во времени внешних силах изменение деформаций будет приводить к изменению напряжений и их перераспределению по объему тела. Как показывают исследования неустановившейся ползучести, напряжения, изменяясь во времени, приближаются к значениям, получаемым из решения задачи установившейся ползучести, и в этом плане распределение напряжений при установившейся ползучести является как бы предельным.
Можно считать, что по прошествии некоторого промежутка времени наступает состояние ползучести, близкое к установившемуся. Если этот промежуток мал по сравнению с длительностью «жизненного цикла» рассматриваемого материала, то изучение ползучести можно проводить, основываясь на уравнениях установившейся ползучести, что значительно проще. В качестве критерия приближения к состоянию установившейся ползучести обычно принимают заметное превышение деформаций ползучести над упругими деформациями. В технических задачах это условие обычно выполняется. По этой причине, а также вследствие упомянутой простоты решения задач установившейся ползучести, в технике большей частью ограничиваются анализом установившейся ползучести.
Экспериментальные данные по установившейся ползучести могут быть обобщены в виде гипотез аналогично тому, как это было сделано в теориях пластичности, поскольку деформации ползучести также являются необратимыми. Обычно материал принимают изотропным и считают, что изменения объема при ползучести не происходит
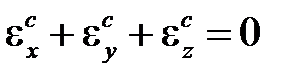 .
.
Как и в ассоциированном законе пластического течения, направляющие девиаторы напряжений и скорости ползучести считают совпадающими
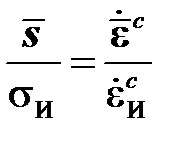 ,
,
что обычно наблюдается в испытаниях на чистую ползучесть.
Теория старения
Если уравнение семейства кривых ползучести при данной температуре записано в виде
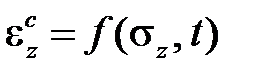 , (2.1.1)
, (2.1.1)
то самое простое предположение состоит в том, чтобыпридать этому соотношению универсальный характер, то есть считать его справедливым не только для ползучести при постоянномнапряжении, но и при переменном во времени. Этовыражение и определяет теорию старения в случае одномерной задачи.Уравнение (2.1.1) по форме и по существу не являетсяуравнением ползучести.Это закон нелинейной упругости материала, у которого упругие свойства меняются со временем, поскольку разгрузка в любой момент времени приводит к исчезновению неупругой деформации.
Удобство теории старения заключается в ее крайней простоте.При использовании этой теории нет необходимости задаватьсякаким-либо аналитическим выражением для функции 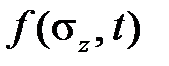 – можно пользоваться непосредственно кривымиползучести, построенными в обычных координатахдеформация – время при постоянных уровнях напряжений
– можно пользоваться непосредственно кривымиползучести, построенными в обычных координатахдеформация – время при постоянных уровнях напряжений
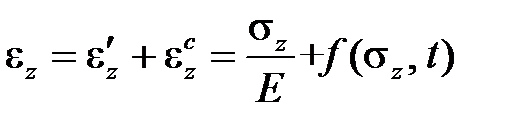 ,
, 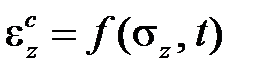 .
.
В расчетах теорию старения обычно используют в виде
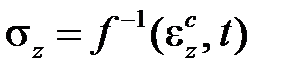 , (2.1.2)
, (2.1.2)
что при фиксированных значениях времени определяет изохронные кривые деформирования в обычных координатах 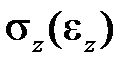 (рис.2.1.1б). Их получаются в результате обработки серии кривых чистой ползучести
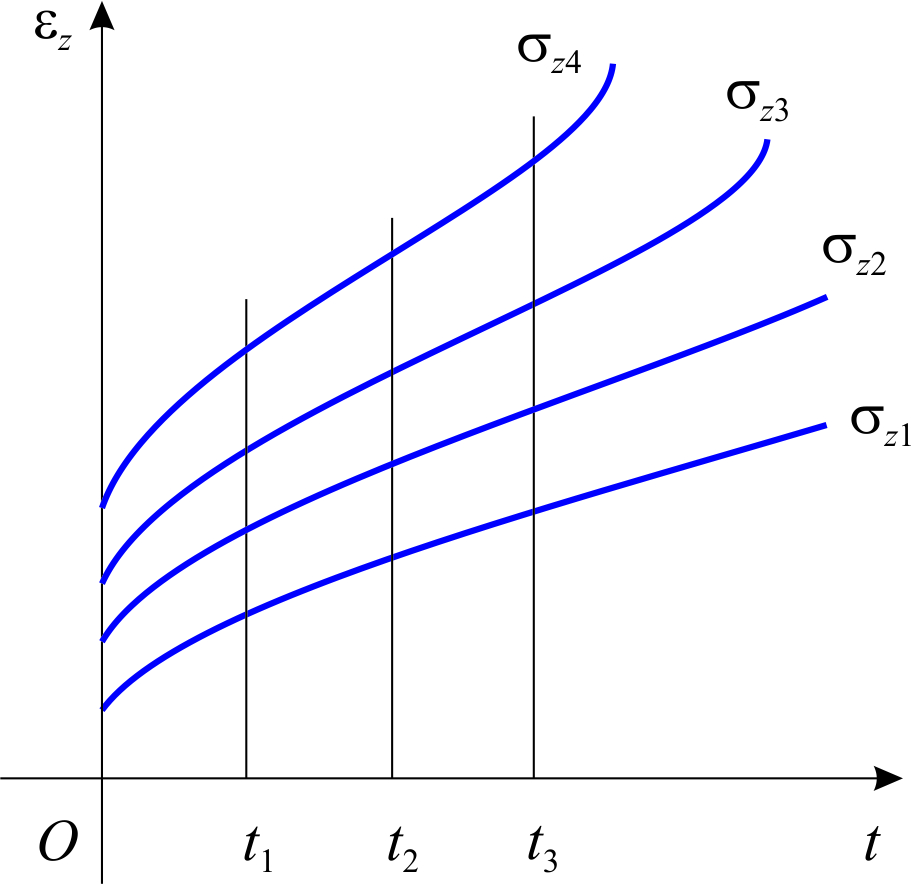
(рис.2.1.1б). Их получаются в результате обработки серии кривых чистой ползучести 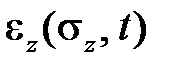 (рис.2.1.1а), связывая между собой деформации и напряжения при ряде последовательных фиксированных значений времени выдержки (рис.2.1.1).
(рис.2.1.1а), связывая между собой деформации и напряжения при ряде последовательных фиксированных значений времени выдержки (рис.2.1.1).
Модель подобного материала можно представить следующим образом: образец находится в агрессивной среде, которая разъедаетматериал, что приводит к уменьшению площади поперечного сечения, и упругая деформация увеличивается при постоянной нагрузке. Внешне этот процесс похож на процесс ползучести, нона самом деле деформация ползучести необратимаи аналогия ползучести металла с поведением рассмотренной системы образец – агрессивная среда чисто внешняя.
 | 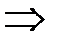 |  |
| а) | б) | |
| Рис.2.1.1 |
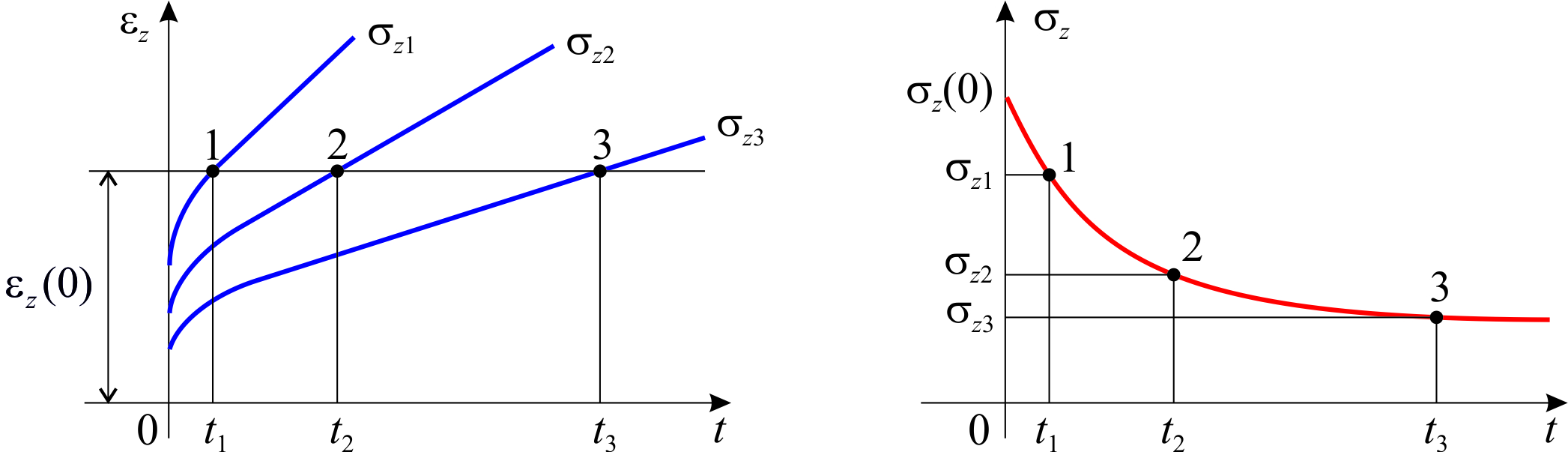
Рассмотрим метод построения кривой релаксации при одноосном растяжении по серии кривых ползучести на основе теориистарения. Предположим, что кривые ползучести при различных напряжениях известны (рис.2.1.2а). Допустим, что необходимо построить кривую релаксации при начальном напряжении 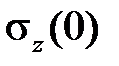 . В таком случае надо на кривых ползучести для различных значений напряжения провести горизонтальную прямую на расстоянии
. В таком случае надо на кривых ползучести для различных значений напряжения провести горизонтальную прямую на расстоянии 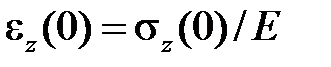 от оси абсцисс. Точки пересечения этой прямой с графиками зависимости деформации от времени определяют величины напряжений для определенных значений времени. Полученные результаты легко перенести в координаты t,
от оси абсцисс. Точки пересечения этой прямой с графиками зависимости деформации от времени определяют величины напряжений для определенных значений времени. Полученные результаты легко перенести в координаты t, 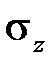 и построить кривую релаксации (рис.2.1.2б).
и построить кривую релаксации (рис.2.1.2б).
Впервые теория старения была предложена Содербергом, а ее обобщение и анализ были даны Ю.Н. Работновым. В случае неоднородного напряженно деформированного состояния определяющее уравнение теории старения записывают в интенсивностях
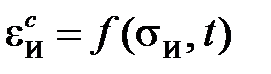 или
или 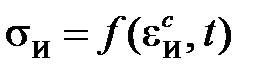 . (2.1.3)
. (2.1.3)
Определение напряжений и деформаций для некоторого значения времени по теории старения эквивалентнорешению задачи по деформационной теории для известной диаграммы деформирования. То есть, если при расчете какой-либо детали на ползучесть необходимо определить напряжения и деформации для заданного значения времени, то следует провести расчет на прочность и жесткость этой детали, используя изохронную кривую деформирования для принятого значения времени.
Если изохронные кривые деформирования подобны, то есть могут быть получены из одной кривой умножением ее ординат на некоторую величину, являющуюся функцией времени, то расчеты значительно упрощаются. В этом случае зависимость напряжения от деформации и времени может быть представлена в виде произведения двух функций, одна из которых 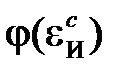 является только функцией деформаций, а вторая
является только функцией деформаций, а вторая 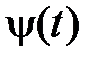 – только функцией времени
– только функцией времени
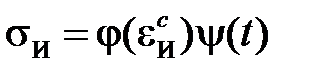 .
.
 | |
| а) | б) |
| Рис.2.1.2 |
Здесь надо иметь в виду, что подобие кривых ползучести еще не означает подобия изохронных кривых деформирования. Второе подобие является следствием первого только в том случае, если можно пренебречь упругими деформациями по сравнению с деформациями ползучести. Хорошее согласование с результатами эксперимента дает следующее представление функции 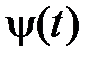
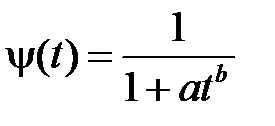 ,
,
где aи b – это константы материала, зависящие от температуры. В случае постоянной деформации это выражение описывает релаксацию напряжений.
Строго говоря, теория старения не может описывать ступенчатое нагружение, так как в момент изменения напряжения деформация ползучести должна иметь разрыв, что, очевидно, невозможно. Тем не менее, на практике теорию старения применяют, но только в тех случаях, когданапряжение с течением времени изменяется плавно, без резких измененийнапряженного состояния.
Теория течения
Дифференцирование кривых ползучести по времени приводит к выражению
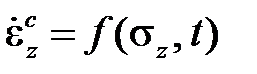 , (2.2.1)
, (2.2.1)
которое и является определяющим соотношением теории теченияв случае одномерной задачи. Она, таким образом, постулирует наличие связи между напряжением, скоростью деформации ползучести и временем. Эта теория была предложена Девенпортом и получила довольно широкое распространение в связи с работами Л.М. Качанова. В случае неоднородного напряженно деформированного состоянияреологическую функцию записывают в интенсивностях
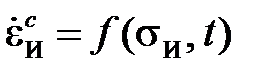 .
.
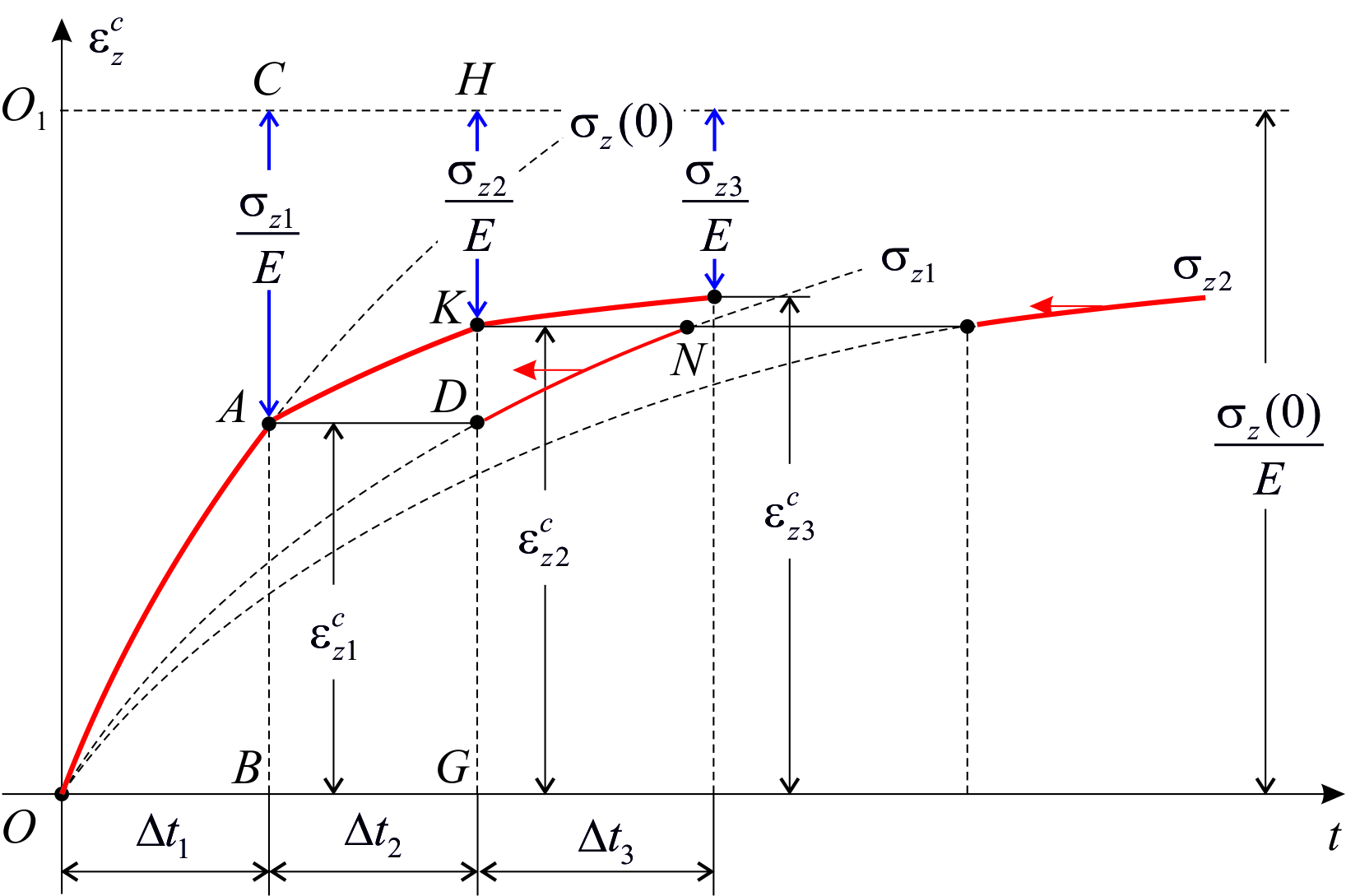
Рассмотрим метод построения кривой релаксации при одноосном растяжении по серии кривых ползучести на основе этой теории. Допустим, что необходимо построить кривую релаксации при начальном напряжении 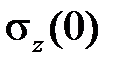 . Предположим, что кривые ползучести для различных величин напряжений известны (рис.2.2.1). Проведем на расстоянии
. Предположим, что кривые ползучести для различных величин напряжений известны (рис.2.2.1). Проведем на расстоянии 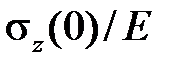 от оси абсцисс горизонтальную прямуюO1CH(при этом учитываем, что в начальный момент времени деформация ползучести еще не успела накопиться). Разобьем промежуток времени на ряд небольших интервалов Δt. Полагаем, что за время Δt1, считая от начального момента, процесс нарастания деформации ползучести протекает при постоянном напряжении
от оси абсцисс горизонтальную прямуюO1CH(при этом учитываем, что в начальный момент времени деформация ползучести еще не успела накопиться). Разобьем промежуток времени на ряд небольших интервалов Δt. Полагаем, что за время Δt1, считая от начального момента, процесс нарастания деформации ползучести протекает при постоянном напряжении 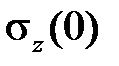 , тогда увеличение деформации ползучести
, тогда увеличение деформации ползучести 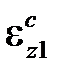 равно длине отрезка AB. Учитывая, что полная деформация в процессе релаксации не меняется и равна начальному значению
равно длине отрезка AB. Учитывая, что полная деформация в процессе релаксации не меняется и равна начальному значению
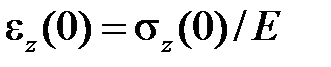 ,
,
можно определить величину упругой деформации для значения времени t1 = Δt1
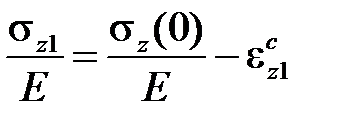 .
.
Эта величина в выбранном масштабе выражается отрезком AC.
Во второй промежуток времени Δt2 можно приближенно считать, что процесс нарастания деформации протекает при постоянном напряжении 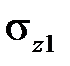 . Согласно теории течения, скорость деформации ползучести является функцией напряжения и времени, а от величины деформации ползучести она не зависит. Поэтому начальная скорость деформации ползучести на промежутке времени Δt2 определяется тангенсом угла наклона касательной в точке D к кривой ползучести при напряжении
. Согласно теории течения, скорость деформации ползучести является функцией напряжения и времени, а от величины деформации ползучести она не зависит. Поэтому начальная скорость деформации ползучести на промежутке времени Δt2 определяется тангенсом угла наклона касательной в точке D к кривой ползучести при напряжении 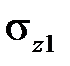 . Следовательно, на промежутке времени Δt2 деформация ползучести нарастает по закону, изображенному линией AK, представляющей часть кривой ползучести DNпри напряжении
. Следовательно, на промежутке времени Δt2 деформация ползучести нарастает по закону, изображенному линией AK, представляющей часть кривой ползучести DNпри напряжении 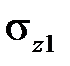 , передвинутой параллельно самой себе из точки Dв точку A.Деформация ползучести
, передвинутой параллельно самой себе из точки Dв точку A.Деформация ползучести 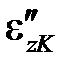 для значения времени t2выражается отрезком KG, а упругая – отрезком KH
для значения времени t2выражается отрезком KG, а упругая – отрезком KH
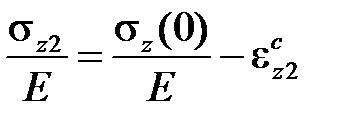 .
.
Умножением упругой деформации на модуль Юнга можно получить напряжения для соответствующих значений времени.
Неудобство изложенного метода построения кривой релаксации заключается в том, что для его использования необходимо располагать большим количеством кривых ползучести. Чтобы этого избежать, можно использовать какие-либо аппроксимации кривых ползучести.Это может быть, например, закон Нортона-Бейли, который в случае одномерной задачи и в общем случае напряженно-деформированного состояния записывают соответственно
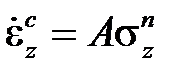 ,
, 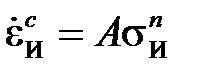 (2.2.2)
(2.2.2)
где n = f(T) и A = f(t, T) – это константы материала.
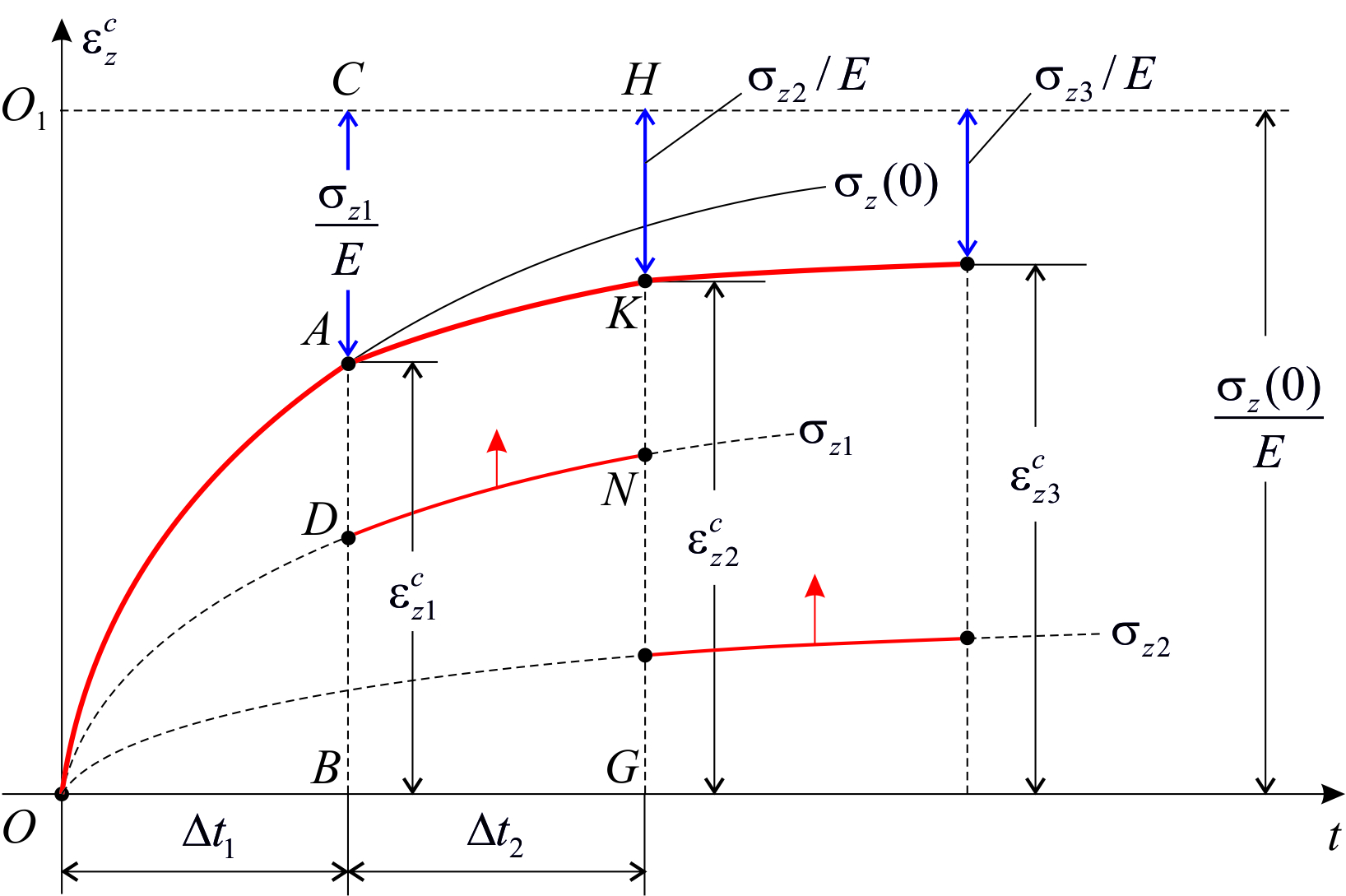 |
| Рис.2.2.1 |
Теория течения дает удовлетворительные результаты при слабо меняющихся напряжениях, даже лучше, чем теория старения, хотя явное введение временив определяющиеуравнения лишено механического смысла и приводит к противоречиям.В частности при нагружениях, отличающихся от чистой ползучести, возникает неразрешимая проблема: какой момент времени принять за начальный. Это может быть начало испытания или момент, когда напряжение стало достаточно большим, и т.д.
2.3. Теория упрочнения
Теория упрочнения основывается на предположении том, что изменение скорости ползучести в процессе выдержки связано не со временем, а с более вещественным параметром – накопленной деформацией ползучести
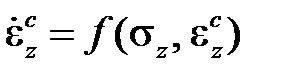 . (2.3.1)
. (2.3.1)
Информация для определения функции fостается прежней: после дифференцирования кривых чистой ползучести в выражениях(2.1.1) и (2.2.1) устраняют параметр t.В случае неоднородного напряженно деформированного состояния используют реологическую функцию
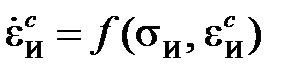 .
.
Эта теория первоначально была предложена Людвигом, Надаи и Девенпортом. Дальнейшее ее развитие принадлежит Ю.Н. Работнову.
Метод построения кривой релаксации по серии кривых ползучести аналогичен способу построения кривой релаксации по теории течения. Различие состоит лишь в том, что согласно теории упрочнения скорость деформации ползучести является функцией напряжения и деформации ползучести и от времени не зависит.Поэтому начальная скорость деформации ползучести на втором промежутке времени Δt2 определяется тангенсом угла наклона касательной в точке Dк кривой ползучести при напряжении 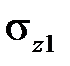 (рис.2.3.1),где точка D является точкой пересечения горизонтали, проведенной из точки A, с кривой ползучести при напряжении
(рис.2.3.1),где точка D является точкой пересечения горизонтали, проведенной из точки A, с кривой ползучести при напряжении 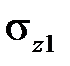 .Следовательно, согласно теории упрочнения на промежутке времени Δt2 пластическая деформация нарастает по закону, изображенному линией AK.А эта линия представляет собой участок кривой ползучести при напряжении
.Следовательно, согласно теории упрочнения на промежутке времени Δt2 пластическая деформация нарастает по закону, изображенному линией AK.А эта линия представляет собой участок кривой ползучести при напряжении 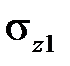 , передвинутый параллельно самому себе из точки D в точкуA. Далее за промежуток времени Δt3 рассуждения участок кривой строится с использованием те же рассуждения.
, передвинутый параллельно самому себе из точки D в точкуA. Далее за промежуток времени Δt3 рассуждения участок кривой строится с использованием те же рассуждения.
 |
| Рис.2.3.1 |
Ввиду того, что скорость деформации ползучести для некоторого значения времени по теории упрочнения меньше, чем по теории течения, кривая релаксации, построенная на ее основе, располагается всегда выше кривой релаксации, построенной по теории течения.Теория упрочнения лучше других описывает ползучесть при переменном напряжении, если последнее не меняет знак. Однако сопоставление с экспериментальными кривыми ползучести при ступенчатом нагружении свидетельствует о довольно существенных их различиях:
а) при уменьшающемся напряжении 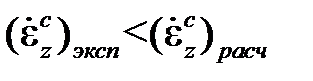 ;
;
б) при ступенчатом увеличении напряжения наоборот 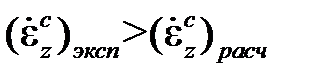 .
.
Теория идеальной вязкости
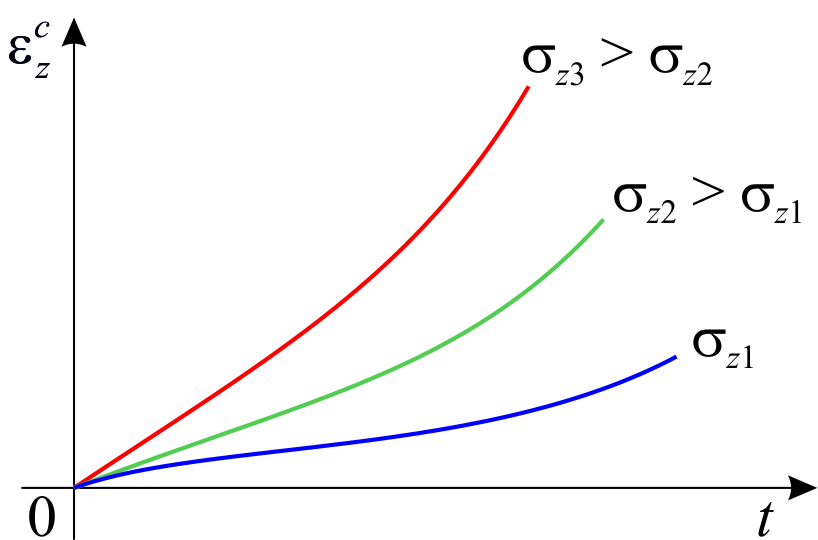
Предположим, что приползучести образца отсутствует первая стадия (или ей можнопренебречь в силу малости) и кривые ползучести имеют вид,представленный на рис.2.4.1. Для такой серии кривых ползучестисправедлива аппроксимация вида
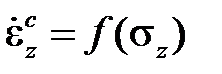 . (2.4.1)
. (2.4.1)
Это выражениеи определяет теорию идеальной вязкости в случаеодномерной задачи. Реологическую функцию 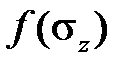 обычно принимают в виде зависимости скорости установившейся ползучести (стадия II)от напряжения с использованием степенной функции (закон Нортона-Бейли)
обычно принимают в виде зависимости скорости установившейся ползучести (стадия II)от напряжения с использованием степенной функции (закон Нортона-Бейли)
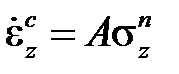
или экспоненциальной
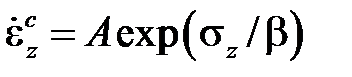 ,
,
где A, nи β – это характеристики материала при данной температуре. Для определения скорости полной деформации необходимо еще учесть упругуюдеформацию,которая подчиняется закону Гука
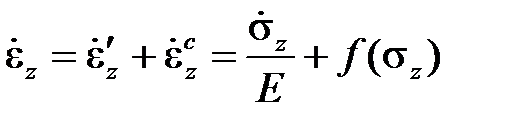 .
.
В теории идеальной вязкости соотношению (2.4.1) придается универсальный характер, то есть предполагается, что оно справедливо не только при монотонном, но и при переменном нагружении. Применимость этой теории определяется тем, в какой мере кривые ползучести в координатах деформация ползучести– время можно аппроксимировать прямыми линиями.
Анализ существующих экспериментальныхданных показывает, что это оказывается возможным в двух крайних случаях:
1) в случае, когда речь идет о весьма значительныхсроках службы изделия и основную часть времени процесс ползучести протекает с постоянной скоростью;
2) в случае кратковременной ползучести, то есть ползучести при очень высокой температуре и высоком уровне напряжений.
 |  |
| Рис.2.4.1 | Рис.2.4.2 |
Здесь типичная картина – это практически полное отсутствие первой стадии и не ярко выраженный характер третьей стадии ползучести (рис.2.4.1), причемразрушение образца происходит за относительно малое время (отнескольких секунд до нескольких часов).
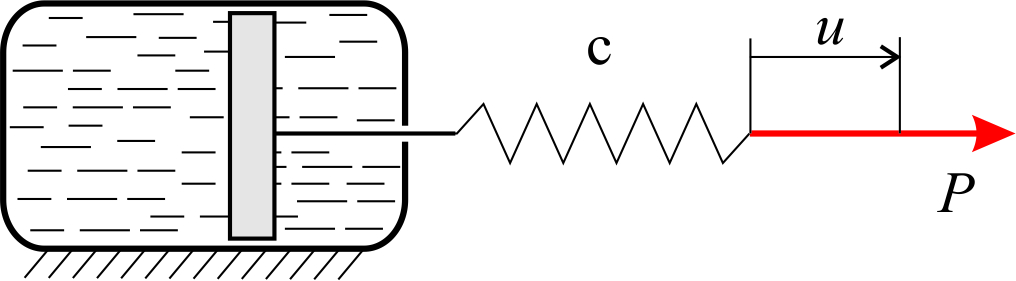
Как и для идеально пластичного, для идеально вязкого материала также существует простая механическая модель (рис.2.4.2), где сухое трение заменено жидкостным (модель Максвелла).Жидкость в демпфере сопротивляется перемещению поршня внутри него с силой, зависящей от скорости последнего, при этом полагаем, что эта зависимость нелинейна и отражается функцией 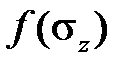 в выражении(2.4.1). Смещение поршня представляет аналог неупругой деформации
в выражении(2.4.1). Смещение поршня представляет аналог неупругой деформации 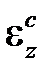 . В отличие от идеально пластического тела здесь нагружение может быть как кинематическим, так и силовым.
. В отличие от идеально пластического тела здесь нагружение может быть как кинематическим, так и силовым.
Метод построения кривой релаксации с помощью теории идеальной вязкости очень прост – скорость деформации ползучести не зависит от времени (она при установившейся ползучестисчитается постоянной), поэтому на каждом новом этапе приращения времени скорость деформации ползучести определяется только напряжением (рис.2.4.3).
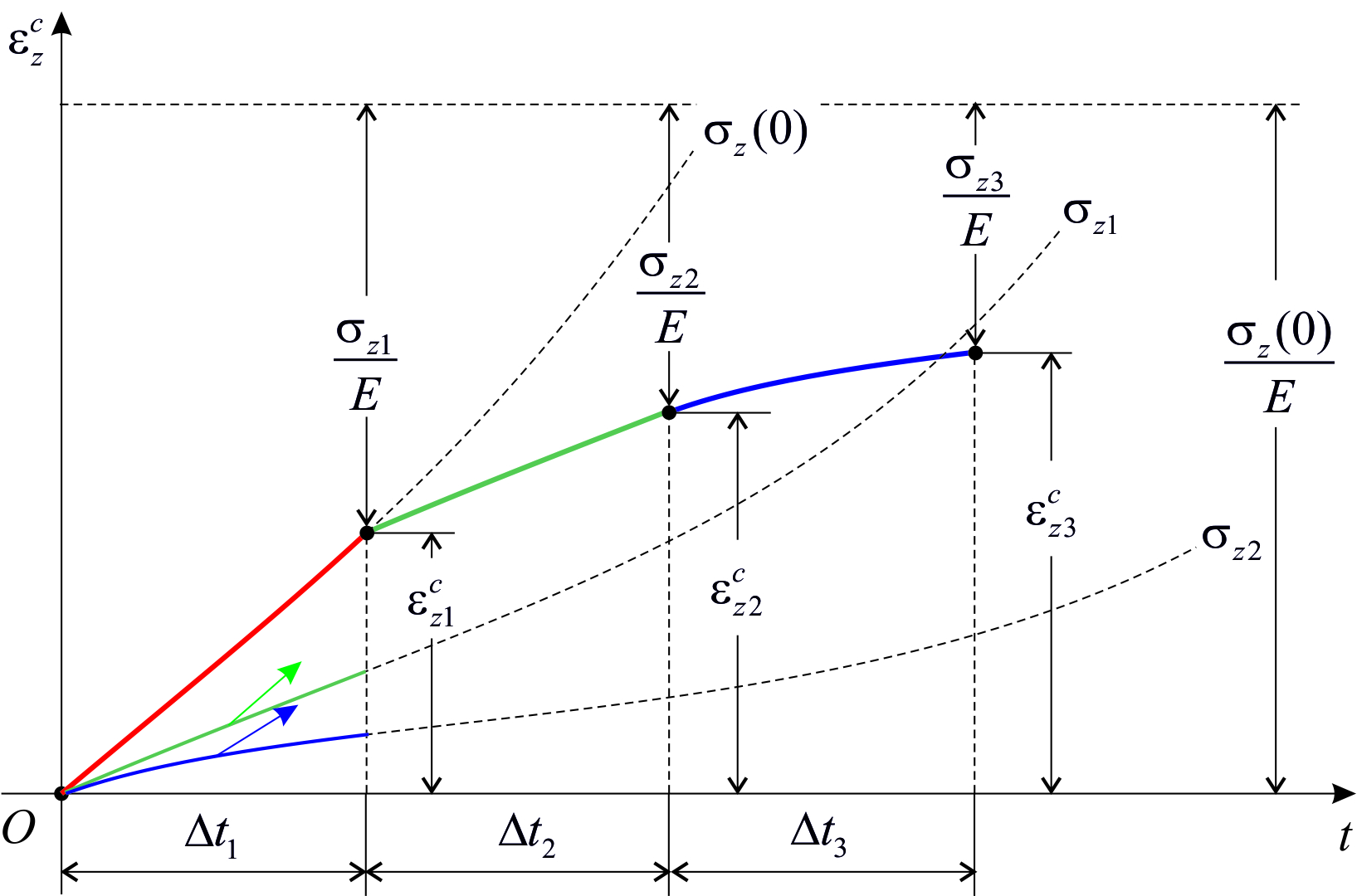 |
| Рис.2.4.3 |
В случае сложного напряженно-деформированного состояниятеориюидеальной вязкостив неизотермических задачахформулируют в тензорной (векторной) форме: чем выше напряжение, тем выше скорость установившейся ползучести
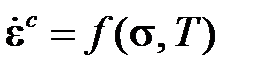 .
.
Направляющие девиаторы напряжений и скорости ползучести 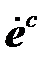 совпадают
совпадают
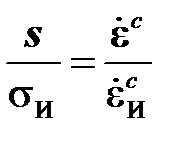 ,
,
что обычно наблюдается в испытаниях на чистую ползучесть. Реологическая функция имеет вид
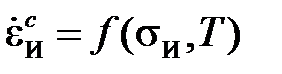 .
.
С учетом этого получают следующие определяющее выражениетеории идеальной вязкости
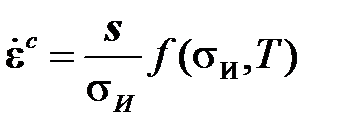 .
.
Как и в одномерном случае, здесь для простоты пренебрегают первой стадией и третьей стадиейползучести и считают, что скорость ползучестине зависит от длительности выдержки, а только от напряжения и температуры, которая поддерживается постоянной в процессе ползучести.
 |  |
| а) | б) |
| Рис.2.4.4 |
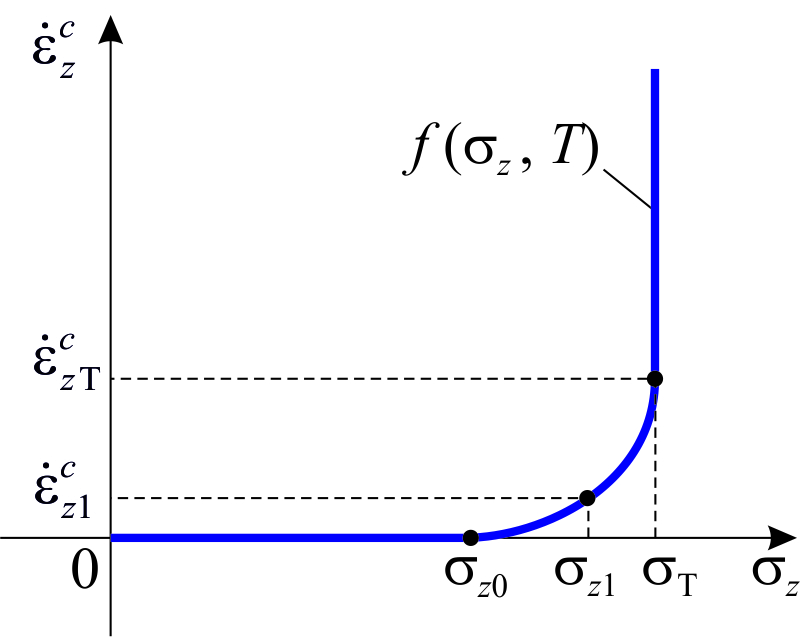
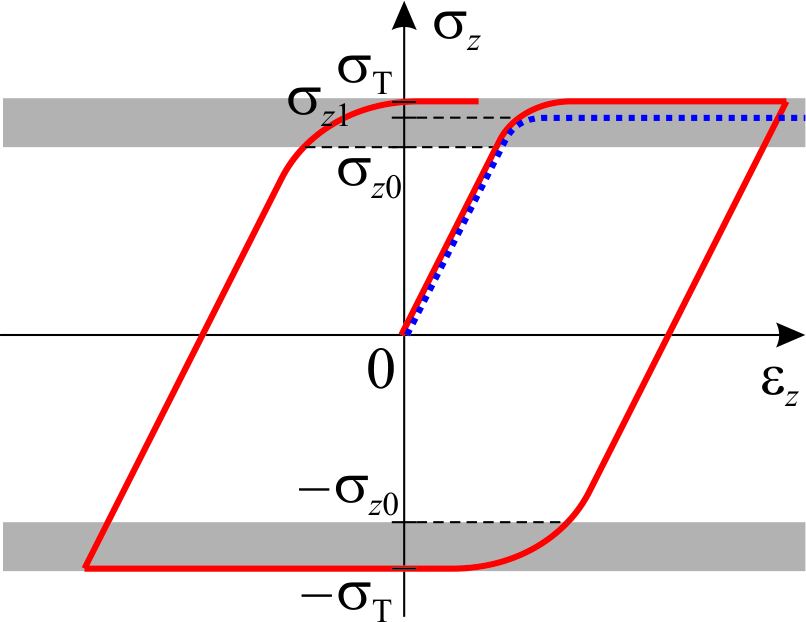
Хотя идеально пластичныйматериал принципиально отличается от идеально вязкого (различие междусклерономностью и реономностью), однако можно показать, что он представляет предельный случай идеально вязкого. Представим себе, что идеально вязкое тело характеризуется функцией 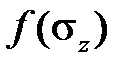 , график которой показан на рис.2.4.4а: при sz< sz0 скорость ползучести равна нулю, при sz = sT скорость
, график которой показан на рис.2.4.4а: при sz< sz0 скорость ползучести равна нулю, при sz = sT скорость 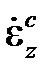 – произвольная величина (больше некоторого значения
– произвольная величина (больше некоторого значения 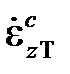 ). Тогда в координатах {sz,ez} поведение материала отражается схемой, показанной на рис.2.4.4б:
). Тогда в координатах {sz,ez} поведение материала отражается схемой, показанной на рис.2.4.4б:
1. затемненные области здесь – это те области, где может происходить неупругое деформирование;
2. при напряженииsz < sz0 деформирование является упругим;
3. при деформировании со скоростью, превышающей 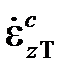 , диаграмма деформирования выходит на напряжение sT и далее скорость неупругого деформирования оказывается равна
, диаграмма деформирования выходит на напряжение sT и далее скорость неупругого деформирования оказывается равна 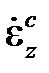 (при этом, естественно, скорость изменения напряжений равна нулю);
(при этом, естественно, скорость изменения напряжений равна нулю);
4. если скорость 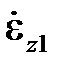 положительна, но меньше
положительна, но меньше 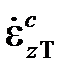 , то максимальное напряжение – это такое напряжение, при котором скорость ползучести равна
, то максимальное напряжение – это такое напряжение, при котором скорость ползучести равна 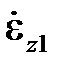 , то есть оно меньше sT (пунктирная линия на рис.2.4.4б).
, то есть оно меньше sT (пунктирная линия на рис.2.4.4б).
Ползучесть и релаксация возможны лишь пока точка состояния {sz,ez} лежит в затемненных областях.
Сужая диапазон (sT – s0), мы одновременно сужаем затемненный коридор, где происходит неупругое деформирование; при этом материал, оставаясь реономным, все меньше отличается от идеально пластического. Таким образом, отличие между склерономностью и реономностью не столь антагонистично, как кажется на первый взгляд. Добавим, что это относится не только к рассмотренным идеальным моделям.
