Понятие знакопеременного ряда.

Числовой ряд

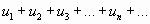
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.

,

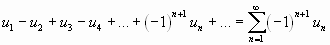где 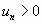для всех 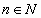(т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно). Например,

;

;

.

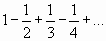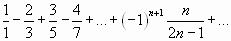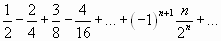Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714г. Лейбницем в письме к И.Бернулли).

Признак Лейбница. Абсолютная и условная сходимость ряда.

Теорема (Признак Лейбница).

Знакочередующийся ряд сходится, если:

Последовательность абсолютных величин членов ряда монотонно убывает, т.е. ;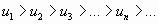

Общий член ряда стремится к нулю: .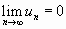

При этом сумма S ряда удовлетворяет неравенствам

.

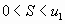Замечания.

Исследование знакочередующегося ряда вида

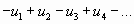
(с отрицательным первым членом) сводится путем умножения всех его членов на 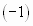к исследованию ряда .

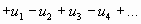Ряды, для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).

Соотношение 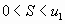позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой .

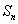Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд 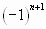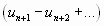, сумма которого по модулю меньше первого члена этого ряда, т.е. 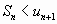. Поэтому ошибка меньше модуля первого из отброшенных членов.

Пример. Вычислить приблизительно сумму ряда .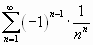

Решение: данный ряд Лейбницевского типа. Он сходится. Можно записать:

.

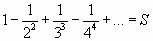Взяв пять членов, т.е. заменив 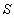на

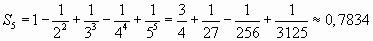, сделаем ошибку, меньшую,

чем 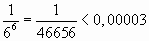. Итак, .

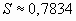Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

.

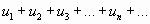Если сходится ряд

,

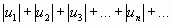составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Признак сходимости Лейбница для знакочередующихся рядов служит достаточным признаком сходимости знакочередующихся рядов.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся.

Упражнения.

Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

;

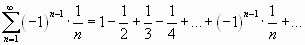Решение.

Члены данного ряда по абсолютной величине монотонно убывают:

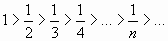и

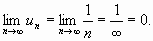
Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.

Ряд 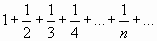, составленный из абсолютных величин данного ряда, является гармоническим рядом, который, расходится. Поэтому данный ряд сходится условно.

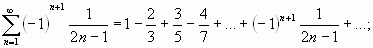
Решение.

Члены данного ряда по абсолютной величине монотонно убывают:

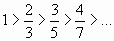, но

.

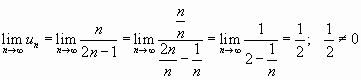Ряд расходится, так как признак Лейбница не выполняется.

;

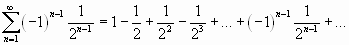Решение.

Используя признак Лейбница, получим

; ,

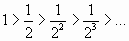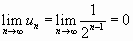т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

.

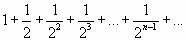Это геометрический ряд вида 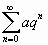, где 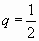, который сходится. Поэтому данный ряд сходится абсолютно.

;

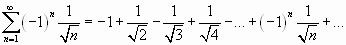Решение.

Используя признак Лейбница, имеем

;

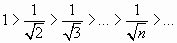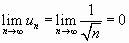, т.е. ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

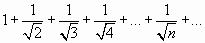, или

.

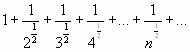Это обобщенный гармонический ряд, который расходится, так как 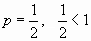. Следовательно, данный ряд сходится условно.

III. Функциональный ряд