Решениетригонометрическихнеравенств
1)а)sin2x> 0б)sin(x + п/4) 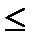 0в)cos
0в)cos 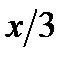 > 0г)сosx
> 0г)сosx  1д)tg(3x – 2) < -
1д)tg(3x – 2) < - 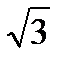
Ответ:а) 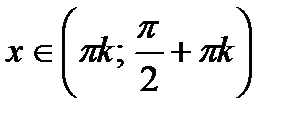 ; б)
; б) 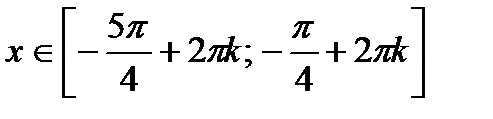 ;в)
;в) 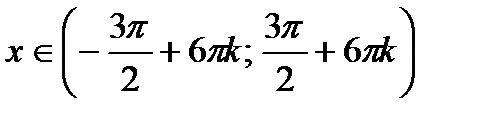 г)
г) 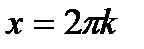 ;д)
;д) 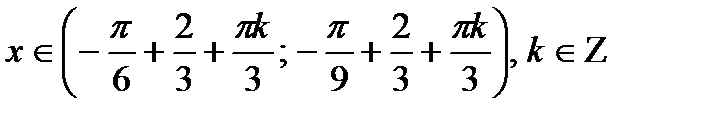
2) 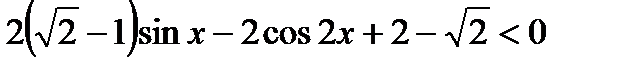
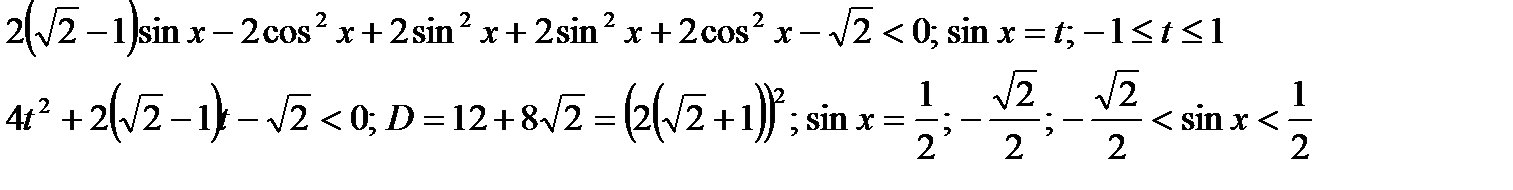
Ответ:x 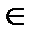 (- п/4 + 2пк;п/6 + 2пк)
(- п/4 + 2пк;п/6 + 2пк)  (5п/6 + 2пк;5п/4 + 2пк), k
(5п/6 + 2пк;5п/4 + 2пк), k 
3)cos3x sin3x + cos3x sin 3x < 3/8
cos3x (3sinx – 4sin3x) + (4cos 3x –3cosx)sin 3x = 3cos 3x sinx - 3 cosx sin 3x = 3cos x sinx 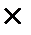
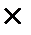 (cos2x – sin2x) = 3/4 sin4x; sin4x < 1/2;4x
(cos2x – sin2x) = 3/4 sin4x; sin4x < 1/2;4x 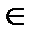 (5п/6 + 2пк;13п/6 + 2пк)
(5п/6 + 2пк;13п/6 + 2пк)
Ответ: x 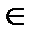 (5п/24 + пк/2;13п/24 + пк/2), k
(5п/24 + пк/2;13п/24 + пк/2), k 
4)8sin6x – cos6x > 0
1 способ)(2sin2x)3 – (cos2x)3 = (2 – 3cos2x)(3cos4x – 6cos2x + 4);cos2x = t;
(2 – 3t)(3t4 – 6t2 + 4) > 0; ( Д< 0 ) ; cos2x < 2/3; 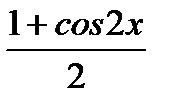 <2/3; cos2x <1/3
<2/3; cos2x <1/3
Ответ:x 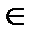 (1/2 arccos 1/3 + пk; п - 1/2arccos 1/3 + пk), k
(1/2 arccos 1/3 + пk; п - 1/2arccos 1/3 + пk), k 
2 способ)а)cosx = 0; 8sin6x> 0; sinx  0; x = п/2 + пk – решениенеравенства
0; x = п/2 + пk – решениенеравенства
б)cosx  0; 8tg6x> 1;
0; 8tg6x> 1; 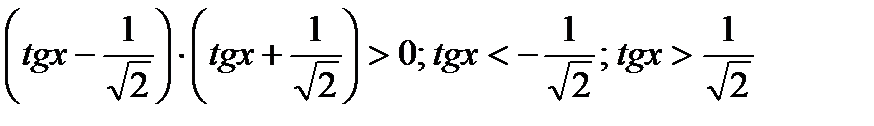
Ответ:x 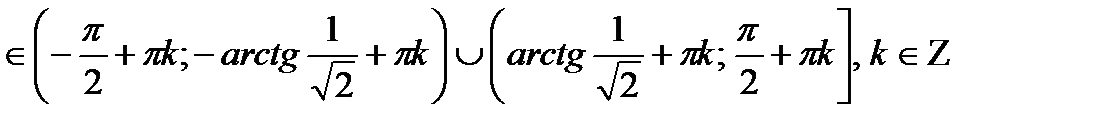
5) 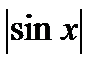 >cos2x
>cos2x
а)sinx  0;sinx > 1 – sin2x; D = 5; sinx >
0;sinx > 1 – sin2x; D = 5; sinx > 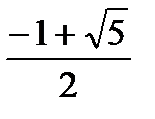 б)sinx < 0; sinx <
б)sinx < 0; sinx < 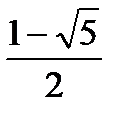
Ответ: x 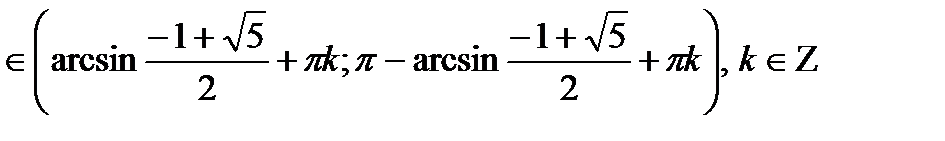
6) 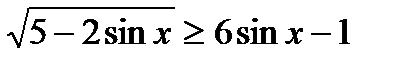
Cоответствует 2 сист.1) 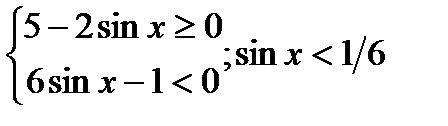 2)
2) 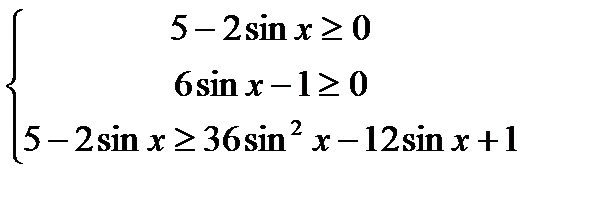
18sin2x – 5sinx – 2 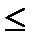 0; D = 132; sinx = 1/2; - 2/9; 1/6
0; D = 132; sinx = 1/2; - 2/9; 1/6 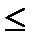 sinx
sinx 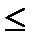 1/2;sinx
1/2;sinx 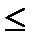 1/2;
1/2;
Ответ:x 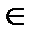 [5п/6 + 2пк;13п/6 + 2пк], k
[5п/6 + 2пк;13п/6 + 2пк], k 
7)1 – cosx<tgx - sinx;ОДЗ: x 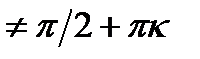
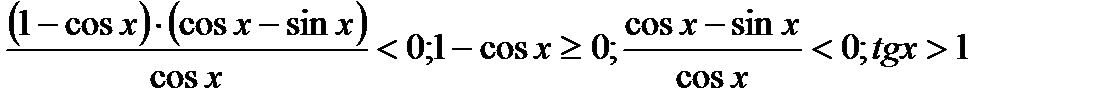 ; Отв: x
; Отв: x 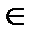 (п/4 + пк;п/2 + пк)
(п/4 + пк;п/2 + пк)
Hеравенства с обратными тригонометрическими функциями.
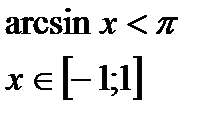 | 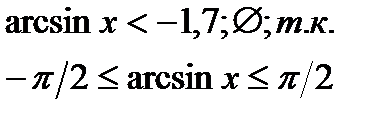 | 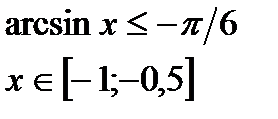 | 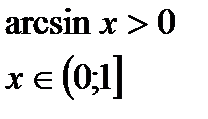 |
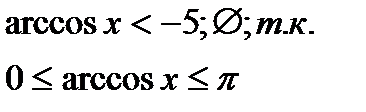 | 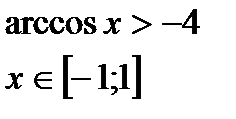 | 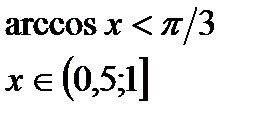 | 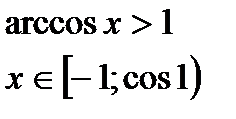 |
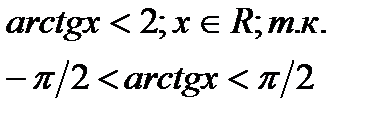 | 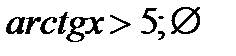 | 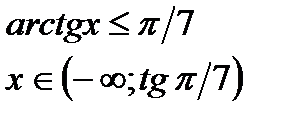 | 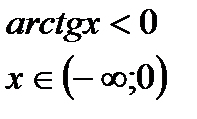 |
а) 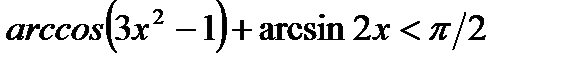
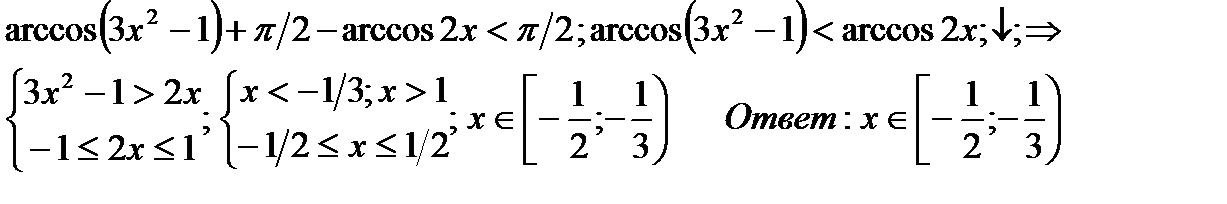
б)arcсos2x<arcos(1 – x)
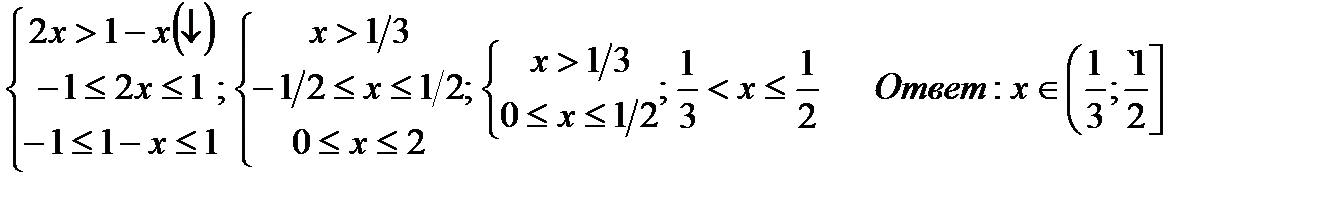
в-1) 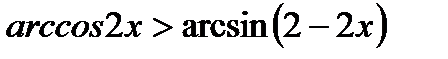
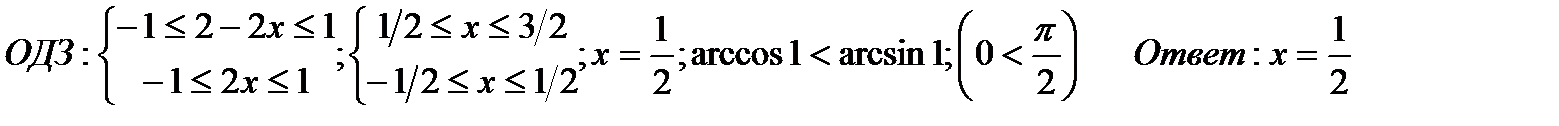
в-2) 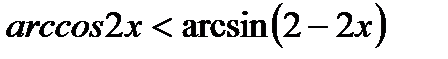
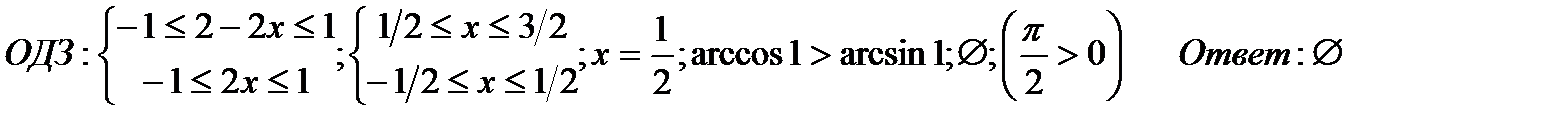
г) 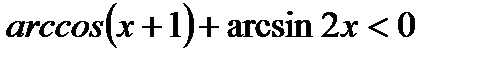
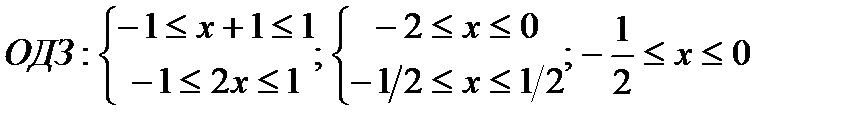
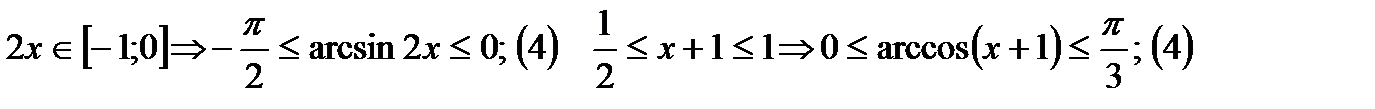
В 4четверти функции sinxи cosxвозрастают. Можно взять любую из них.
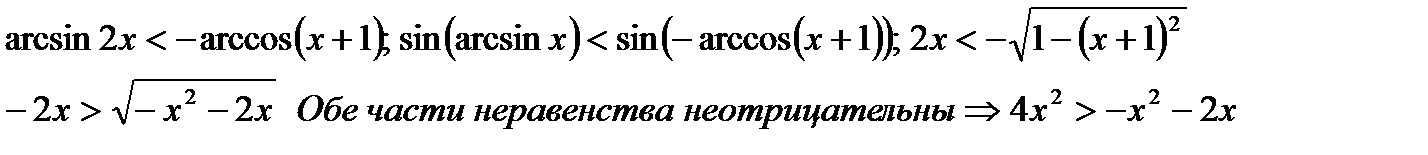
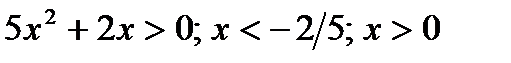 С учётом ОДЗ получим
С учётом ОДЗ получим 
д)Найти множество значений функции 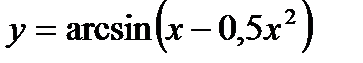
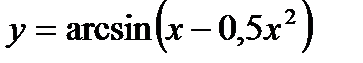 - парабола. Ветви направленывверх.
- парабола. Ветви направленывверх. 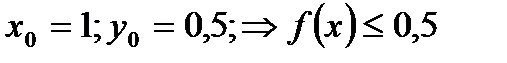 Рассматривается функция
Рассматривается функция 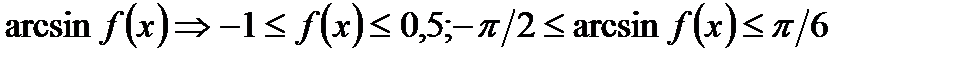
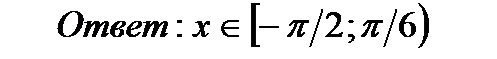
е)Найти множество значений функции 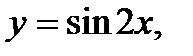 если
если 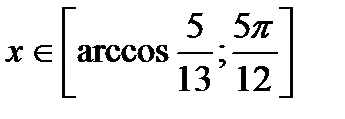
Удобно обозначить 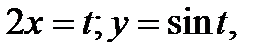 если
если 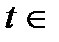
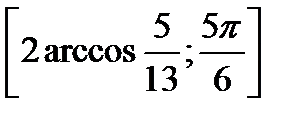
Самое близкое к 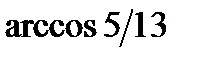 из известных значений 0,5.
из известных значений 0,5.
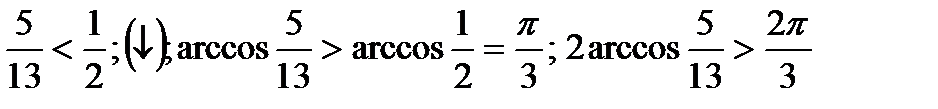
Так как функция 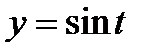 убывает на промежутке
убывает на промежутке 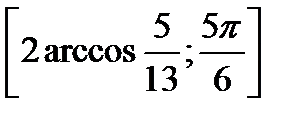 -2четверть, то наименьшее значение она будет принимать в начале промежутка, а наименьшее – в конце.
-2четверть, то наименьшее значение она будет принимать в начале промежутка, а наименьшее – в конце.
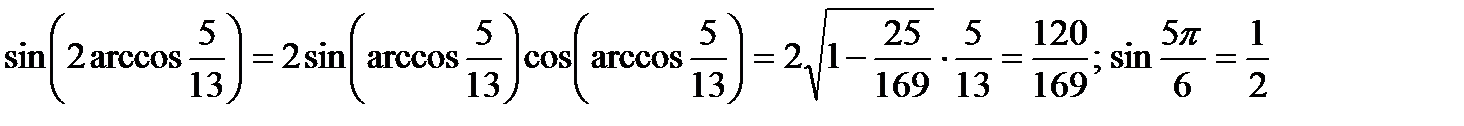
Так как функция непрерывная, то её множество значений 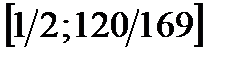
ж)Найти множество значений функции 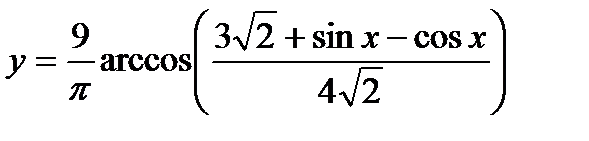
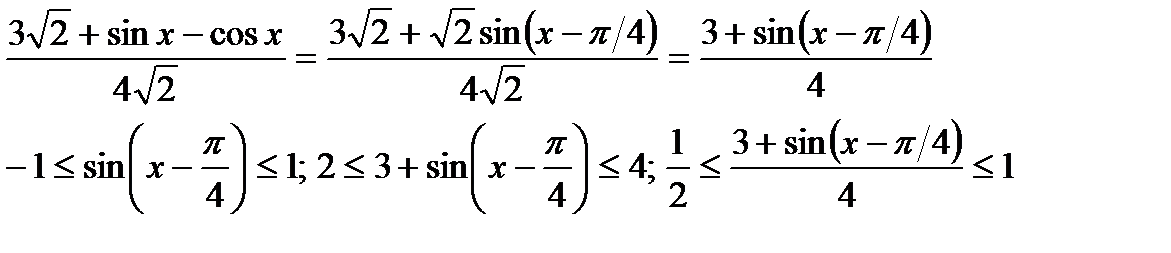
Так как функция 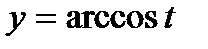 убывает, то возьмёмarccos от каждой части неравенства и поменяем знаки.
убывает, то возьмёмarccos от каждой части неравенства и поменяем знаки. 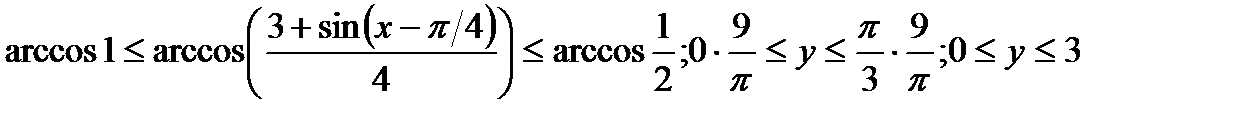
Так как функция непрерывная, то её множество значений 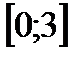
ЭКЗАМЕНАЦИОННАЯРАБОТА– ПАРАМЕТРЫ
1)Решитенеравенство
log 1/2(3x + 5)  log
log 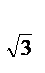 3log 1/3(2x - 7)
3log 1/3(2x - 7)  log
log 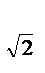 2
2
2)Решитеуравнение
sin2x - 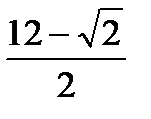 sinx - 3
sinx - 3 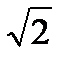 = 0cos2x -
= 0cos2x - 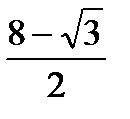 cosx - 2
cosx - 2 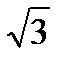 = 0
= 0
3)Решитеcистемууравнений
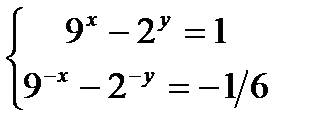
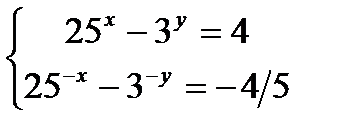 4)Решитенеравенство
4)Решитенеравенство
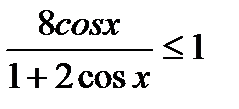
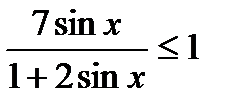
5*)Прикакихзначенияхруравнениенеимееткорней ?
cos2x – (р – 2)cosx + 4р + 1 = 0sin2x + (р + 2)sinx + 3р + 1 = 0
РЕШЕНИЕ1ВАРИАНТА.
1)log 1/2(3x + 5)  log
log 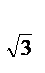 3ОДЗ: х > - 5/3
3ОДЗ: х > - 5/3
3x + 5 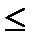 1/4; х
1/4; х 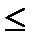 -
- 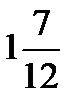 ;Ответ:x
;Ответ:x 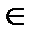 (-1
(-1 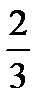 ; -
; - 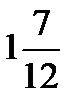 ]
]
2)sin2x - 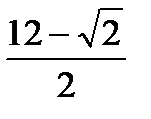 sinx - 3
sinx - 3 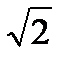 = 0
= 0
D = (6 + 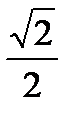 )2;sinx = 6; -
)2;sinx = 6; - 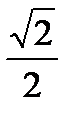 ;Ответ:x = (-1)к + 1 п/4 + пk, k
;Ответ:x = (-1)к + 1 п/4 + пk, k 
3) 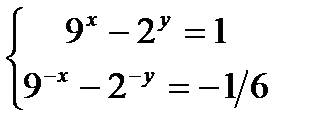
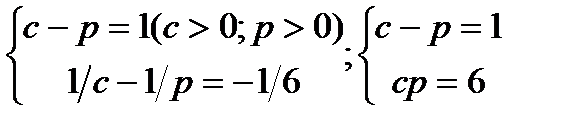 ;c = 3, d = 2илиc = - 2, d = - 3;Ответ:x = 1/2; y = 1
;c = 3, d = 2илиc = - 2, d = - 3;Ответ:x = 1/2; y = 1
4) 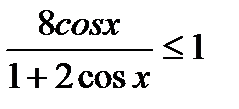 ОДЗ: х
ОДЗ: х 
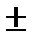 2п/3 + 2пк
2п/3 + 2пк
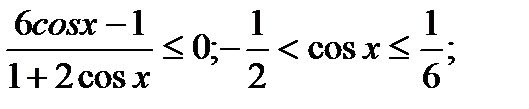
Ответ:x 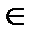 [arccos1/6 + 2пк;2п/3 + 2пк)
[arccos1/6 + 2пк;2п/3 + 2пк)  (4п/3 + 2пк;2п – arccos1/6 + 2пк], k
(4п/3 + 2пк;2п – arccos1/6 + 2пк], k 
5*)cos2x – (р – 2)cosx + 4р + 1 = 0- ПАРАМЕТРЫ
СПОСОБ.
cosx = t; 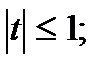 t2 – (p – 2)t + 4p + 1 = 0; D = p2 – 20p = p(p – 20);D< 0 прир
t2 – (p – 2)t + 4p + 1 = 0; D = p2 – 20p = p(p – 20);D< 0 прир 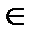 (0; 20) –
(0; 20) – 
D  0;
0; 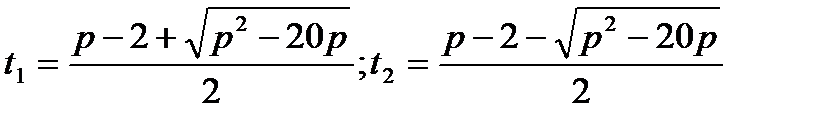
Уравнениенеимееткорней (D  0) втрёхслучаях. Рассмотрим3системы.
0) втрёхслучаях. Рассмотрим3системы.
1) 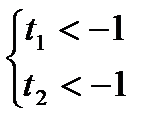
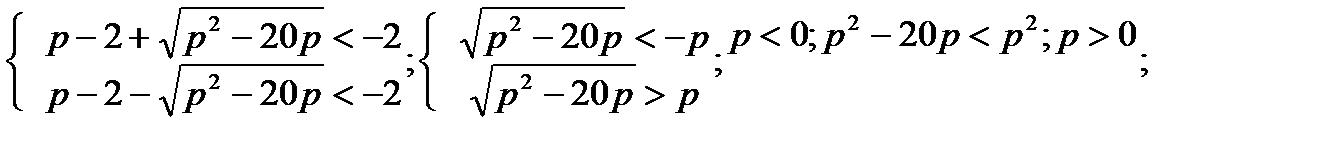 Ответ:
Ответ: 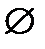
2) 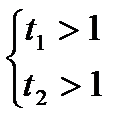
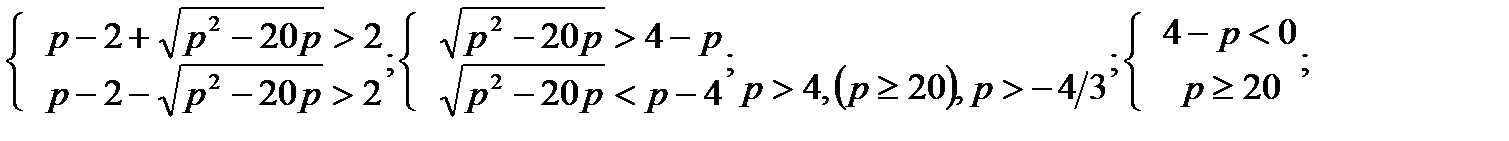 р
р  20
20
3) 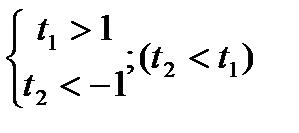
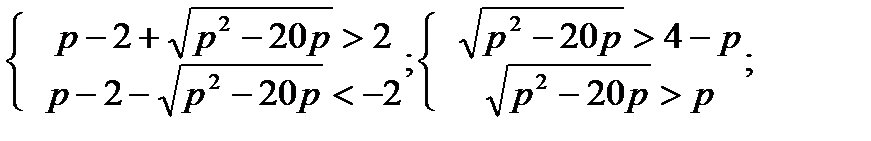 Ответ: р <
Ответ: р < 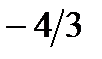
а)р < 0,р2 – 20р > 16 – 8р + р2, р < - 4/3
б)р  4,(р
4,(р  20), р2 – 20р > р2, р < 0,
20), р2 – 20р > р2, р < 0, 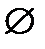
в)р 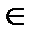
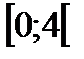 ,
,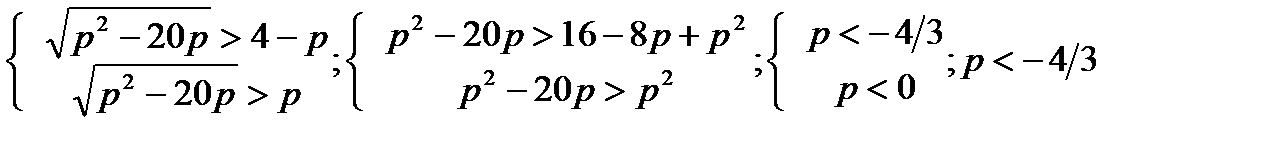 ;
; 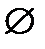
Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0
СПОСОБ.
cosx = t; 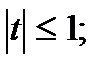 t2 – (p – 2)t + 4p + 1 = 0
t2 – (p – 2)t + 4p + 1 = 0
t2 – pt + 2t + 4p + 1 = 0; (t + 1)2 = p(t – 4); 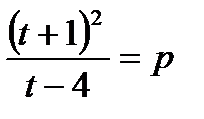
Рассмотримфункциюy(t) = 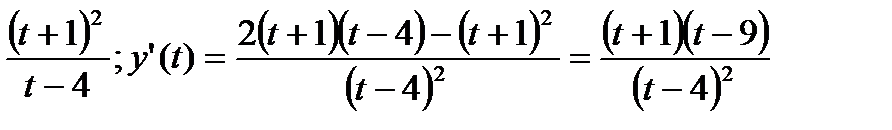 ;
;
y = p+-+у'(t)
t-119y(t)
-101 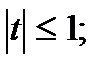 функцияубывает; f( - 1) = 0; f( 1) = - 4/3
функцияубывает; f( - 1) = 0; f( 1) = - 4/3
Рассмотримпрямуюy = pивозможностьеёпересеченияс
-4/3даннымграфиком.
Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0
3СПОСОБ.y
cosx = t; 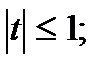 t2 – (p – 2)t + 4p + 1 = 0y = (t + 1)2
t2 – (p – 2)t + 4p + 1 = 0y = (t + 1)2
t2 – pt + 2t + 4p + 1 = 0; (t + 1)2 = p(t – 4);4
Рассмотрим 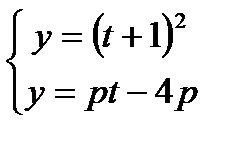 y =
y = 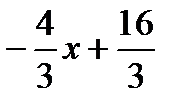
а)р > 0, 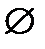
б)р = 0, 1 решениеt
в)р < 0 ( y(1) = 4, pt-4p = 0 при t = 4. См. рис.)-3-1014
Составимуравнениепрямой, проходящейчерезточки(1;4) и (4;0)y = - 4/3 x + 16/3
Следовательно, нетрешенийприk< - 4/3 ( уголнаклонасположительнымнаправлениемосиабсциссстановитьсяменьше)
Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0
СПОСОБ.
cosx = t;  t2 – (p – 2)t + 4p + 1 = 0
t2 – (p – 2)t + 4p + 1 = 0
D = p2 – 20p = p(p – 20);D< 0 прир 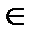 (0; 20) – решенийнет
(0; 20) – решенийнет
Рассмотримфункциюy(t) = t2 – (p – 2)t + 4p + 1
Функция не пересекает ось Оt при 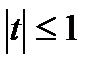 в трёх случаях (Д
в трёх случаях (Д  0, t2<t1). Рассм.3системы.
0, t2<t1). Рассм.3системы.
y( - 1) = 5p; y( 1) = 3p + 4; t0 = 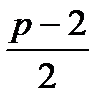 ; D
; D  0 – лишнееусловие
0 – лишнееусловие
1) 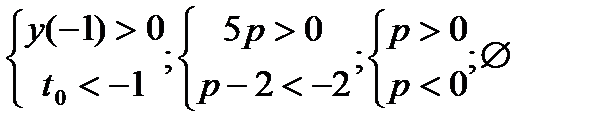
t
t2t1 -1
2) 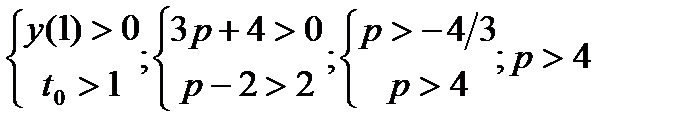
t
1t2t1
3) 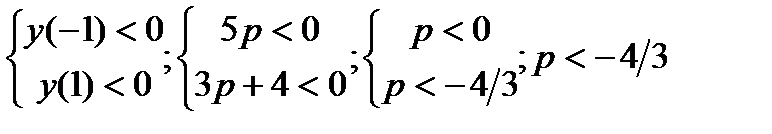
-11tОтвет: уравнениенеимееткорнейпри р < - 4/3; р > 0
t2t1
