Основныеспособырешенияпоказательныхуравнений

Оглавление

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ.. 2

РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ НЕРАВЕНСТВ.. 5

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ.. 6

РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ.. 10

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.. 12

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ.. 18

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.. 21

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ.. 31

ЭКЗАМЕНАЦИОННАЯ РАБОТА – ПАРАМЕТРЫ.. 34

ОСНОВНЫЕСПОСОБЫРЕШЕНИЯПОКАЗАТЕЛЬНЫХУРАВНЕНИЙ

1)Уравнениявидаa^{f (x)} = 1(a> 0; a 1).Решение:f(x) = 0

а) ;ОДЗ: х -2;2Ответ: х = -2/3

б) ;ОДЗ: х 1; х 7/3

; х = 5/3Ответ: х = 5/3

2)Уравнениявидаa^{f (x)} = a^p(x)(a> 0; a 1).Решение:f(x) = р(х)

а) Ответ: х = 1

б) ; Ответ: х = 4

в) ;ОДЗ: х 0

Ответ: х = 3;-1/5

г) ;ОДЗ: х 0;

Ответ: х = 81

д) ; Ответ: х = 3

е)2^{2 + 4 + 6 +…+ 2х} = (0,25) ^{– 15}

2 + 4 + … + 2х = 30; 1 + 2 +…+ х = 15 – ар.пр. S =

х² + х – 30 = 0; x = -6; 5 (-6 – не подходит по смыслу задачи)Ответ: х = 5

Уравнения, вкоторых впоказателестепенипереднеизвестнымстоитодини тотжекоэффициент,решаютсявынесением заскобкуобщегомножителя (чащенаименьшего)

3^{2х – 5} + 3^{2х – 7} + 3^{2х – 9} = 91

3^{2х – 9}(3⁴ + 3² + 1) = 91; 3^{2х – 9} = 1;х = 4,5Ответ: х = 4,5

4)Уравнениявида:a^{f (x)} = b^{f (x)}(a> 0; b> 0; a 1; b 1; a b).Решение: (a/b)^{f (x)} = 1

а) ; Ответ: решенийнет

б)2^{8 – х} + 7^{3 – х} = 7^{4 – х} + 2^{3 – х}

2^{3 – х}(2⁵ – 11) = 7^{3 – х}(7 – 1); (2/7)^{3 – х} = 6/21; 3 – х = 1; х = 2Ответ: х = 2

в)

Ответ: х =

Уравнения,сводящиесякквадратным.

а)

б) ОДЗ:

Ответ: х = 1,5

в)2^3х + 8 - 6 = 0

2^х(2^2х - 6 + 8) = 0; 2^х 0; 2^х = 2; х = 1; 2^х = 4; х = 2Ответ: х = 1; х = 2

г) Ответ: х = 0

Однородныеуравнения.

а)2 - 3 - 5 = 0

(2/5)^2х - (2/5)^х – 5 = 0;Д = 49; (2/5)^х -1; (2/5)^х = 5/2; х = -1Ответ: х = -1

б)10^2/х + 25^1/х = 50^1/х;ОДЗ: х 0

(10/5)^2/х – 17/ (10/5)^1/х + 1 = 0;Д = 225;2^1/х = 4; х = 1/2;2^1/х = 1/4;х = -1/2Ответ:х =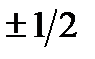

в) ;ОДЗ: х 0

Ответ: х =

7)Уравнениявидаa^{f (x)} = b^{р (x)}(a> 0; b> 0; a 1; b 1; a b)решаютсялогарифмированиемобеихчастейпоодномуоснованию.

а)1 сп.)2^{х – 3} = 3^х

lg2^{х – 3} = lg 3^х; (x – 3)lg2 = xlg3; x = Ответ: х =

2 cп.)2^{х – 3} = 3^х; Ответ: х = (привести к одному показателю)

б)

в)

г)

Нестандартныеспособырешения.

а)2^3х - ;Ответ: х = 1

б) (Разделить на )

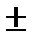Ответ: х = 2

в) - «завуалированное» обратное число

Ответ: х =

г) - использование монотонности

единственный корень уравненияОтвет: х =

д) - использование монотонности

Уравнение имеет не более одного корнях = 1- проверка подтверждает.Ответ: х = 1

е) - использование монотонности

Уравнение имеет не более одного корнях = 1- проверка подтверждает.Ответ: х = 1

ж)

1) х = 0 – левая часть не имеет смысла

2) ;Ответ: х =

з)

1) х = 1 – левая и правая части не имеют смысла

2) Ответ: х = 0; х = 2; х = 4

РЕШЕНИЕПОКАЗАТЕЛЬНЫХНЕРАВЕНСТВ

Методы решения анaлогичны. Обязательно учитывать основание.

1) ;ОДЗ: х - 4;Ответ: х

2) Ответ: х > 2

3)4^х - 5^2х – 10^х> 0

(2/5)^2x – (2/5)^x – 2 > 0; (2/5)^x< -1; (2/5)^x> 2; x<log_2/52Ответ: х <log_2/52

4)7^{х +2}- 7^{х + 1} + 7^х>60

7^х (49-21 + 2) >60; 7^х>60; 7^х>2; Ответ:

5)5^{2x + 1} + 6^{x + 1}> 30 +

5^2x(5 – 6^x) - 6(5 – 6^x) > 0; (5 – 6^x)(5^2x – 6) > 0Ответ: х

6) ; ( )Ответ: х

7) ; ОДЗ: х 0

Ответ: х

8)

Ответ: х =

ОСНОВНЫЕСПОСОБЫРЕШЕНИЯЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ

При использовании формул: слева направо возможно сужение области определения. Следовательно, возможна потеря корней. Такое применение этих формул не рекомендуется.

При использовании этих формул справа налево возможно расширение области определения. Следовательно, возможно появление посторонних корней.Следовательно, необходимо делать проверку или находить ОДЗ.

1)Уравнения, решаемыеспомощьюопределениялогарифма.

а)log₃(x – 12) = 2; ;x = 21;Ответ: х = 21

б)log₁₁log₃log₂ = 0; (ОДЗ:х ) Отв:

Уравнения c логарифмами разных оснований приводятся к одному основанию.

а) ОДЗ:х > 0; (4log₃x = 6; log₃x = 3/2)Ответ: х = 3

б)log₃x + 2log_x3 = 3;ОДЗ:х > 0; x 1

log₃x = h;h + 2/h = 3;h = 1; x =3; h = 2; x = 9;Ответ: х = 3; x = 9

Замена переменных.

а)

Отв: х = 3

б) .

, где . Тогда , . , , .

Рассмотрим три случая: 1) .- а + 1 - а + 2 = 1,a= 1, 1 Ï [0;1)2) .а - 1 - а + 2 = 1, [1; 2)3) .а - 1 + а - 2 = 1, а=2

Решение: [1; 2].Если , то , , .Ответ: .

в)

Метод интервалов

Алгоритм:1) ОДЗ

2) Решить уравнениеf(x) = g(x)

3) Подставить в исходное неравенство по одному значению из каждого изполучившихся интервалов (знаки не обязательно чередуются)

Если проверяемое значение удовлетворяет неравенству, то и все остальные значения соответствующего промежутка ему удовлетворяют.

Если проверяемое значение не удовлетворяет неравенству, то и никакое другое значение соответствующего промежутка ему не удовлетворяют.

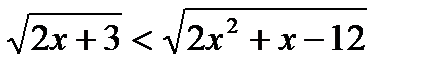
ОДЗ: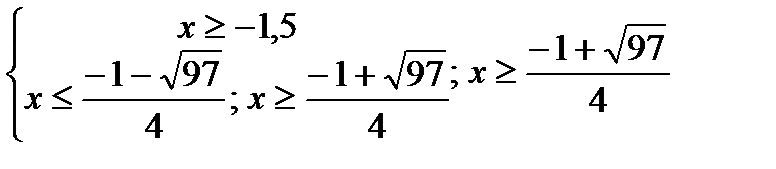

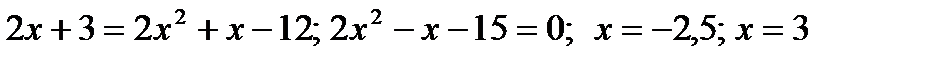
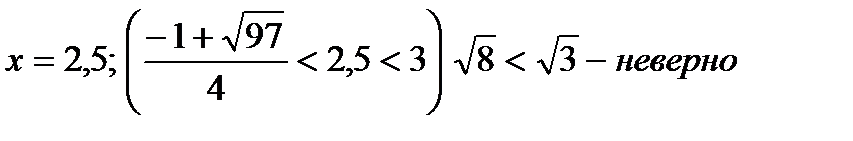
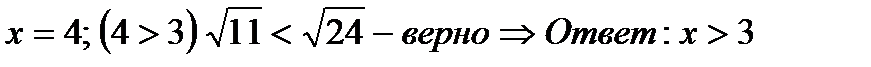
Частныеслучаииобщиеформулы.

а)sinx = 0;x = пk, k sinx = 1;x = п/2 + 2пk, k sinx = -1;x = -п/2 + 2пk, k sinx = d, 0 <d< 1;x = (-1)каrcsind + пk, k sinx = d, -1 <d< 0;x = (-1)к +1аrcsin(- d) + пk, k б)сosx = 0;x = п/2 + пk, k cosx = 1;x = 2пk, k cosx = -1;x = п + 2пk, k cosx = d, 0 < d < 1;x = аrccosd + 2пk, k

в)tgx = d, d > 0;x = аrctgd + пk,k tgx = d, d < 0;x = -аrctg(-d) + пk, k г)ctgx = d, d > 0;x = аrcctgd + пk, k ctgx = d, d < 0;x = -аrcctg(-d) + пk, k

Квадратные уравнения

а)

б) (При решении ОДЗ не расширяется. Не находить)

4)

Возьмём sin от обеих частей уравнения.

РЕШЕНИЕ1ВАРИАНТА.

1)log _1/2(3x + 5) log 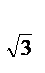3ОДЗ: х > - 5/3

3x + 5 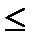1/4; х 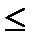- 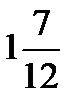;Ответ:x 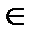(-1 ; - ]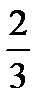

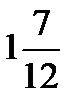2)sin²x - 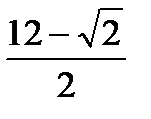sinx - 3 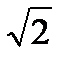= 0

D = (6 + 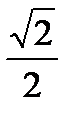)²;sinx = 6; - 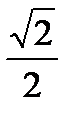;Ответ:x = (-1)^{к + 1} п/4 + пk, k

3)

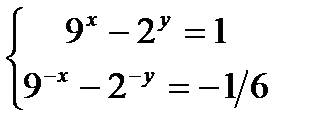
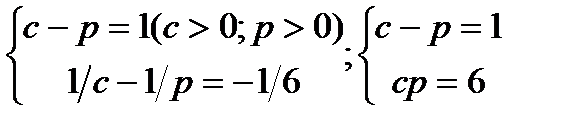;c = 3, d = 2илиc = - 2, d = - 3;Ответ:x = 1/2; y = 1

4) 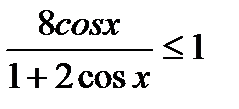ОДЗ: х 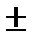2п/3 + 2пк

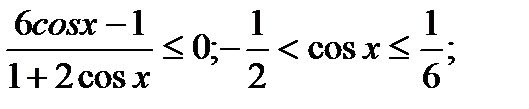
Ответ:x 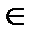[arccos1/6 + 2пк;2п/3 + 2пк) (4п/3 + 2пк;2п – arccos1/6 + 2пк], k

5*)cos²x – (р – 2)cosx + 4р + 1 = 0- ПАРАМЕТРЫ

СПОСОБ.

cosx = t; 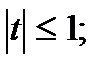t² – (p – 2)t + 4p + 1 = 0; D = p² – 20p = p(p – 20);D< 0 прир 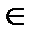(0; 20) –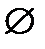

D 0;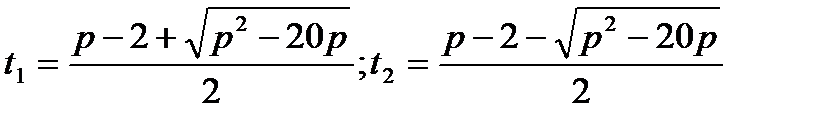

Уравнениенеимееткорней (D 0) втрёхслучаях. Рассмотрим3системы.

1)

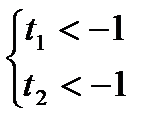
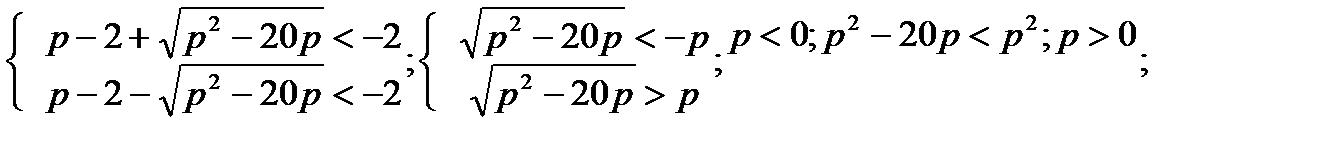Ответ: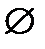

2)

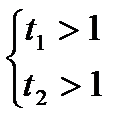
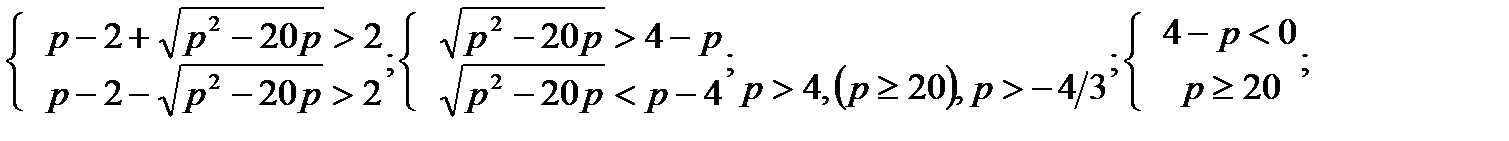р 20

3)

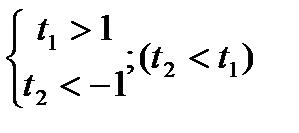
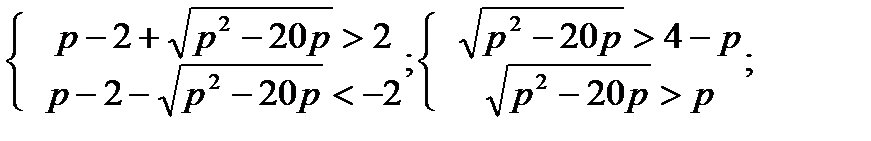Ответ: р <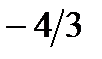

а)р < 0,р² – 20р > 16 – 8р + р², р < - 4/3

б)р 4,(р 20), р² – 20р > р², р < 0,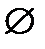

в)р ,;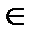

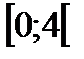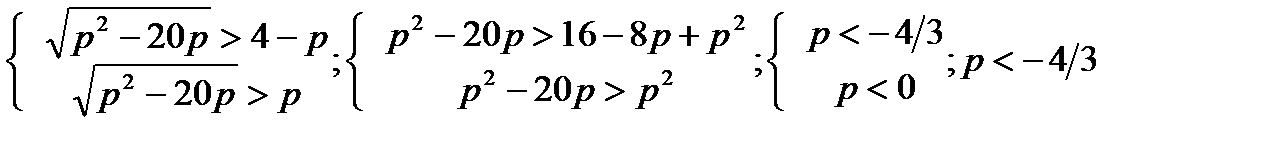Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0

СПОСОБ.

cosx = t; 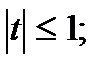t² – (p – 2)t + 4p + 1 = 0

t² – pt + 2t + 4p + 1 = 0; (t + 1)² = p(t – 4);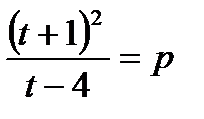

Рассмотримфункциюy(t) = ;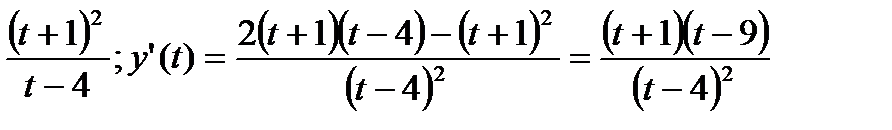

y = p+-+у'(t)

t-119y(t)

-101 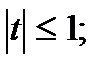функцияубывает; f( - 1) = 0; f( 1) = - 4/3

Рассмотримпрямуюy = pивозможностьеёпересеченияс

-4/3даннымграфиком.

Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0

3СПОСОБ.y

cosx = t; 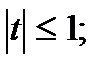t² – (p – 2)t + 4p + 1 = 0y = (t + 1)²

t² – pt + 2t + 4p + 1 = 0; (t + 1)² = p(t – 4);4

Рассмотрим 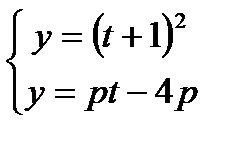y =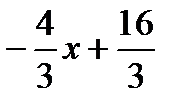

а)р > 0,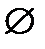

б)р = 0, 1 решениеt

в)р < 0 ( y(1) = 4, pt-4p = 0 при t = 4. См. рис.)-3-1014

Составимуравнениепрямой, проходящейчерезточки(1;4) и (4;0)y = - 4/3 x + 16/3

Следовательно, нетрешенийприk< - 4/3 ( уголнаклонасположительнымнаправлениемосиабсциссстановитьсяменьше)

Ответ: уравнениенеимееткорнейпри р < - 4/3; р > 0

СПОСОБ.

cosx = t; 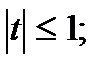t² – (p – 2)t + 4p + 1 = 0

D = p² – 20p = p(p – 20);D< 0 прир 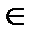(0; 20) – решенийнет

Рассмотримфункциюy(t) = t² – (p – 2)t + 4p + 1

Функция не пересекает ось Оt при 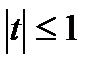в трёх случаях (Д 0, t₂<t₁). Рассм.3системы.

y( - 1) = 5p; y( 1) = 3p + 4; t₀ = 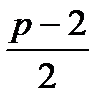; D 0 – лишнееусловие

1)

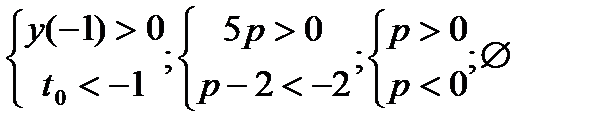
t

t₂t₁ -1

2)

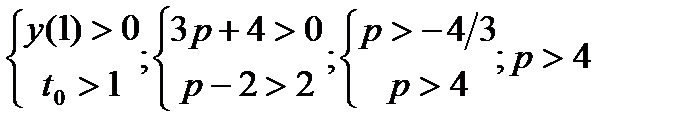
t

1t₂t₁

3)

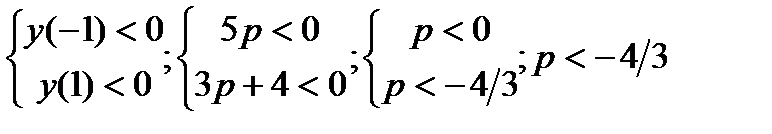
-11tОтвет: уравнениенеимееткорнейпри р < - 4/3; р > 0

t₂t₁

Оглавление

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ.. 2

РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ НЕРАВЕНСТВ.. 5

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ.. 6

РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ.. 10

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.. 12

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ.. 18

ОСНОВНЫЕ СПОСОБЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.. 21

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ.. 31

ЭКЗАМЕНАЦИОННАЯ РАБОТА – ПАРАМЕТРЫ.. 34

ОСНОВНЫЕСПОСОБЫРЕШЕНИЯПОКАЗАТЕЛЬНЫХУРАВНЕНИЙ

1)Уравнениявидаa^{f (x)} = 1(a> 0; a 1).Решение:f(x) = 0

а) ;ОДЗ: х -2;2Ответ: х = -2/3

б) ;ОДЗ: х 1; х 7/3

; х = 5/3Ответ: х = 5/3

2)Уравнениявидаa^{f (x)} = a^p(x)(a> 0; a 1).Решение:f(x) = р(х)

а) Ответ: х = 1

б) ; Ответ: х = 4

в) ;ОДЗ: х 0

Ответ: х = 3;-1/5

г) ;ОДЗ: х 0;

Ответ: х = 81

д) ; Ответ: х = 3

е)2^{2 + 4 + 6 +…+ 2х} = (0,25) ^{– 15}

2 + 4 + … + 2х = 30; 1 + 2 +…+ х = 15 – ар.пр. S =

х² + х – 30 = 0; x = -6; 5 (-6 – не подходит по смыслу задачи)Ответ: х = 5