Тригонометрические и гиперболические функции
РЯДЫ
Методические указания
по выполнению типового расчета
Омск-2005
Составитель Чурашева Надежда Георгиевна, ст. преподаватель
Печатается по решению редакционно-издательского совета Омского государственного технического университета
Прежде чем приступить к выполнению типового расчета, студентам рекомендуется ознакомиться с содержанием справочного материала, а затем и с примерами решения задач.
Типовой расчет
Задача № 1.Найти сумму ряда.
Задача № 2. Используя признак сравнения сходимости, исследовать ряд на сходимость.
Задача № 3.Используя предельную форму признака сравнения сходимости, исследовать ряд на сходимость.
Задача № 4. Используя признак Даламбера, исследовать ряд на сходимость.
Задача № 5. Используя радикальный признак Коши, исследовать ряд на сходимость.
Задача № 6.Используя интегральный признак Коши, исследовать ряд на сходимость.
Задача № 7. Исследовать на сходимость знакочередующийся ряд.
Задача № 8.Найти радиус сходимости и интервал сходимости степенного ряда.
Задача № 9. Используя дифференцирование и интегрирование степенных рядов, найти сумму и указать область сходимости данного ряда.
Задача № 10. Используя табличные разложения, составить ряд Тейлора по степеням (х–а) для указанной функции и указать область сходимости.
Задача № 11.Вычислить интеграл с точностью 0,0001.
Задача № 12.Найти первые 4 – 5 отличных от нуля членов в разложении решения у(х) дифференциального уравнения в ряд Тейлора по степеням (х–а).
Задача № 13.Разложить данную функцию y = f(x) c периодом 2p, заданную на интервале ]-p,p[, в тригонометрический ряд Фурье.
Задача № 14. Разложить функцию y = f(x), заданную на интервале ]0, l[, в тригонометрический ряд Фурье по косинусам.
Задача № 15. Разложить функцию y = f(x), заданную на интервале ]0; l[, в тригонометрический ряд Фурье по синусам.
| Задача | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
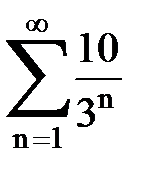 | 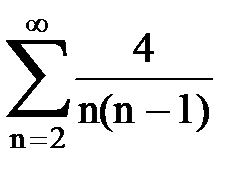 | 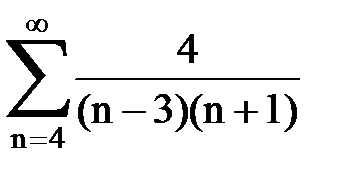 | 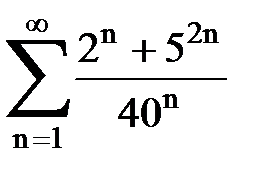 | 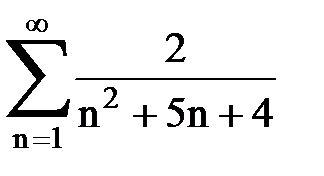 | |
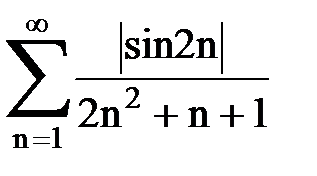 | 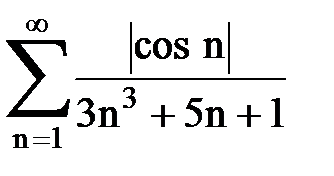 | 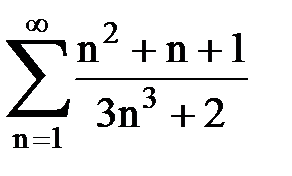 | 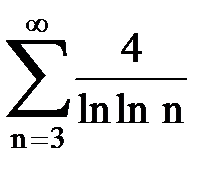 | 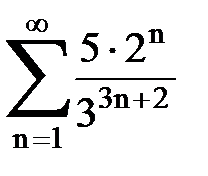 | |
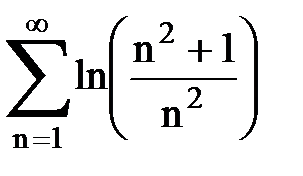 | 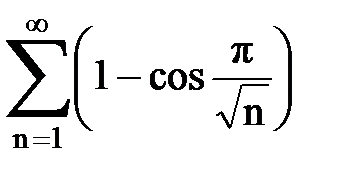 | 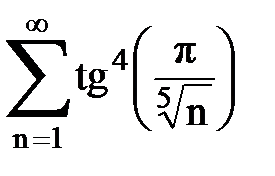 | 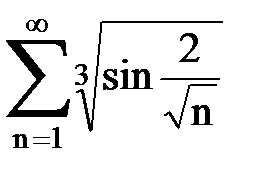 | 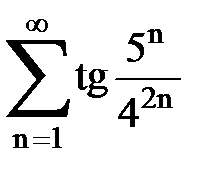 | |
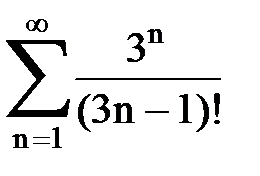 | 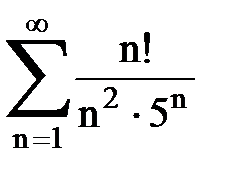 | 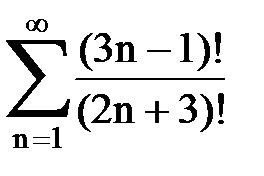 | 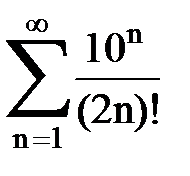 | 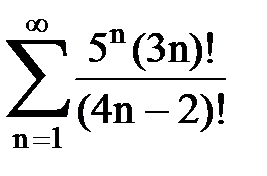 | |
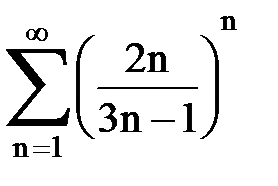 | 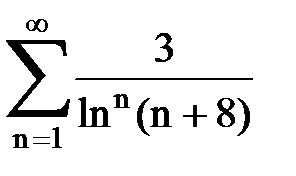 | 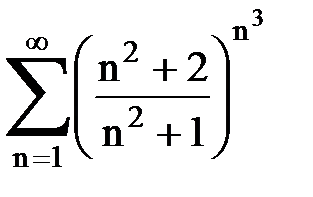 | 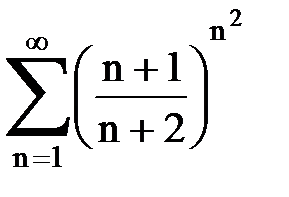 | 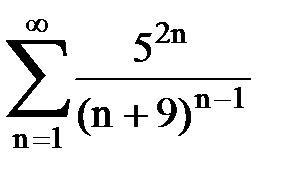 | |
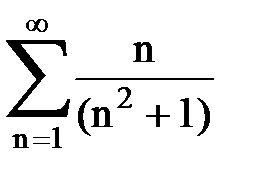 | 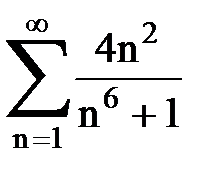 | 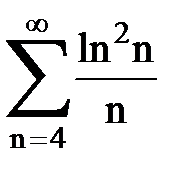 | 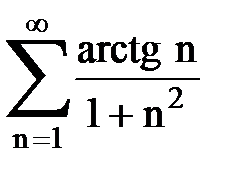 | 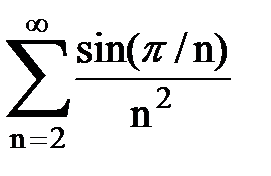 | |
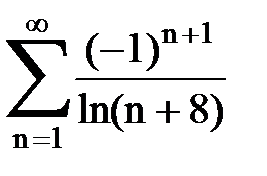 | 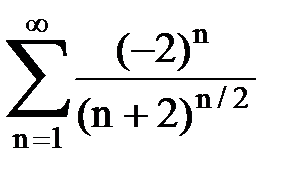 | 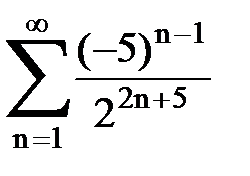 | 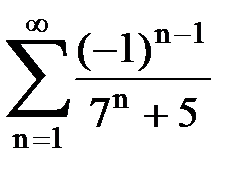 | 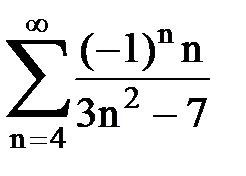 | |
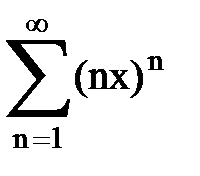 | 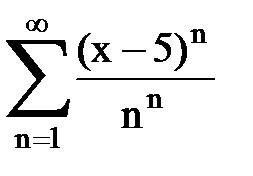 | 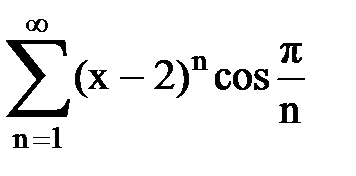 | 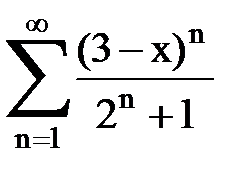 | 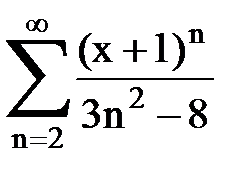 | |
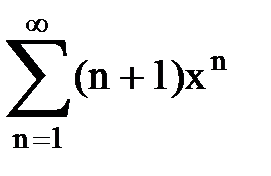 | 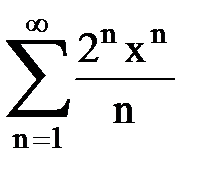 | 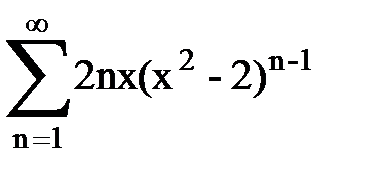 | 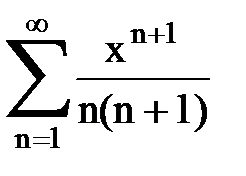 | 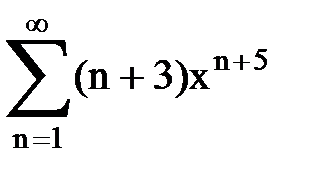 | |
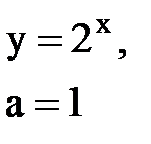 | 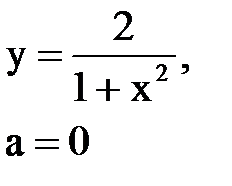 | 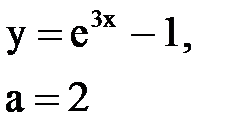 | 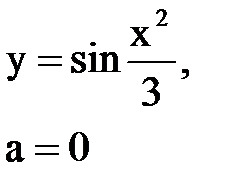 | 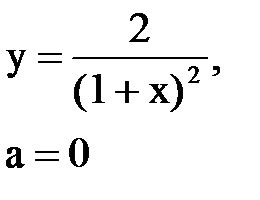 | |
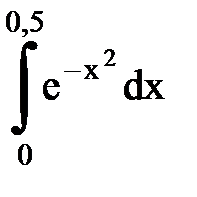 | 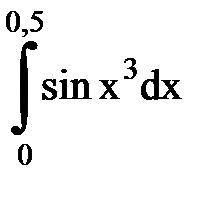 | 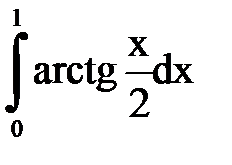 | 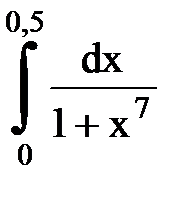 | 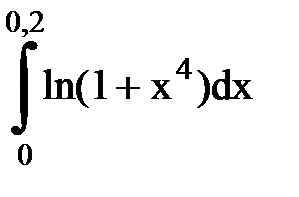 | |
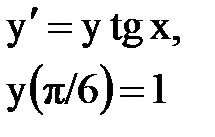 | 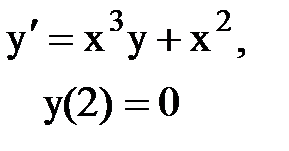 | 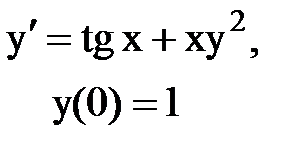 | 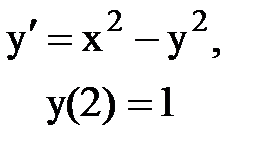 | 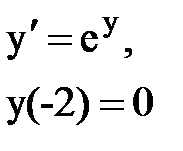 |
| Задача | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
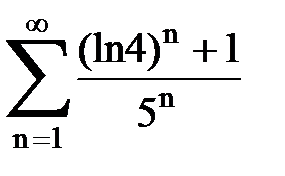 | 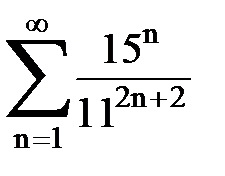 | 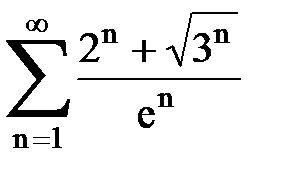 | 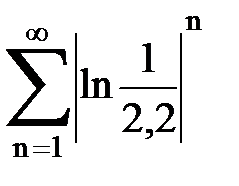 | 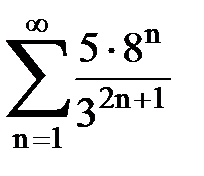 | |
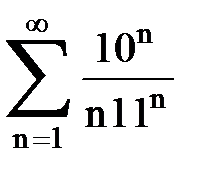 | 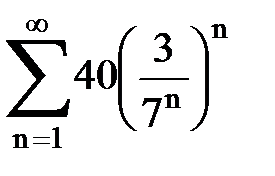 | 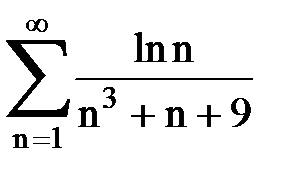 | 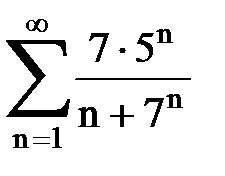 | 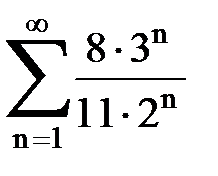 | |
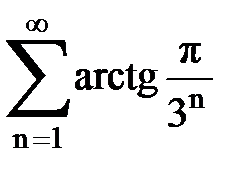 | 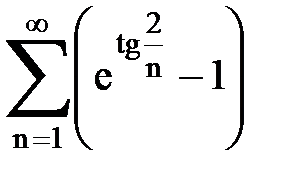 | 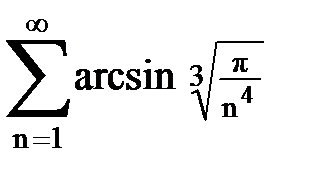 | 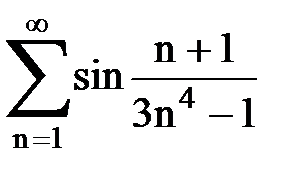 | 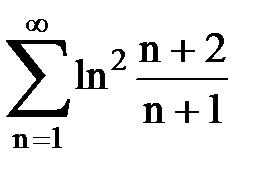 | |
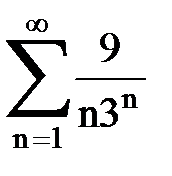 | 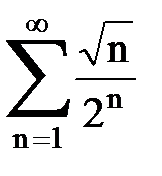 | 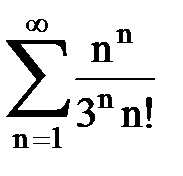 | 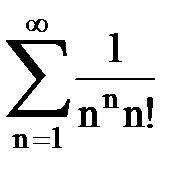 | 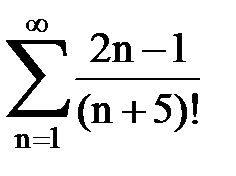 | |
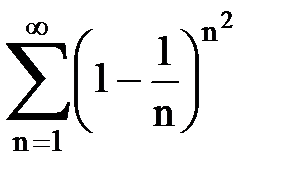 | 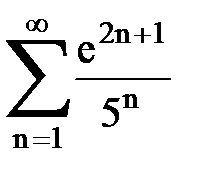 | 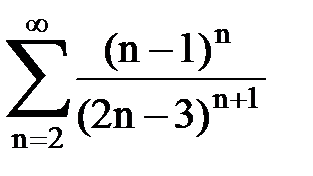 | 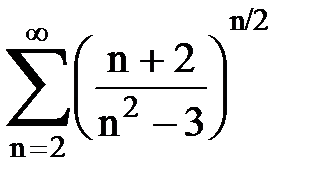 | 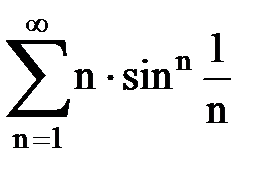 | |
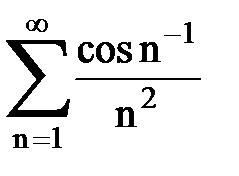 | 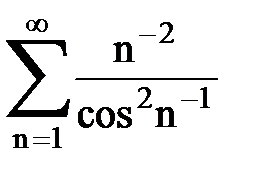 | 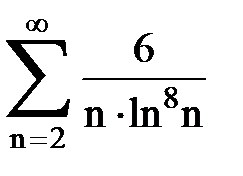 | 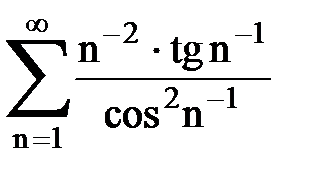 | 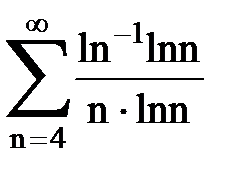 | |
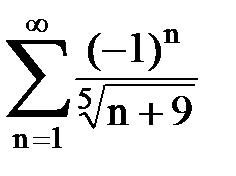 | 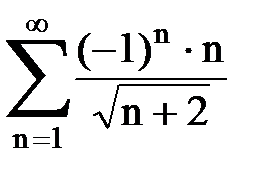 | 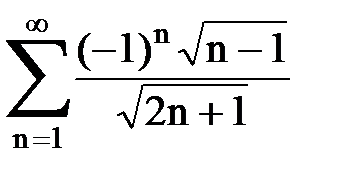 | 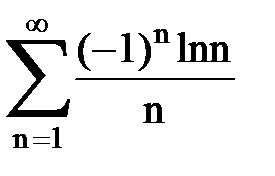 | 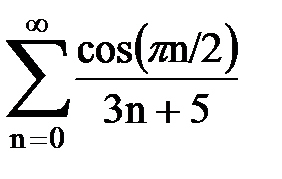 | |
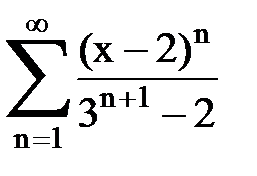 | 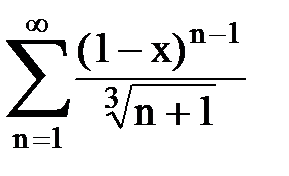 | 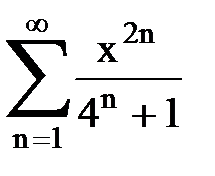 | 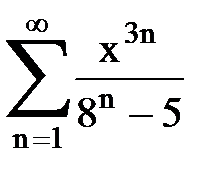 | 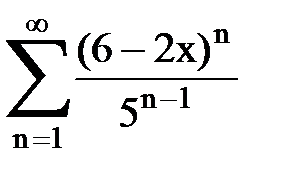 | |
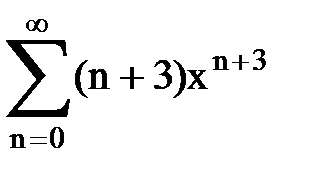 | 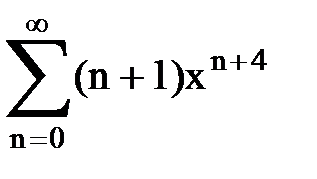 | 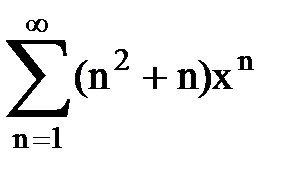 | 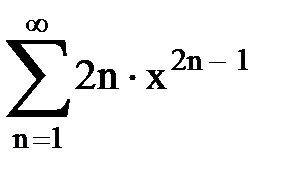 | 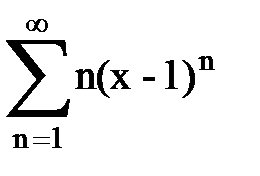 | |
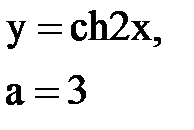 | 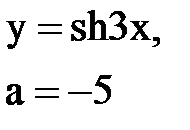 | 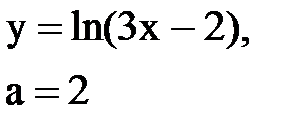 | 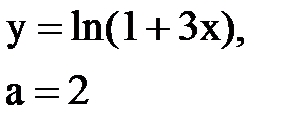 | 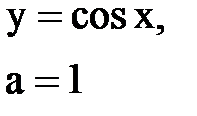 | |
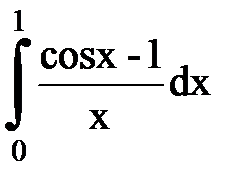 | 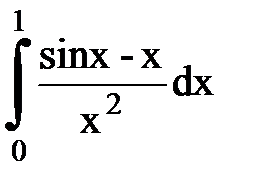 | 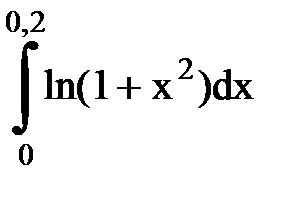 | 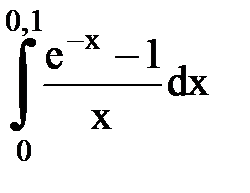 | 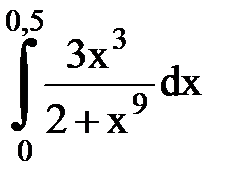 | |
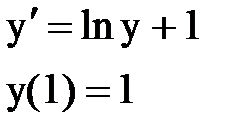 | 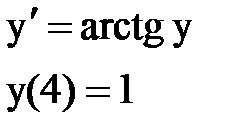 | 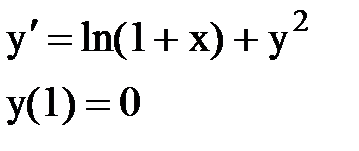 | 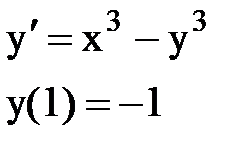 | 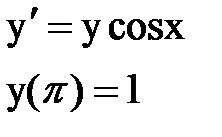 |
| Задача | Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 |
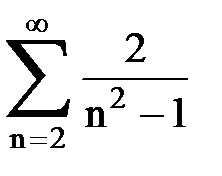 | 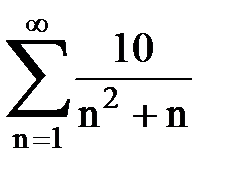 | 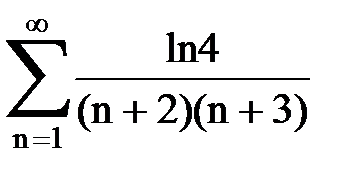 | 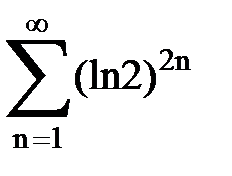 | 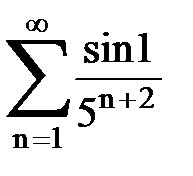 | |
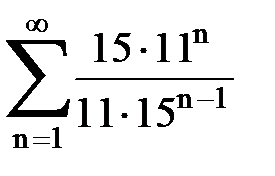 | 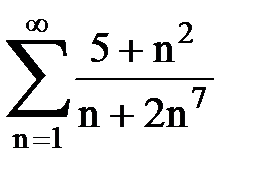 | 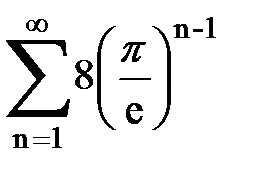 | 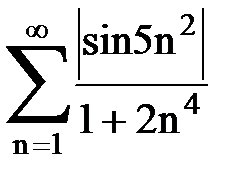 | 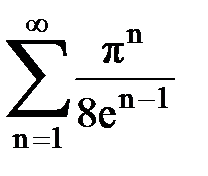 | |
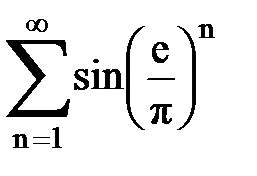 | 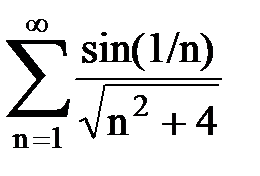 | 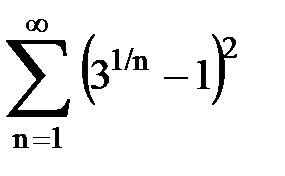 | 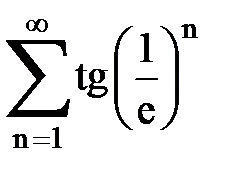 | 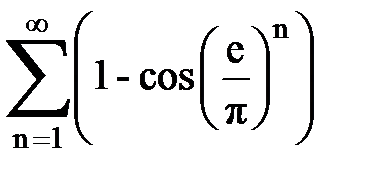 | |
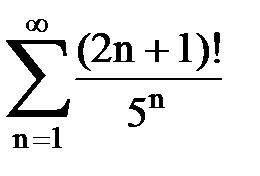 | 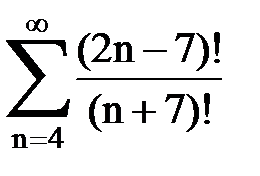 | 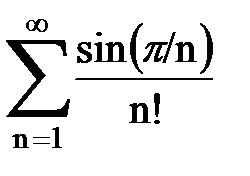 | 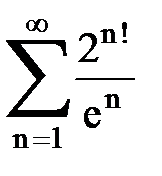 | 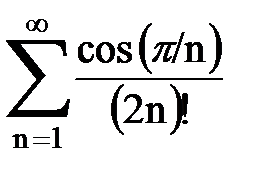 | |
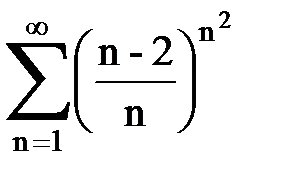 | 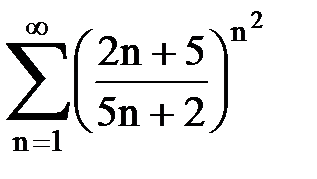 | 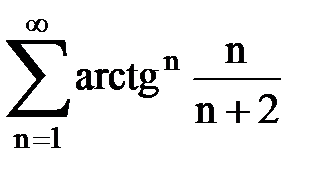 | 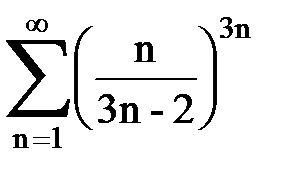 | 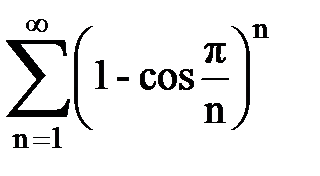 | |
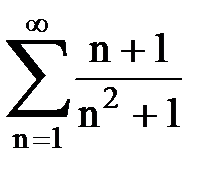 | 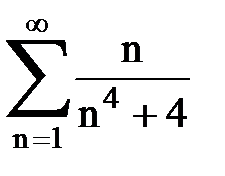 | 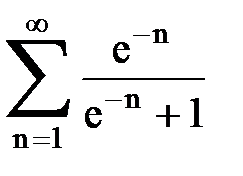 | 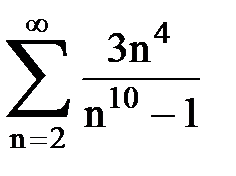 | 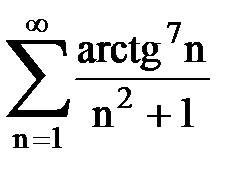 | |
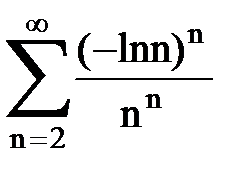 | 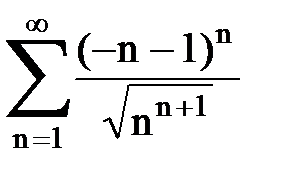 | 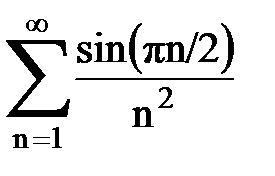 | 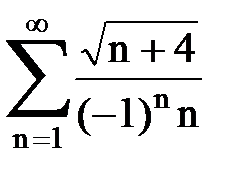 | 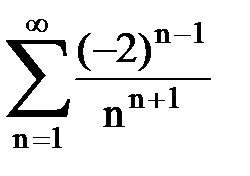 | |
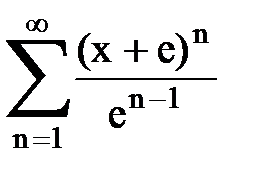 | 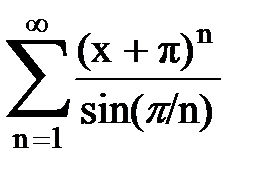 | 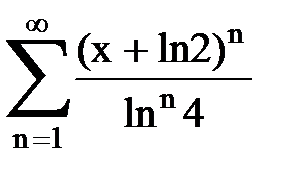 | 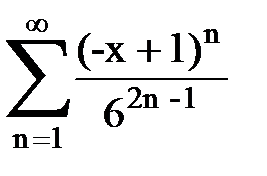 | 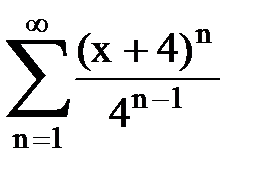 | |
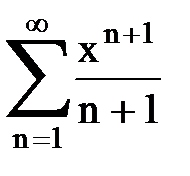 | 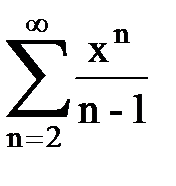 | 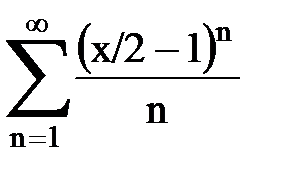 | 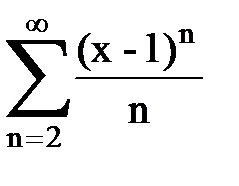 | 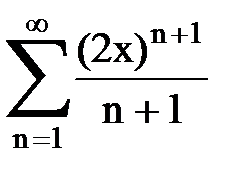 | |
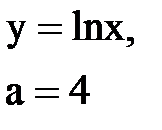 | 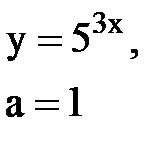 | 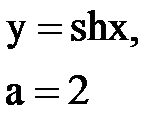 | 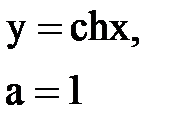 | 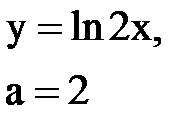 | |
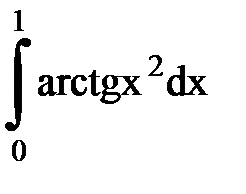 | 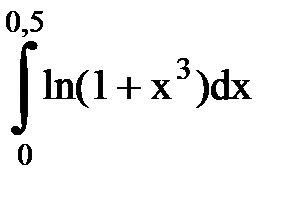 | 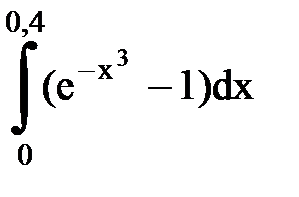 | 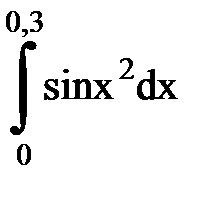 | 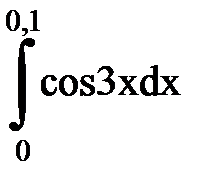 | |
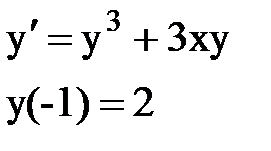 | 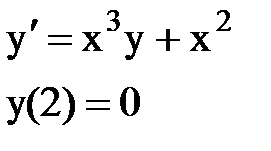 | 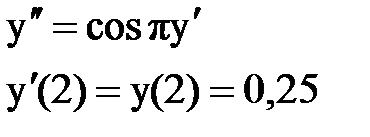 | 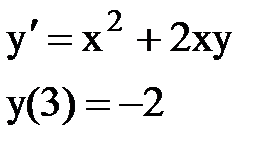 | 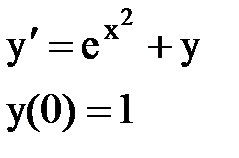 |
| Задача | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
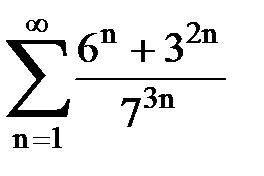 | 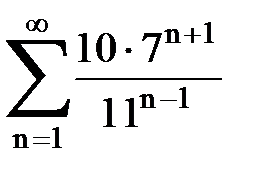 | 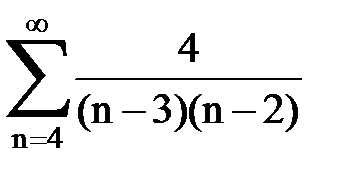 | 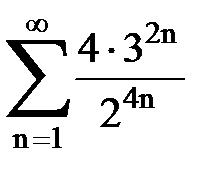 | 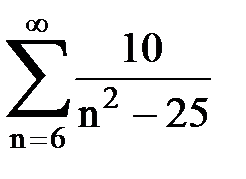 | |
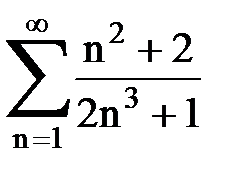 | 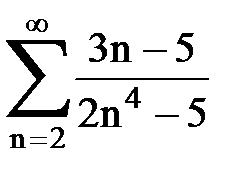 | 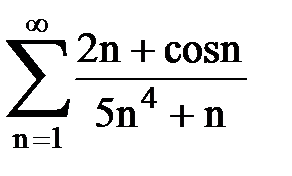 | 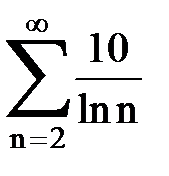 | 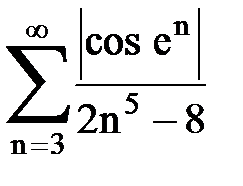 | |
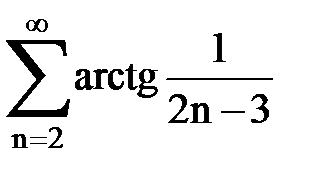 | 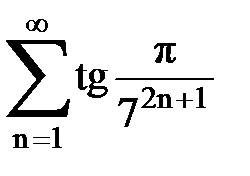 | 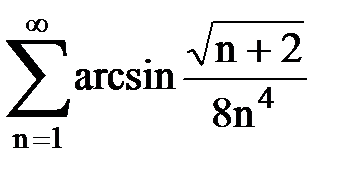 | 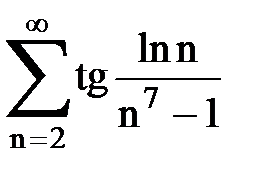 | 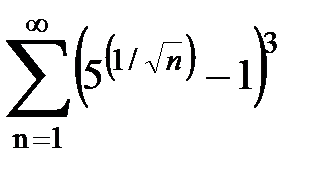 | |
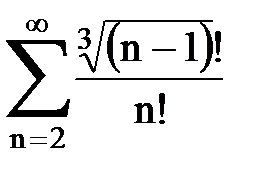 | 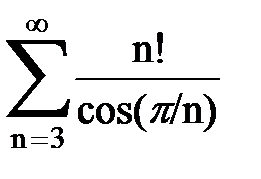 | 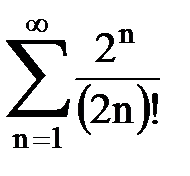 | 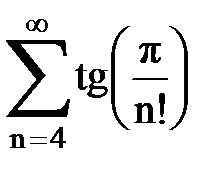 | 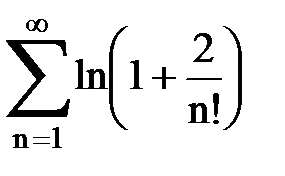 | |
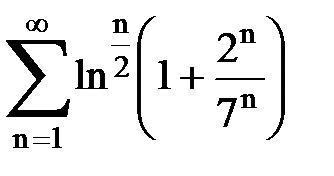 | 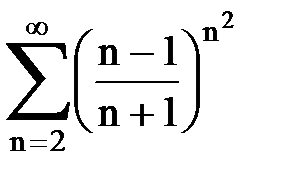 | 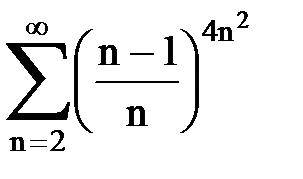 | 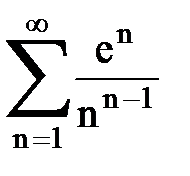 | 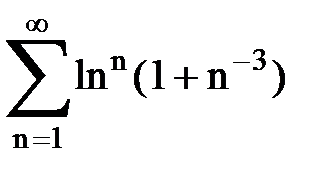 | |
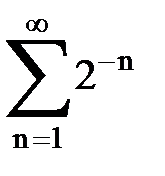 | 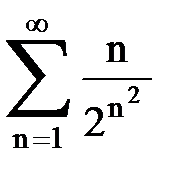 | 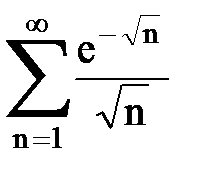 | 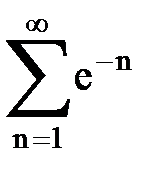 | 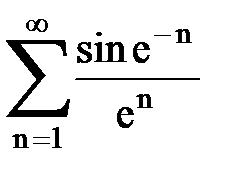 | |
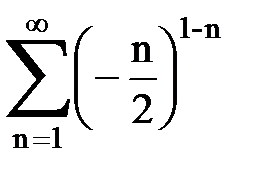 | 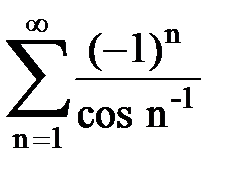 | 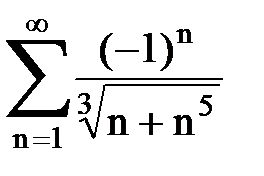 | 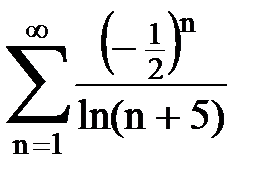 | 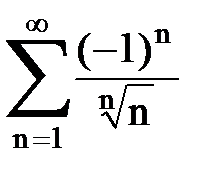 | |
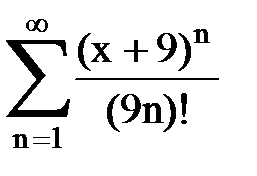 | 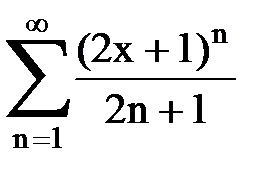 | 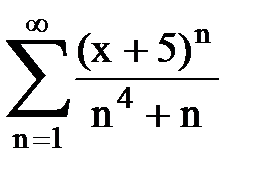 | 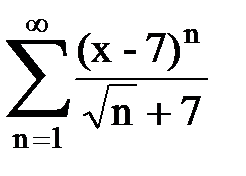 | 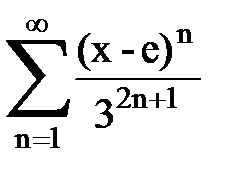 | |
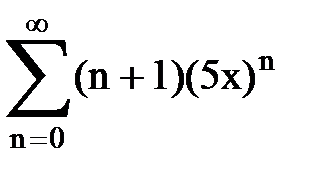 | 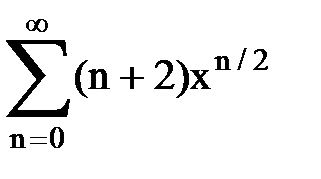 | 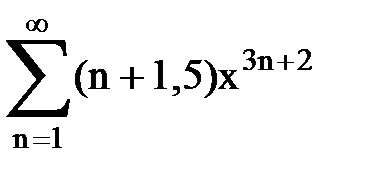 | 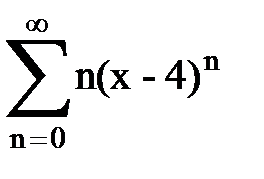 | 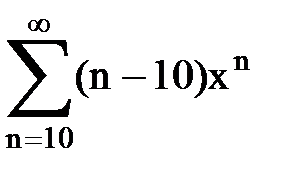 | |
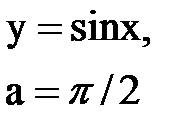 | 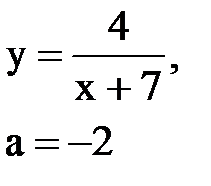 | 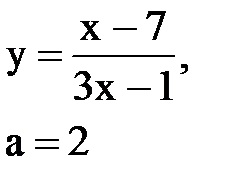 | 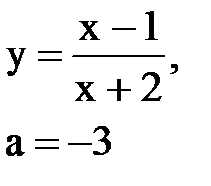 | 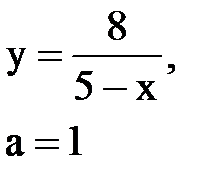 | |
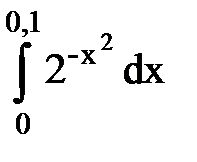 | 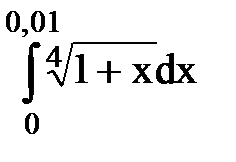 | 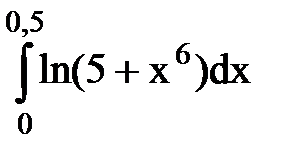 | 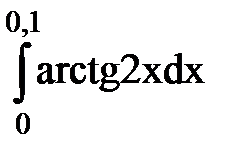 | 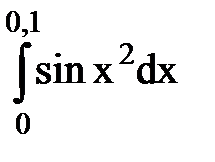 | |
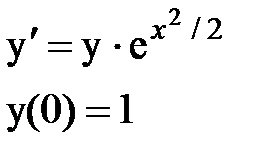 | 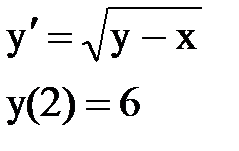 | 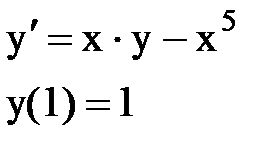 | 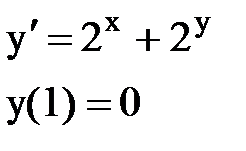 | 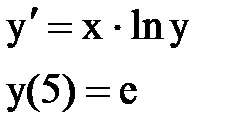 |
| Задача | Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 |
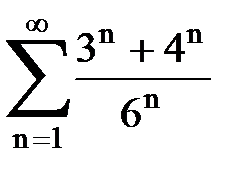 | 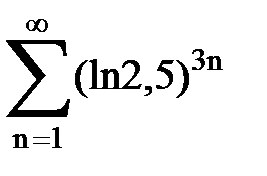 | 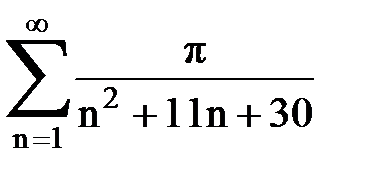 | 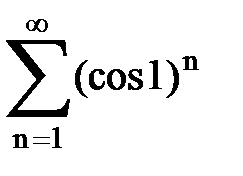 | 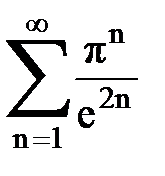 | |
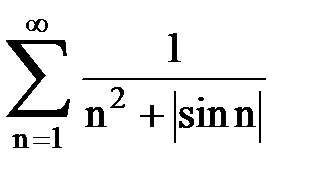 | 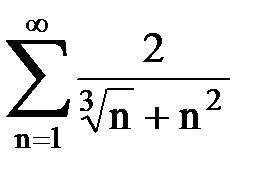 | 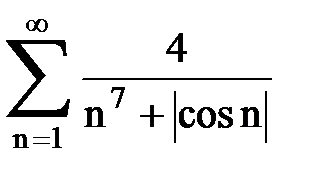 | 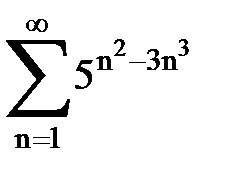 | 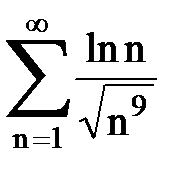 | |
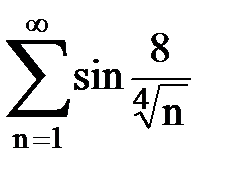 | 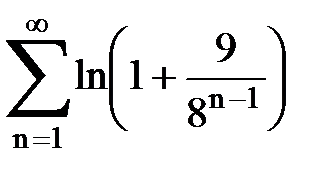 | 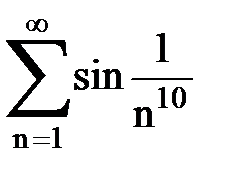 | 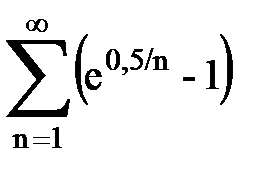 | 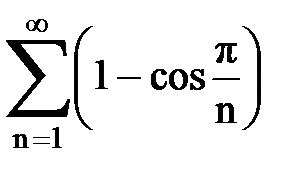 | |
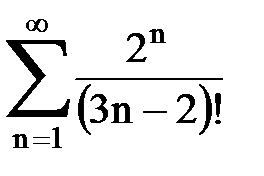 | 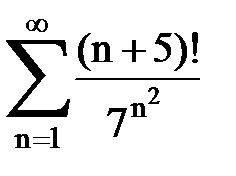 | 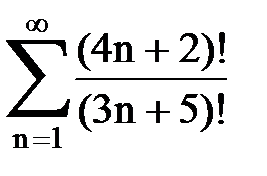 | 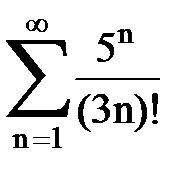 | 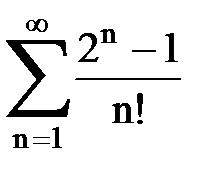 | |
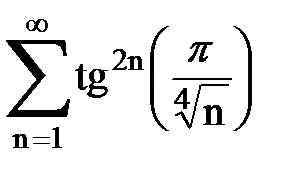 | 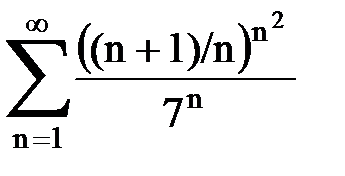 | 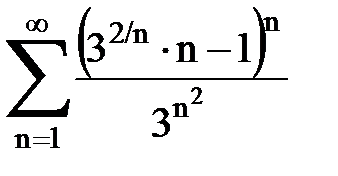 | 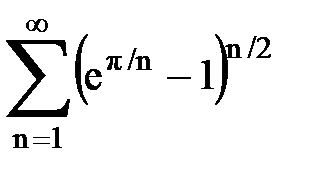 | 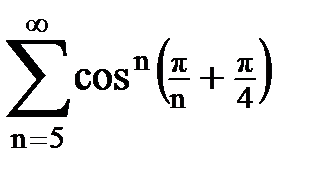 | |
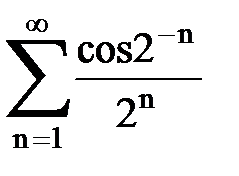 | 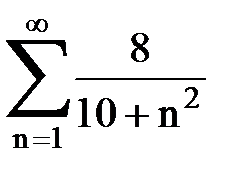 | 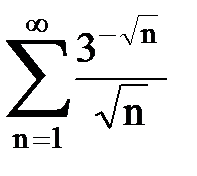 | 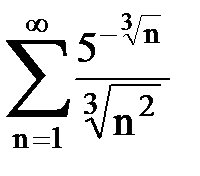 | 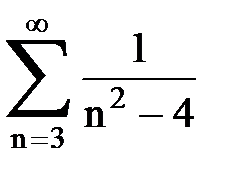 | |
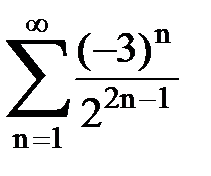 | 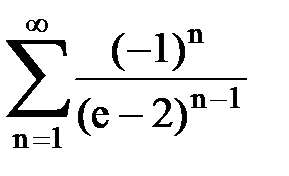 | 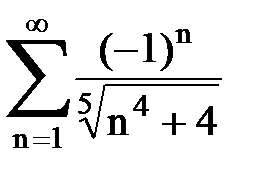 | 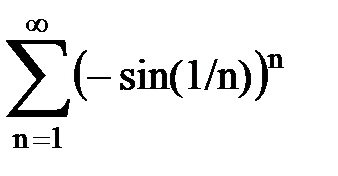 | 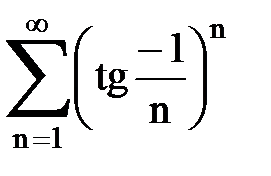 | |
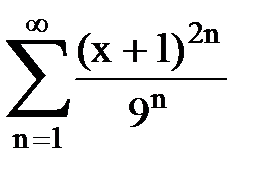 | 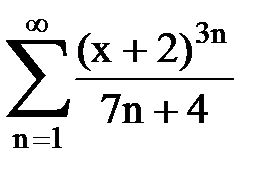 | 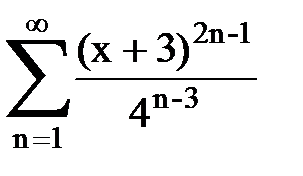 | 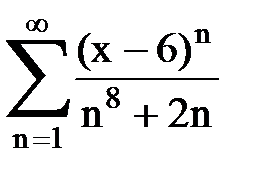 | 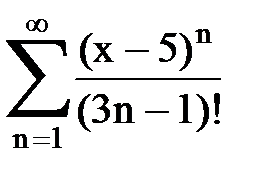 | |
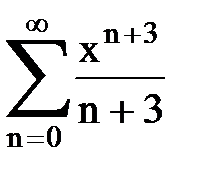 | 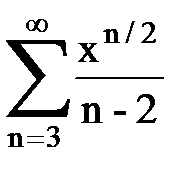 | 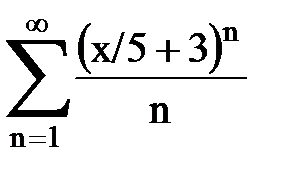 | 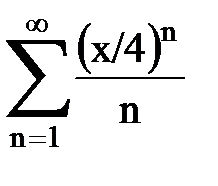 | 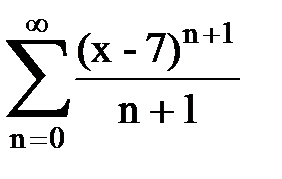 | |
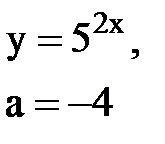 | 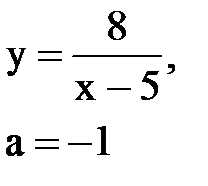 | 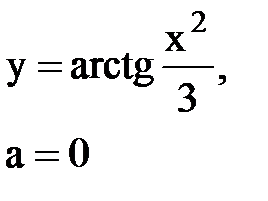 | 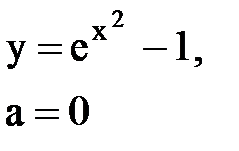 | 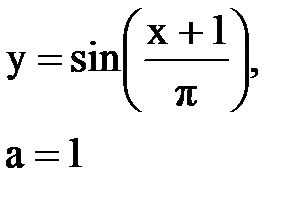 | |
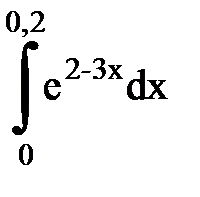 | 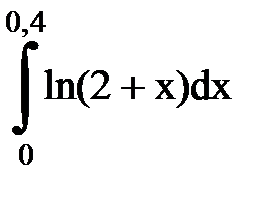 | 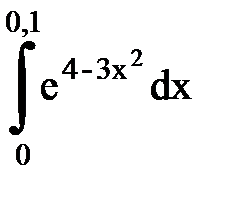 | 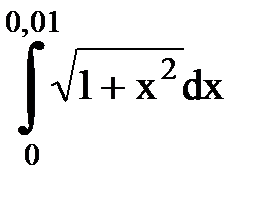 | 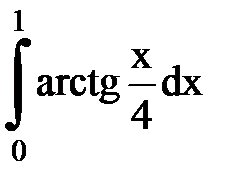 | |
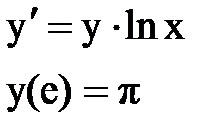 | 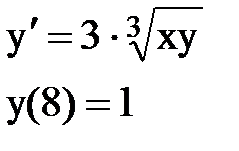 | 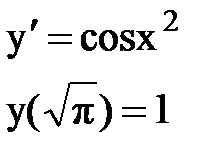 | 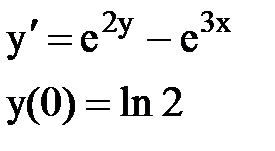 | 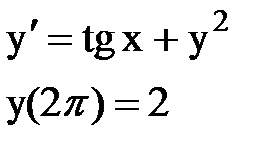 |
| Задача | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
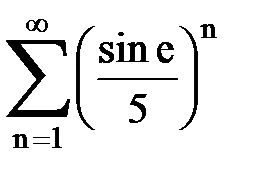 | 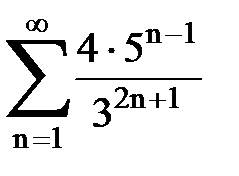 | 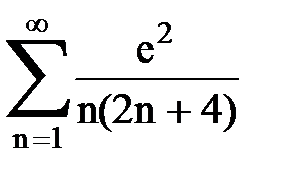 | 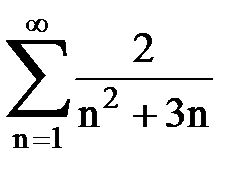 | 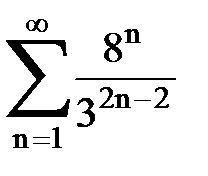 | |
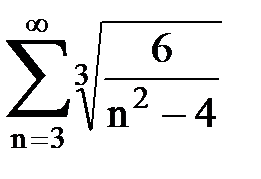 | 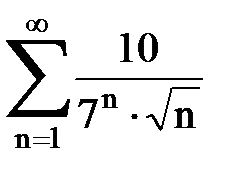 | 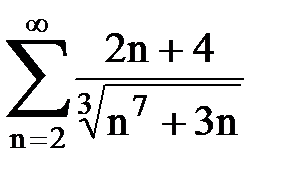 | 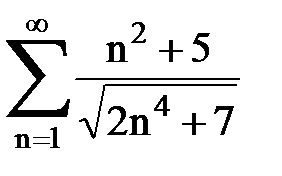 | 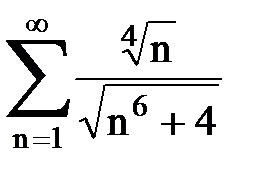 | |
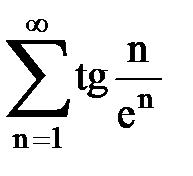 | 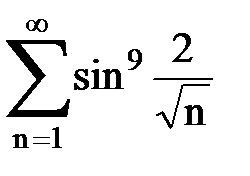 | 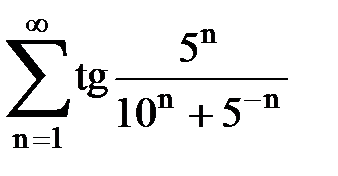 | 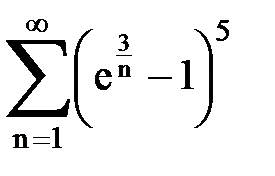 | 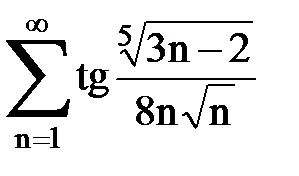 | |
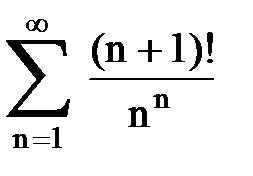 | 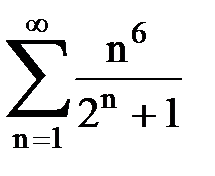 | 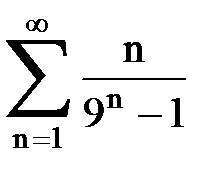 | 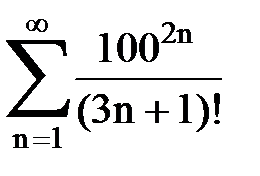 | 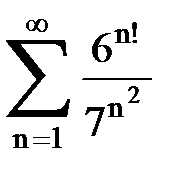 | |
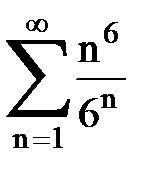 | 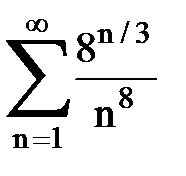 | 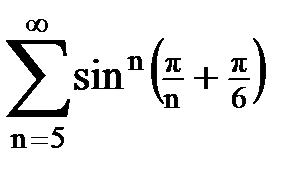 | 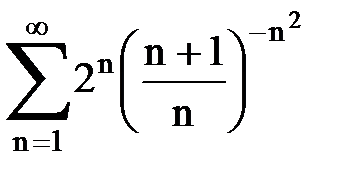 | 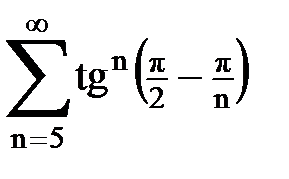 | |
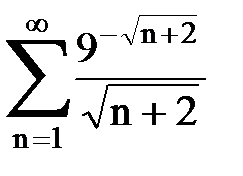 | 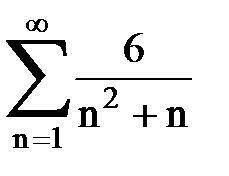 | 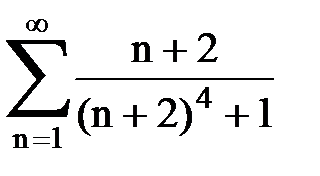 | 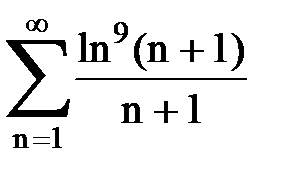 | 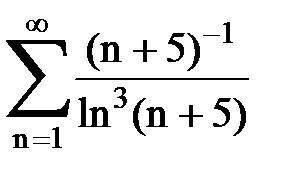 | |
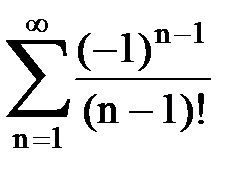 | 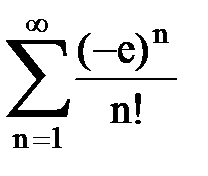 | 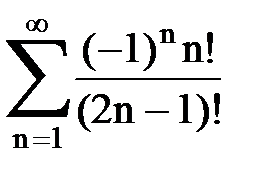 | 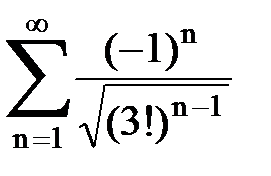 | 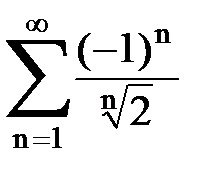 | |
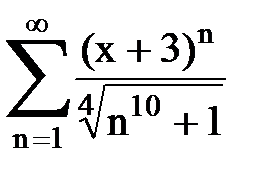 | 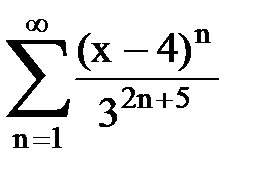 | 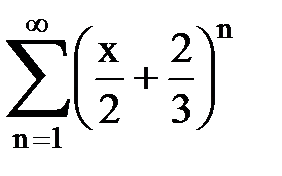 | 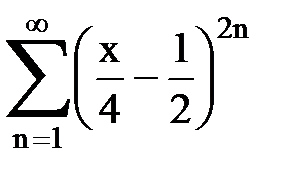 | 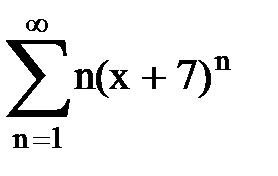 | |
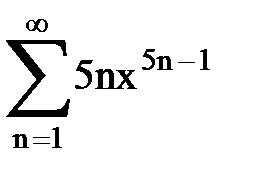 | 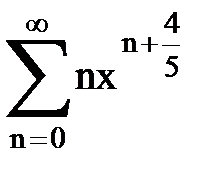 | 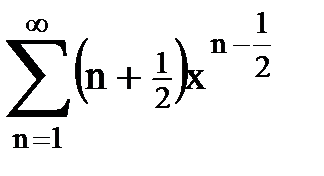 |  | 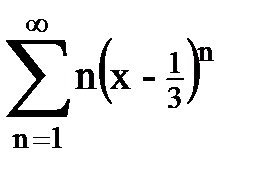 | |
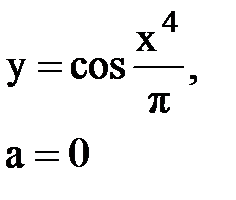 | 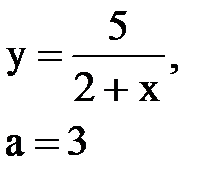 | 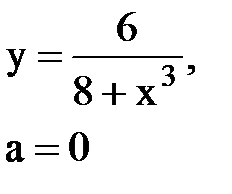 | 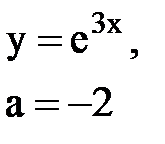 | 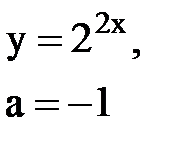 | |
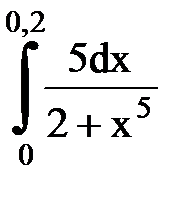 | 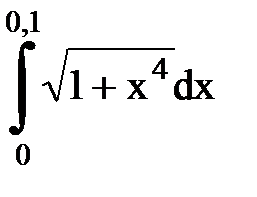 | 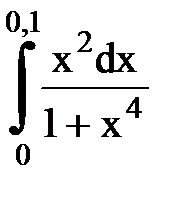 | 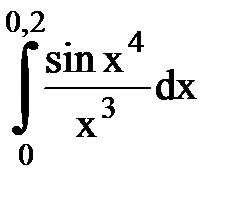 | 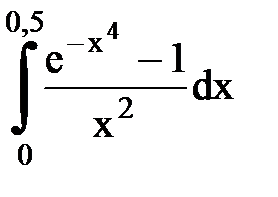 | |
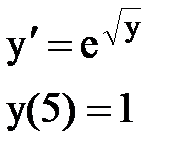 | 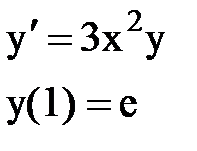 | 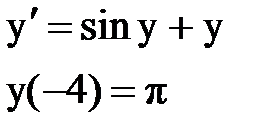 | 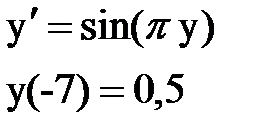 | 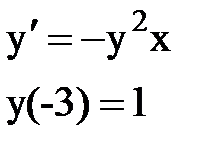 |
| Вари- ант | Задача 13 | Задача 14 | Задача 15 |
| 1. | 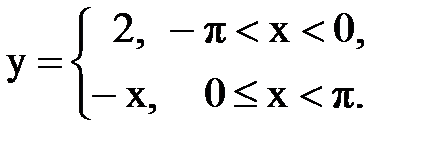 | 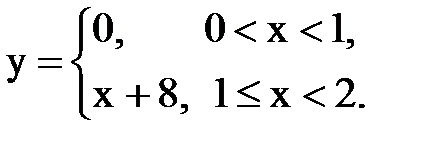 | 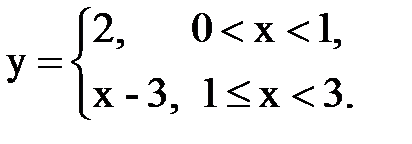 |
| 2. | 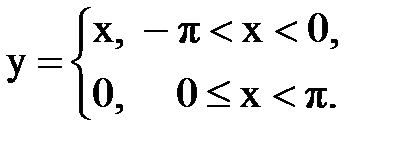 | 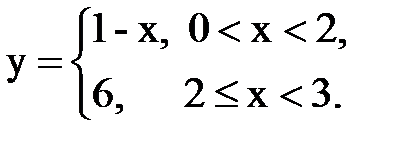 | 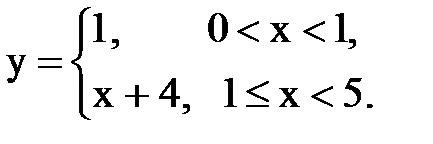 |
| 3. | 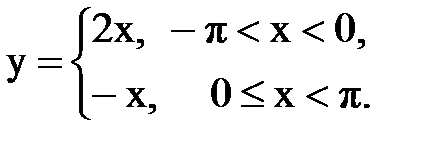 | 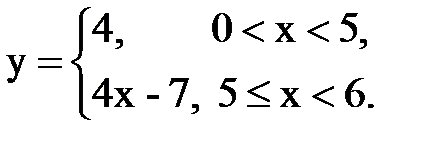 | 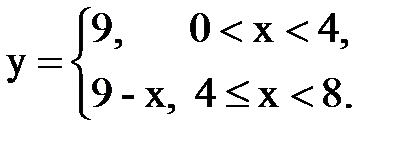 |
| 4. | 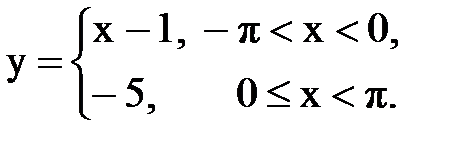 | 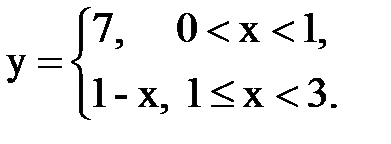 | 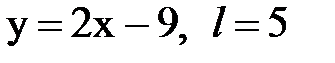 |
| 5. | 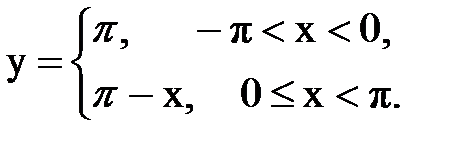 | 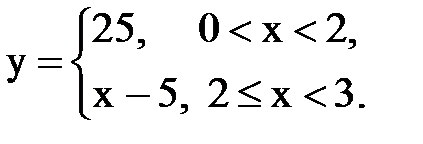 | 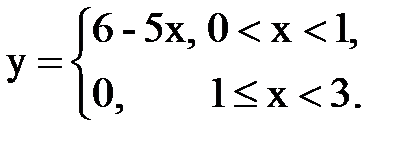 |
| 6. | 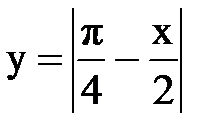 | 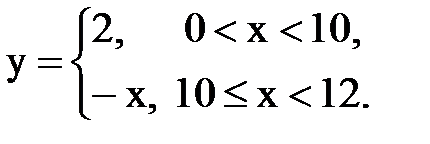 | 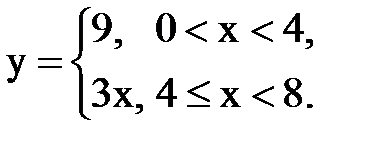 |
| 7. | 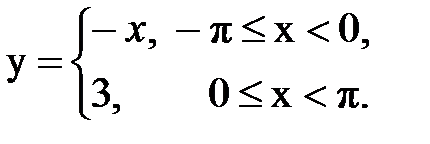 | 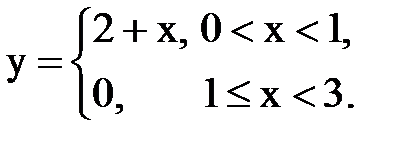 | 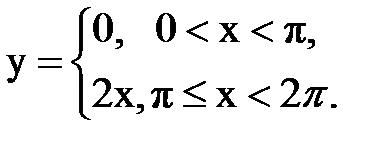 |
| 8. | 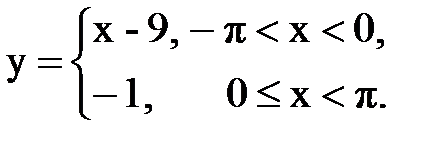 | 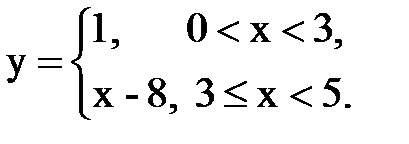 | 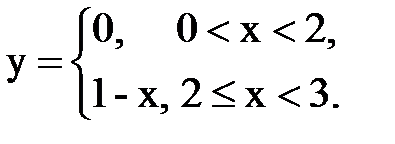 |
| 9. | 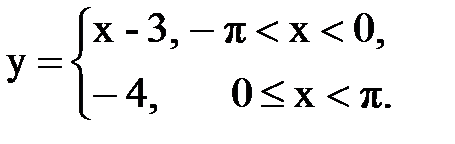 | 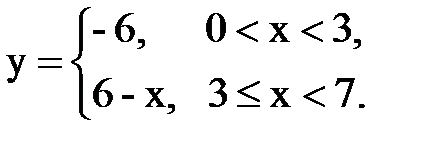 | 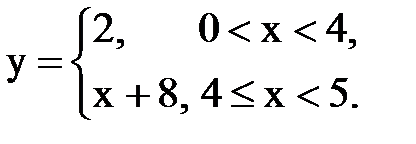 |
| 10. | 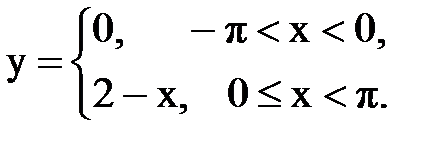 | 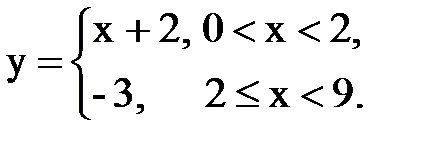 | 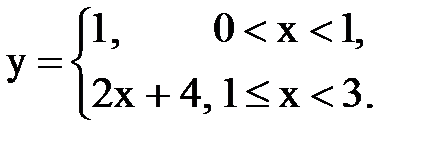 |
| 11. | 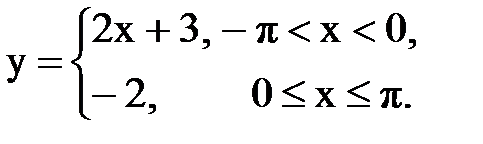 | 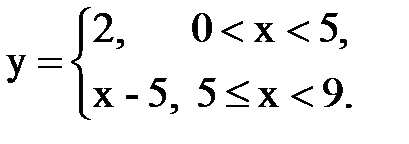 | 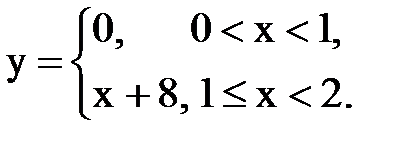 |
| 12. | 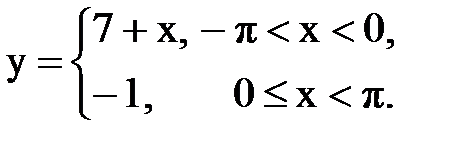 | 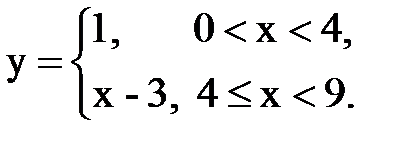 | 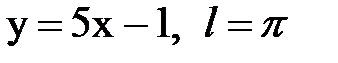 |
| 13. | 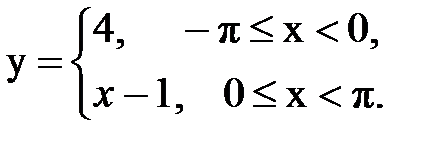 | 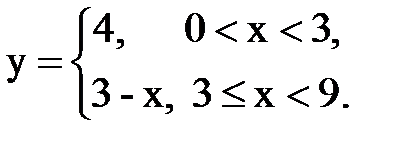 | 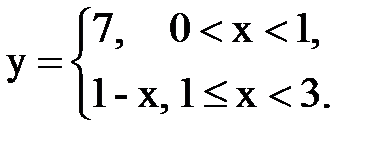 |
| 14. | 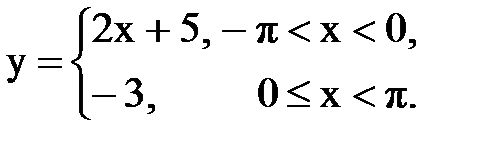 | 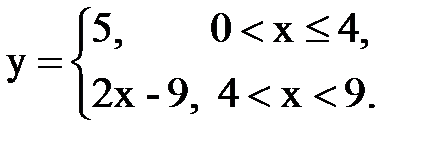 | 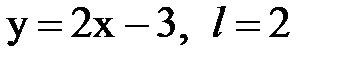 |
| 15. | 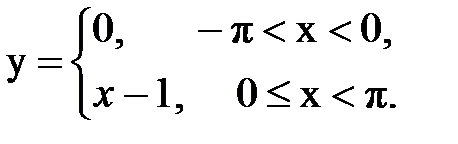 | 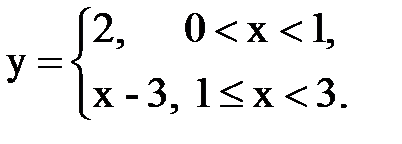 | 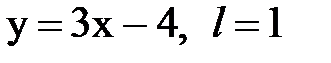 |
| 16. | 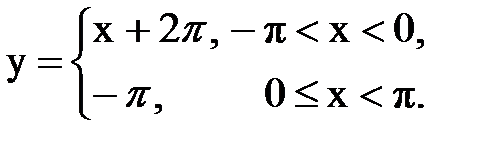 | 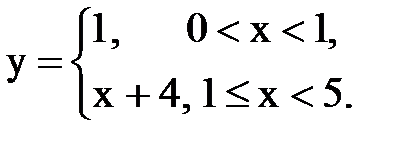 | 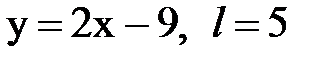 |
| 17. | 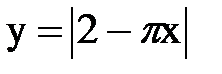 | 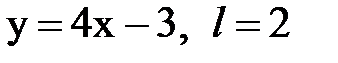 | 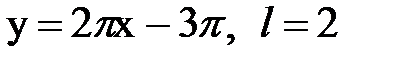 |
| Вари- ант | Задача 13 | Задача 14 | Задача 15 |
| 18. | 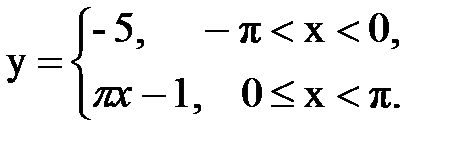 | 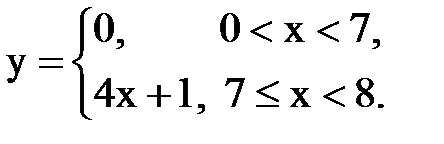 | 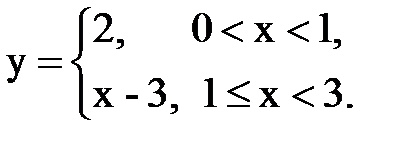 |
| 19. | 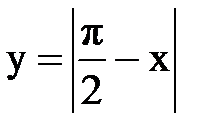 | 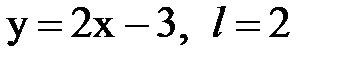 | 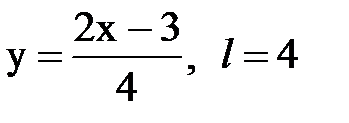 |
| 20. | 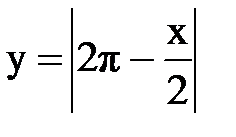 | 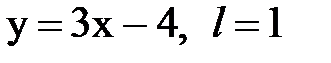 | 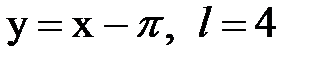 |
| 21. | 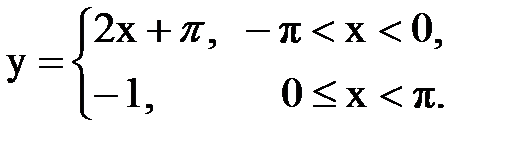 | 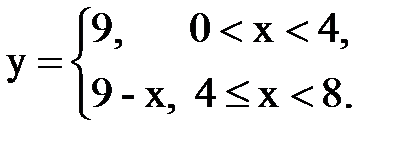 | 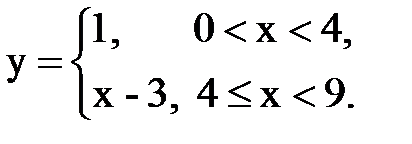 |
| 22. | 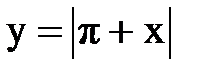 | 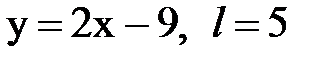 | 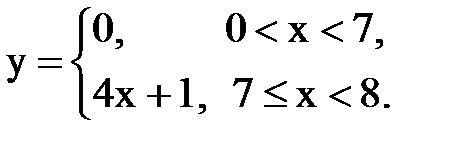 |
| 23. | 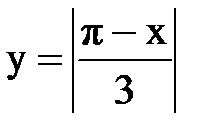 | 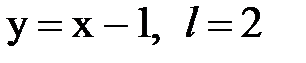 | 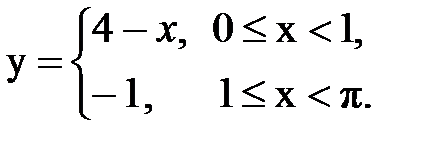 |
| 24. | 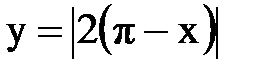 | 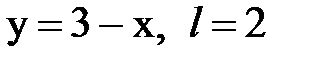 | 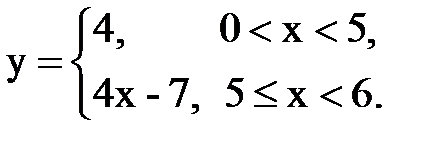 |
| 25. | 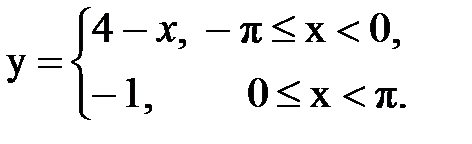 | 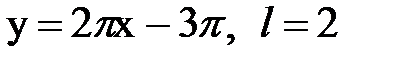 | 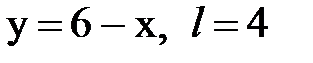 |
| 26. | 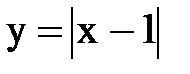 | 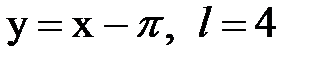 | 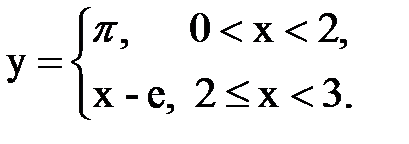 |
| 27. | 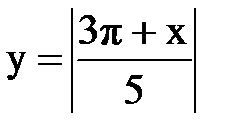 | 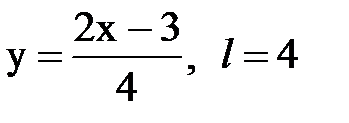 | 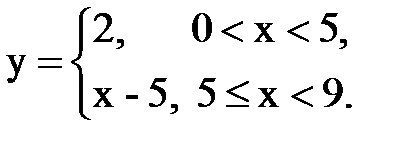 |
| 28. | 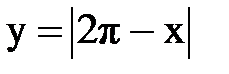 | 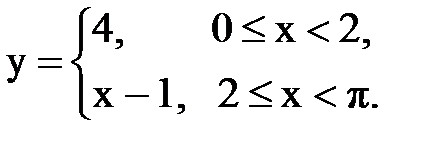 | 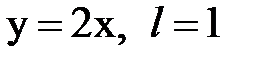 |
| 29. | 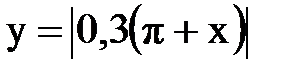 | 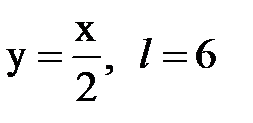 | 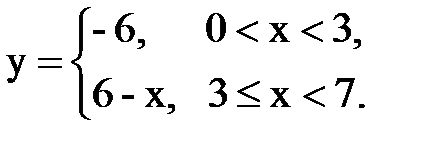 |
| 30. | 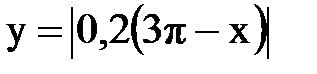 | 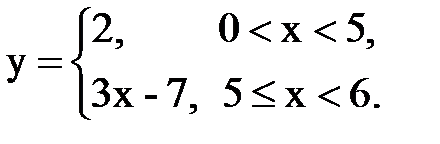 | 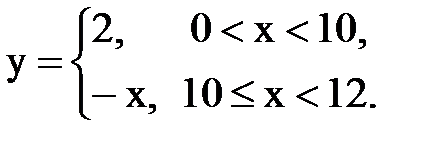 |
Справочный материал
Правила и формулы дифференцирования
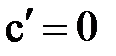 | 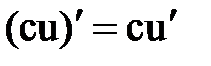 | 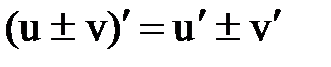 | 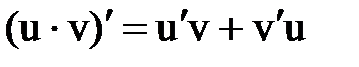 |
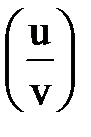 ¢ ¢ 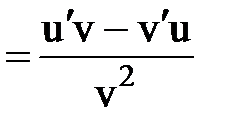 | 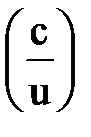 ¢ ¢ 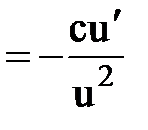 | 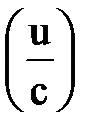 ¢ ¢ 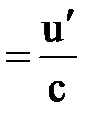 | 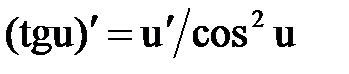 |
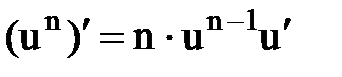 | 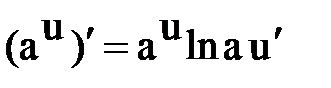 | 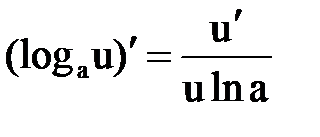  | 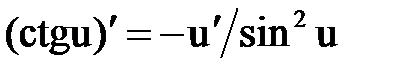 |
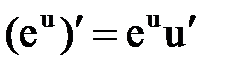 | 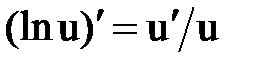 | 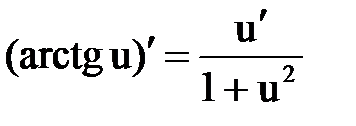 | 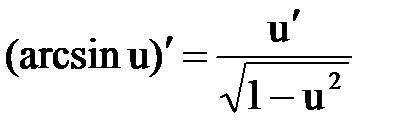 |
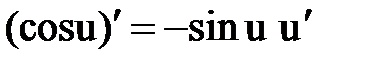 | 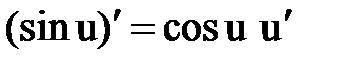 | 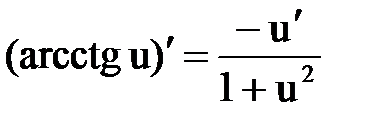 | 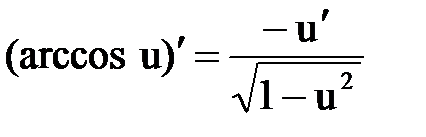 |
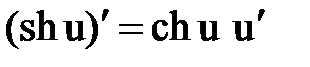 | 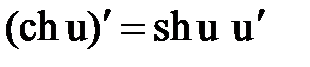 | 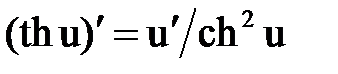 | 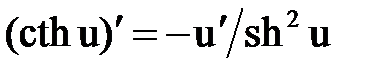 |
Интегрирование. Основные формулы и свойства
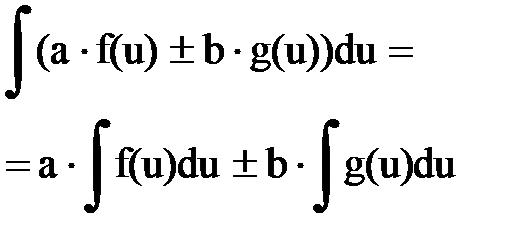 | 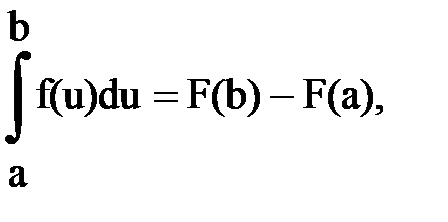 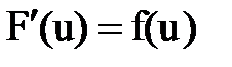 | ||||
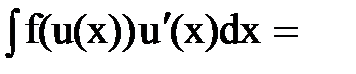 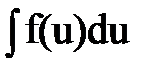 | 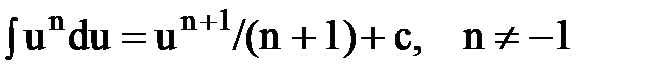 | ||||
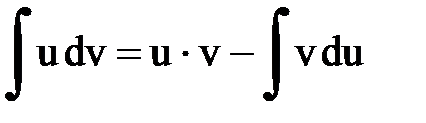 | 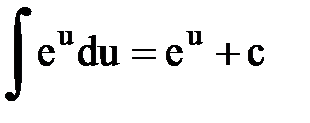 | 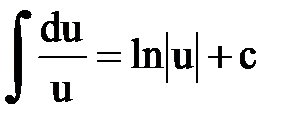 | |||
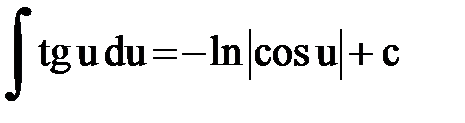 | 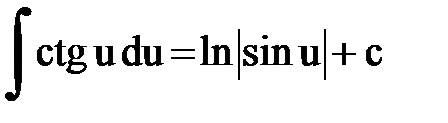 | ||||
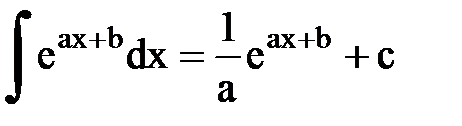 | 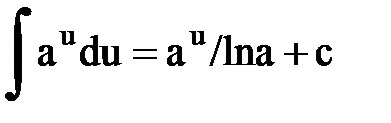 , a>0, a≠1 , a>0, a≠1 | ||||
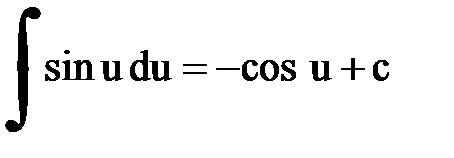 | 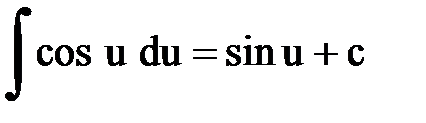 | 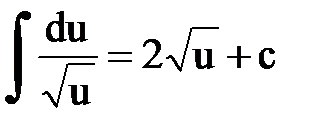 | |||
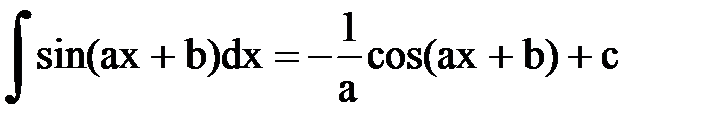 | 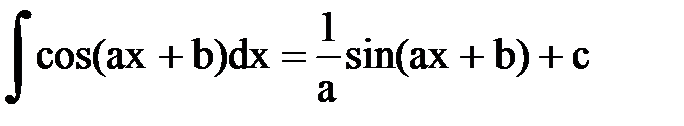 | ||||
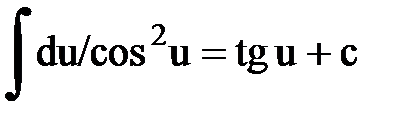 | 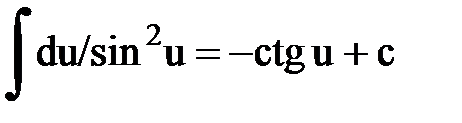 | 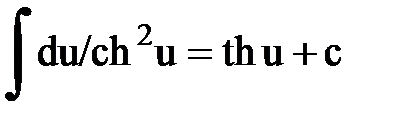 | |||
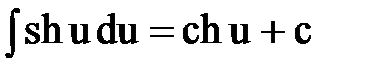 | 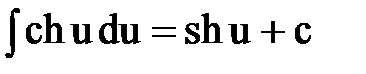 | 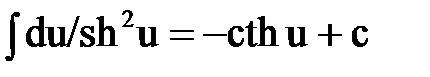 | |||
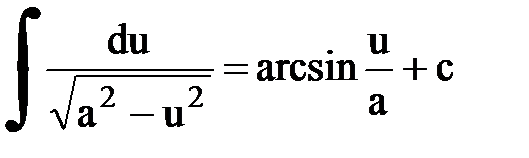 | 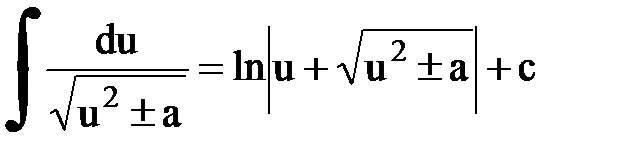 | ||||
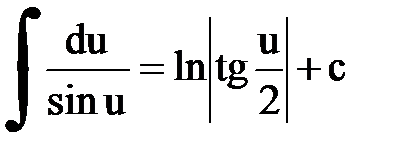 | 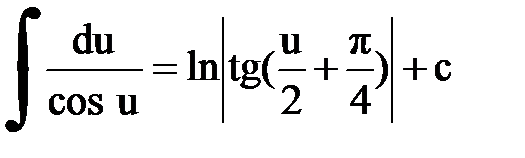 | 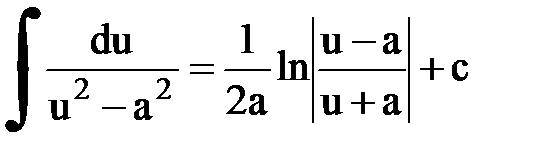 | |||
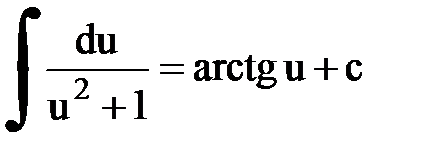 | 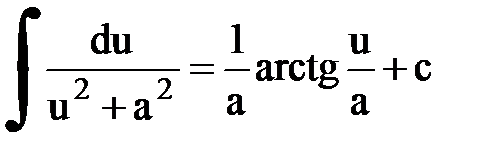 | ||||
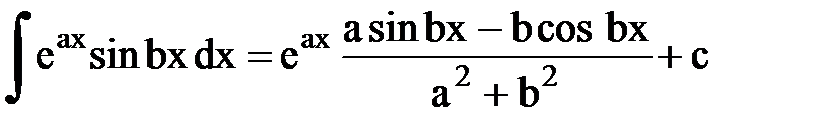 | 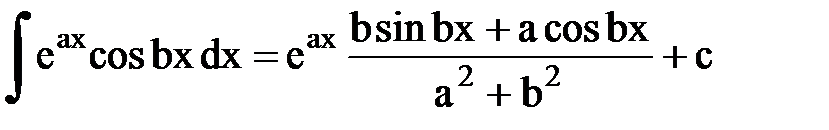 | ||||
Числовые и степенные ряды
Определение.Пусть дана бесконечная числовая последовательность {an}, сумма вида а1 + а2 + а3 + …+ аn +… называется числовым рядом и обозначается
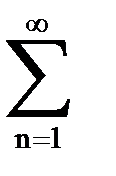 аn, (1)
аn, (1)
an называется n–м или общим членом ряда.
Определение.Сумма Sn= а1 + а2 + а3 + …+ аn n первых членов ряда называется n–й частичной суммой ряда.
Определение.Если существует конечный предел 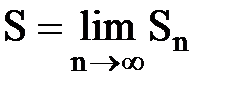 , то ряд называется сходящимся, а число S – суммой ряда. В этом случае пишут
, то ряд называется сходящимся, а число S – суммой ряда. В этом случае пишут 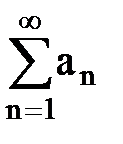 = S.
= S.
Определение.Ряд называется расходящимся, если 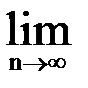 Sn не существует (в частности , если
Sn не существует (в частности , если 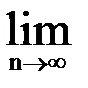 Sn = ¥).
Sn = ¥).
Справедливы следующие теоремы.
1. Отбрасывание от ряда или присоединение к нему любого конечного числа начальных членов не изменит его сходимости или расходимости.
2. Если все члены сходящегося ряда (1) умножить на число a, то получится сходящийся ряд 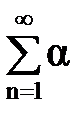 аn , а его суммой будет число aS.
аn , а его суммой будет число aS.
3. (Необходимый признак сходимости ряда.)Если ряд (1) сходится, то
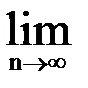 аn = 0. (Значит, если
аn = 0. (Значит, если 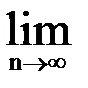 аn ≠ 0, то ряд(1) расходится.)
аn ≠ 0, то ряд(1) расходится.)
Действия над рядами
Теорема1.Если сходятся слагаемые ряды, то сходится и суммарный ряд:

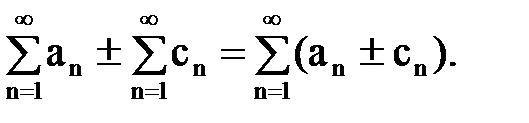
Теорема 2. Если сходятся перемножаемые ряды, причем хотя бы один абсолютно, то сходится и ряд 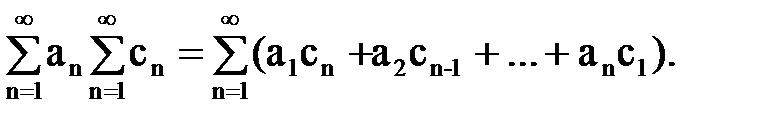
Определение.Частным от деления ряда 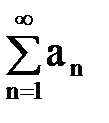 на ряд
на ряд 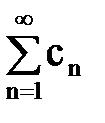 называется такой ряд
называется такой ряд 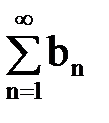 , что
, что 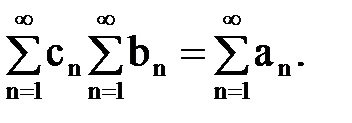
Степенные ряды
Определение. Степенным рядом называется функциональный ряд
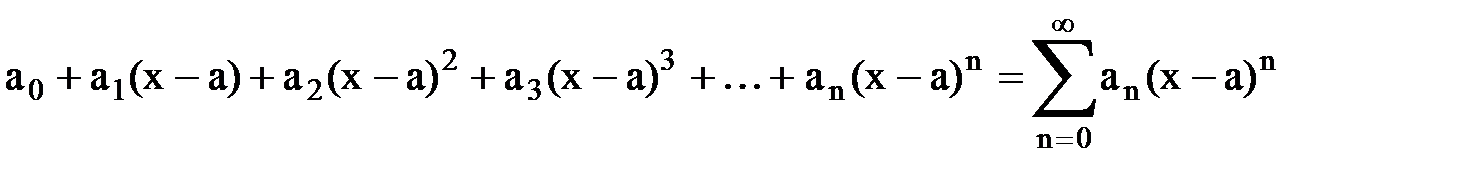 , (8)
, (8)
члены которого есть произведения постоянных 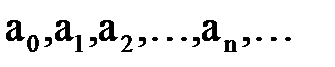 на степенные функции с целыми показателями степеней от разности (х - а).
на степенные функции с целыми показателями степеней от разности (х - а).
Постоянные а0, а1, а2, а3, …, аn, … называются коэффициентами степенного ряда. В частном случае при а = 0 имеют степенной ряд вида
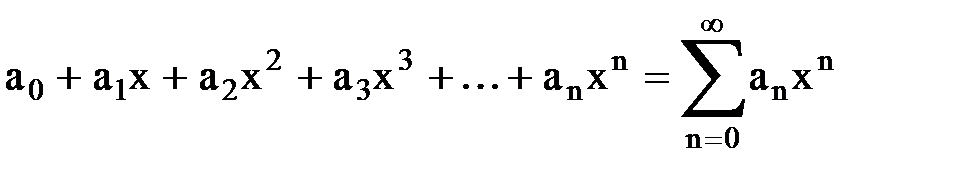 .
.
Основное свойство степенных рядов сформулировано в теореме Абеля. Если степенной ряд (8) сходится при х = х0, то он сходится и притом абсолютно при всяком значении х, удовлетворяющем условию
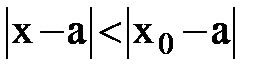 .
.
Одним из следствий теоремы Абеля является существование для всякого степенного ряда интервала сходимости, симметричного относительно х = а [для ряда (8)]. Обозначим через число R половину длины интервала сходимости – радиус сходимости. Тогда интервал сходимости для ряда (8) запишется в виде
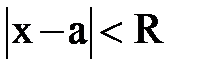 или
или 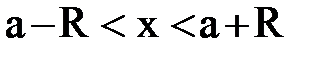 ,
,
а при а = 0
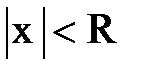 или
или 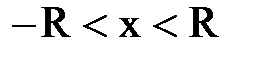 .
.
В частных случаях радиус сходимости ряда R может оказаться равным нулю или бесконечности. Если R = 0, это озна
