Зарождение и история развития систем счисления.

Лабораторная работа №2

Системы счисления

Представление чисел с фиксированной и плавающей запятой

При представлении числа в двоичном коде с цифрами 0,1 в каждом разряде записываются цифры 0 или 1. Так как в ЭВМ «запись» числа осуществляется с помощью технических устройств, то для представления его в такой форме необходимо располагать устройствами с двумя надежно различными состояниями, которым могут быть сопоставлены значения 0 или 1. Комбинация таких устройств, число которых соответствует количеству разрядов записываемого числа, может быть использована для представления чисел в ЭВМ.

В качестве таких устройств, могут быть использованы триггеры. Набор триггеров, предназначенных для представления чисел в ЭВМ, а также для выполнения над ними некоторых логических преобразований, называется регистром. Разумеется, число разрядов, отведенное для записи числа, соответствующее числу триггеров, в ЭВМ всегда конечно. Выбор количества разрядов для представления чисел в ЭВМ является одним из самых ответственных этапов конструирования вычислительной машины и обуславливается целым рядом требований, среди которых одно из важнейших – необходимая точность вычислений.

В ЭВМ применяются две основные формы представления чисел: с плавающей запятой и с фиксированным положением запятой. При представлении чисел с фиксированной запятой положение запятой закрепляется в определенном месте относительно разрядов числа и сохраняется неизменным для всех чисел, изображаемых в данной разрядной сетке. Обычно запятая фиксируется перед старшим разрядом или после младшего. В первом случае в разрядной сетке могут быть представлены только числа, которые по модулю меньше 1, во втором – только целые числа.

Использование представления чисел с фиксированной запятой позволяет упростить схемы машины, повысить ее быстродействие, но представляет определенные трудности при программировании. В настоящее время представление чисел с фиксированной запятой используется как основное только в микроконтроллерах. В универсальных ЭВМ основным является представление чисел с плавающей запятой. Широкий диапазон представления чисел с плавающей запятой удобен для научных и инженерных расчетов. Для повышения точности вычислений во многих ЭВМ предусмотрена возможность использования формата двойной длины, однако при этом происходит увеличение затрат памяти на хранение данных и замедляются вычисления.

Перевод целых чисел из одной позиционной системы счисления в другую

Перевод целых чисел из десятичной системы счисления в любую другую

Правило перевода чисел: для перевода числа из одной позиционной системы в другую нужно делить число на основание новой системы счисления, затем частное от деления тоже делить на основание новой системы до тех пор, пока оно не станет меньше основания новой системы счисления. Выписав последнее частное и все остатки, начиная с последнего, получим представление этого числа в новой системе счисления.

Пример. Число А=172₁₀ перевести в двоичную, восьмеричную и шестнадцатеричную системы счисления.

1. А=172₁₀ ® А₂

172 ë2_

172 86 ë2_

0 86 43 ë2_

ã 0 42 21 ë2_

ã 1 20 10 ë2_

ã 1 10 5 ë2_

ã 0 4 2 ë2_

ã 1 2 1

ã 0 å

172₁₀ = 10101100₂.

A₁₀ = 172, A₈ =? A₁₀ = 172, A₁₆ =?

172 ë8_ 172 ë16_

168 21 ë8_ 160 10 (=A)

4 16 2 (C=) 12 å

ã 5 å

172₁₀ = 254₈ 172₁₀ = AC₁₆

Перевод чисел из любой позиционной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную достаточно вспомнить формулу записи числа в позиционной системе счисления.

N= a m*q m+a m-1*q m-1+ a m-2*q m-2++ a 1*q 1+ a 0*q 0+ a -1*q -1+ a -2*q -2+…+ a-s*q –s

Данная формула позволяет найти значение числа в десятичной системе счисления. Чтобы выполнить такой перевод, нужно над всеми цифрами числа, начиная с последней, написать соответствующие степени, а затем найти сумму произведения каждой цифры числа на основании исходной системы счисления в данной степени.

Например, нам нужно перевести число из пятеричной системы счисления в десятичную систему:

_{4 3 2 1 0 -1 -2}

43224,31₅=4*5⁴+3*5³+2*5²+2*5¹+4*5⁰+3*5^-+1*5²=2500+375+50+10+4+3/5+1/25= 2979,64₁₀

_{9 8 7 6 5 4 3 2 1 0}

1020210121₃=1*3⁹+0*3⁸+2*3⁷+0*3⁶+2*3⁵+1*3⁴+0*3³+1*3²+2*3¹+1*3⁰==19683+4374+486+81+9+6+1=24640₁₀

Примеры:

100111011₂=1*2⁸+1*2⁵+1*2⁴+1*2³+1*2¹+1*2⁰

34567₈=3*8⁴+4*8³+5*8²+6*8¹+7*8⁰

5214233₆ =5*6⁶+2*6⁵+1*6⁴+4*6³+3*6²+3*6¹+3*6⁰

98D4A2C3₁₆ =9*16⁷+8*16⁶+13*16⁵+4*16⁴+10*16³+2*16²+12*16¹+3*16⁰

Разбор заданий

Дана правильная дробь 29/32. Представьте ее в двоичной системе счисления.

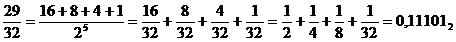Дана дробь 60/64. Перевести ее в восьмеричную и шестнадцатеричную системы счисления:

а) Переведем дробь в двоичную систему счисления

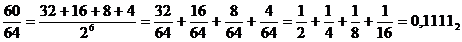б) Переведем дробь в восьмеричную систему счисления путем разбиения двоичного числа на триады:

0,111 1002=0,748

в) Переведем дробь в шестнадцатеричную систему счисления путем разбиения двоичного числа на тетрады: 0,1111 2=0,F16

Разбор заданий

Сложить два числа в двоичной системе счисления А и В.

А=1101001; В=1011101111

₊ 1011101111

1101011000

Проверим правильность сложения: вычтем из суммы А и В число В.

_1101011000

1011101111

3. Найти сумму чисел А и В в восьмеричной системе счисления

А=56744₈; В=2765₈

₊ 56744

2765

4.Проверим правильность сложения: вычтем из суммы А и В число В.

_ 61731

2765

56744₈

5. Найти сумму чисел А и В в шестнадцатеричной системе счисления

А=960А74₁₆; В=В7685Е₁₆

₊96 0А74₁₆

В7685Е₁₆

14D72D2₁₆

6.Проверим правильность сложения: вычтем из суммы А и В число В.

_14D72D2₁₆

В7685Е₁₆

960A74₁₆

Лабораторная работа №2

Системы счисления

Зарождение и история развития систем счисления.

На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Это был еще не счет, а лишь его зародыш. Впоследствии способность различать друг от друга небольшие совокупности развивалась: возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество.

С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах. Для этого человек пользовался окружавшими его предметами, как инструментами счета: он делал зарубки на палках и на деревьях, завязывал узлы на веревках, складывал камешки в кучки и т.п. Это удобно, так как сразу визуально определяется количество знаков и сопоставляется с количеством предметов, которые эти знаки обозначают. Счёт на счетных палочках в первом классе – это отзвук той далекой эпохи. Кстати, от счета с помощью камешков ведут свое начало различные усовершенствованные инструменты, как, например, русские счеты, китайские счеты («сван-пан»), древнеегипетский «абак» (доска, разделенная на полосы, куда клались жетоны). Аналогичные инструменты существовали у многих народов. Более того, в латинском языке понятие «счет» выражается словом «calculatio» (отсюда наше слово «калькуляция»); а происходит оно от слова «calculus», означающего «камешек».

Особо важную роль играл природный инструмент человека – его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был «под рукой» и отличался большой подвижностью. Язык первобытного человека был беден; жесты возмещали недостаток слов, и числа, для которых еще не было названий, «показывались» на пальцах.

Поэтому, вполне естественно, что вновь возникавшие названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках; у некоторых народов возникали также названия чисел на основе числа 5 – по количеству пальцев на одной руке или на основе числа 20 – по количеству пальцев на руках и ногах.

На первых порах расширение запаса чисел происходило медленно. Сначала люди овладели счетом в пределах нескольких десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества. В русском языке слово «сороконожка» имеет смысл «многоножка»; выражение «сорок сороков» означало в старину число, превосходящее всякое воображение.

На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово «сто» приобретает смысл неопределенно большого числа. Такой же смысл приобретают потом последовательно числа тысяча, десять тысяч (в старину это число называлось «тьма»), миллион.

На современном этапе границы счета определены термином «бесконечность», который не обозначает, какое либо конкретное число. В современном русском языке, а также в языках других народов названия всех чисел до миллиона составляются из 37 слов, обозначающих числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 , 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например, восемьсот пятнадцать тысяч триста девяносто четыре). В свою очередь названия этих 37 чисел, как правило, образованы из названий чисел первого десятка (1, 2, 3, 4, 5, 6, 7, 8, 9) и чисел 10, 100, 1000 (например, 18 = восемь на десять, 30 = тридесять и т.д.). В основе этого словообразования лежит число десять, и поэтому наша система наименований называется десятичной системой счисления. Из упомянутого правила в разных языках имеются различные исключения, объясняющиеся историческими особенностями развития счета. В русском языке единственным исключением является наименование «сорок». Это исключение можно поставить в связь с тем, что число 40 играло некогда особую роль, означая неопределенно большое количество. В тюркских языках (узбекском, казахском, татарском, башкирском, турецком и др.) исключение составляют наименования чисел 20, 30, 40, 50, тогда как названия чисел 60, 70, 80, 90 образованы из наименований для 6, 7, 8, 9. Во французском языке сохранились недесятичные названия чисел 20 и 80, причем 80 именуется quatrevingt, т.е. «четыре двадцать». Здесь мы имеем остаток древнего двадцатеричного счисления (по числу пальцев на руках и ногах). В латинском языке наименование числа 20 тоже недесятичное (viginti). Наименования чисел 18 и 19 образованы из названия 20 с помощью вычитания: 20–2 и 20–1 (duodeviginti, undeviginti, т.е. «два от двадцати», «один от двадцати»).