Экспоненциальные кривые роста

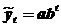- простая экспонента;

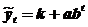- модифицированная экспонента,

где а,0 < b < 1 – постоянные числа; k = const – асимптота функции.

Для простой экспоненты:

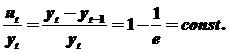
Экспоненту можно преобразовать в линейную зависимость посредством логарифмирования:

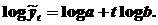
3. S-образные кривые роста характеризуют процессы, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому – либо пределу, например, ввод некоторого объекта в промышленную эксплуатацию. Среди S-образных кривых роста наиболее известна кривая Гомперца:

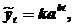
где a, 0 < b < 1 – положительные параметры; k – асимптота.

Кроме того, часто используется логистическая кривая (кривая Перла-Рида):

,

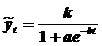где a, b – положительные параметры; k – асимптота.

Конфигурация графика логистической кривой близка к графику кривой Гомперца, т.е. напоминает букву S, но в отличии от последней логистическая кривая имеет точку симметрии, совпадающую с точкой изгиба.

Для выбора вида полиноминальной кривой роста рекомендуется метод конечных разностей (метод Титнера), если уровни ВР состоят только из тренда и случайной компоненты, причём тренд является достаточно гладким.

1. Вычисляются разности до k – го порядка (обычно до 4 – го порядка)

……………….

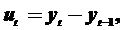
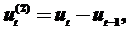
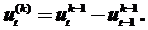
2. Вычисляются дисперсии для ВР и для каждого разностного ряда. Для ВР по формуле:

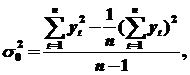
а для разностного ряда k -го порядка (k = 1, 2, …) по формуле:

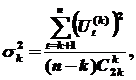
где 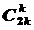– биноминальный коэффициент (число сочетаний).

3. Вычисляются величины

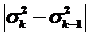
до тех пор, что при каком -то значении k будет выполняться неравенство

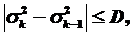
где D – заданное число.

В этом случае степень аппроксимирующего полинома должна быть равна (k – 1).

Более универсальным является метод характеристик прироста, который до этого сглаживается методом простой скользящей средней с интервалом m=3. В этом случае уровни рассчитываются по формуле:

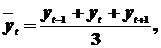
а первый и последний уровни по формулам:

Затем вычисляются первые средние приросты:

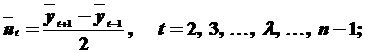
вторые средние приросты:

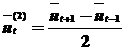
и ряд производных величин:

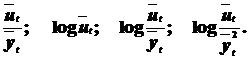
В соответствии с полученными результатами делается выбор вида кривой роста для исходного ВР по таблице (таблица 7.4).

Таблица 7.4

Выбор вида кривой роста

Показатель	Характер изменения показателя во времени	Вид кривой роста
Первый средний прирост	Примерно одинаковы	Полином первого порядка (прямая)
Первый средний прирост	Изменяются линейно	Полином второго порядка (парабола)
Второй средний прирост	Изменяются линейно	Полином третьего порядка (кубическая парабола)
	Примерно одинаковы	Простая экспонента
	Изменяются линейно	Модифицированная экспонента
	Изменяются линейно	Кривая Гомперца
	Изменяются линейно	Логистическая кривая