Методы выявления тренда во ВР

Основными методами для определения тренда являются:

Метод проверки разностей средних уровней, который реализуется поэтапно.

а) ВР y₁, y₂, ..., y_n разбивается на две примерно равные по числу уровней части n₁ и n₂ (n₁+n₂=n);

б) для каждой части вычисляются средние значения 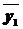и , и 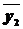дисперсии D₁=σ₁², D₂=σ₂² (см. метод Ирвина);

в) проверяется равенство (однородности) дисперсий обеих частей ряда с помощью F – критерия Фишера

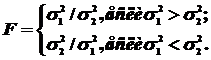
Расчетное значение критерия F сравнивается с табличным (критическим) значением F_α с заданным уровнем значимости (уровнем ошибки) α. В качестве α чаще всего берут значения α=0,1 (10%-я ошибка) , α=0,05 и α=0,01. Величина (1–α) называется доверительной вероятностью.

Если расчетное значение F < F_α, то гипотеза об однородности дисперсий принимается и переходят к следующему этапу. Если F F_α , то гипотеза об однородности дисперсий отклоняется, т.е. данный метод для определения наличия тренда ответа не дает;

г) проверяется гипотеза об отсутствии тренда с использованием t-критерия Стьюдента. Для этого определяется расчетное значение критерия:

,

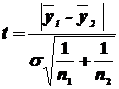где 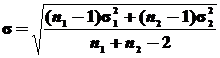– среднее квадратическое отклонение разности средних.

Если t < t_α с заданным уровнем значимости α, то гипотеза принимается (тренда нет), где t_α – табличное значение, которое берется для числа степеней свободы, равного n₁+n₂–2. Если t > t_α, то тренд есть. Метод применим для рядов с монотонной тенденцией.

Метод Фостера-Стьюарта обладает большими возможностями и дает более надежные результаты, которые позволяют установить наличие тренда не только для средних значений, но и для тренда дисперсии (если дисперсия увеличивается, то ряд «раскачивается»).

а) производится сравнение каждого уровня исходного ВР, начиная с y₂ , со всеми предыдущими и определяются две числовые последовательности:

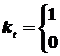, если y_t больше всех предыдущих уровней;

, в противном случае.

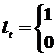, если y_t меньше всех предыдущих уровней;

, в противном случае,

где t = 2,3,…,n;

б) вычисляются величины s и d:

;

.

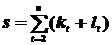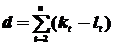Если s = 0, то уровни ряда равны между собой, а если s=n–1, то ряд монотонный. Величина d характеризует изменение дисперсии при крайних значениях d=- (n–1) – ряд монотонно убывает; d=n–1 – ряд монотонно возрастает.

в) проверяются гипотезы: можно ли считать случайными:

1) отклонение величины s от величины μ– математического ожидания величины s для ряда, в котором уровни расположены случайным образом;

2) отклонение величины d от нуля.

Проверка проводится по t-критерию Стьюдента для средней и для дисперсии:

;

;

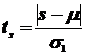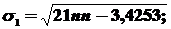
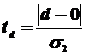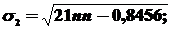
где σ₁, σ₂ – среднеквадратические отклонения для величин s и d соответственно.

Значения μ, σ₁, σ₂ иногда табулируются. В таблице представлен фрагмент табулированных значений величин μ, σ₁, σ₂.

Таблица 7.2

Табулированные значения μ, σ₁, σ₂

n
μ	3,858	5,195	5,990	6,557
σ1	1,288	1,677	1,882	2,019
σ2	1,964	2,279	2,447	2,561

г) сравниваются расчетные значения t_s и t_d с табличными t_α с заданным уровнем значимости; если t_s<t_α и t_d<t_α , то тренды в среднем и у дисперсии отсутствуют; если t_s>t_α и t_d<t_α , то имеется тренд в среднем, а тренда у дисперсии ряда – нет и т.д.; t-критерий Стьюдента выбирается из условия α и (n–1).

Методы сглаживания ВР

Очень часто уровни экономических рядов динамики колеблются и тенденция развития экономического явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. Чтобы более четко обозначить тенденцию развития процесса, производят сглаживание (выравнивание) ВР.

Различают аналитическое выравнивание с помощью известных уравнений различных линий (прямая, экспонента и.т.д.) и механическое выравнивание ВР с использованием фактических значений соседних уровней.

При механическом сглаживании берется несколько первых уровней ВР (интервал сглаживания). Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания. С помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо и вычисляется второе сглаженное значение и.т.д.

Метод простой скользящий средней. Интервал по возможности берут большим и состоящим из нечетного числа уровней. Для первых m уровней, образующих интервал сглаживания, вычисляют среднее арифметическое значение, которое соответствует середине интервала:

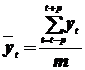; t > p; 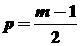(m – нечетно).

Далее делается сдвиг на один уровень вправо и операция повторяется.

В результате такой процедуры получаются n–m+1 сглаженных значений уровней ряда. При этом первые и последующие p уровней теряются (не сглаживаются). Рекомендуется только для рядов, имеющих линейную тенденцию.

В методе взвешенной скользящей средней уровни, входящие в интервал сглаживания, суммируются с разными весами, т.к. для сглаживания используются полиномы второй и большей степени.

Средняя арифметическая взвешенная определяется как:

,

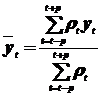где ρ_t – веса, определяемые методом наименьших квадратов.

Особенностью метода экспоненциального сглаживания является то, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда.

Сглаженные значения уровней S_t , t=1,2,…,n определяются по формуле:

S_t = αy_t + (1–α)S_t-1,

где α – параметр сглаживания (0<α<1);

(1–α) – коэффициент дисконтирования.

Сглаженное данным методом значение уровня ряда является взвешенной средней всех предшествующих уровней:

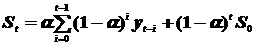
где S₀ – величина, характеризующая начальные условия; рекомендуются выбирать S₀=y₁ или S₀=1/3(y₁+y₂+y₃).

Значение α рекомендуется выбирать в пределах 0,1 0,3. Р.Браун предлагает выбирать α, исходя из данных ряда:

.

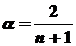Если при подходе к правому концу ВР, сглаженные этим методом значения при выбранном параметре α начинают значительно отличаться от соответствующих значений исходного ряда, то необходимо перейти на другой параметр сглаживания.

При этом методе не теряются ни конечные, ни начальные уровни ВР.

Оценка автокорреляции во ВР

Часто возникает необходимость оценить зависимость изучаемого показателя y_t от его значений, рассматриваемых с некоторым запаздыванием во времени. Зависимость значений уровней ВР от предыдущих (сдвиг на 1), предпредыдущих (сдвиг на 2) и.т.д. уровней того же ВР называется автокорреляцией во ВР.

Автокорреляционная функция вычисляет взаимную корреляционную функцию между исходным рядом y_t и этим же рядом, сдвинутым во времени на величину τ.

.

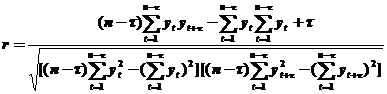Задавая различные значения τ=1,2,3,… (сдвиг) получают значения r₁, r₂, r₃,… и т.д. На практике рекомендуется вычислять такие коэффициенты в количестве от n/4 до n/3.

График автокорреляционной функции называется кореллограммом и показывает величину запаздывания, с которым изменение показателя y_t сказывается на его последующих значениях. Величина сдвига τ, которому соответствует наибольший коэффициент автокорреляции, называется временным лагом.

Иногда используется упрощенная формула:

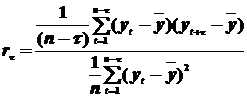
где 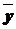– средний уровень ряда.

Пример 7.2. Найти коэффициент автокорреляции r_τ ВР для разных значений лага на основании 10-ти наблюдений, представленных стационарным рядом:

y_t = (421;392;403;350;364;406;418;382;318;354).

Определяем среднее арифметическое членов ВР:

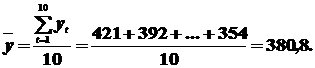
Подсчитывая значение коэффициента автокорреляции для следующих значений лага τ=1,2,…,5. Для этого составим таблицу.

Таблица 7.3