Прямая геодезическая задача.
Существуют две основные задачи геодезии, которые применяются во всех трех отраслях этой науки. Это определение координат на местности и углов ориентирования аналитическим методом. Прямая геодезическая задача предполагает определение координат одной искомой точки, когда известны координаты одной заданной точки. При этом дирекционный угол и длина соединяющей эти точки линии должны быть известны. (Рис.3). Каждый изучающий геодезию должен усвоить решение этих задач.
 |  | ||||||
 |  | ||||||
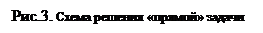
Итак, выводим формулы прямой геодезической задачи.
Дано: координаты точки А: уА, хА.
дирекционный угол линии aАВ (альфа) АВ
длина линии АВ-d АВ
Определить: координаты точки В: уВ, хВ.
Решение: Обращаемся к прямоугольному треугольнику АDB, у которого известен один угол a и гипотенуза АВ-d АВ. Из чертежа (рис.3) следует, что искомые координаты:
уВ = уА + Dу, хВ = хА +Dх (1), где неизвестными являются Dу и Dх, найдя которых, мы решим задачи. Из тригонометрии известно, что противолежащий к известному углу катет прямоугольного треугольника равен DB = Dу = d АВ * Sin a (2), а прилежащий к углу катет равен АD = Dх = d АВ * Сos a (3). Таким образом, подставляя формулы (2), (3) в формулу (1) получаем: уВ = уА + d АВ * Sin a; хВ = хА + d АВ * Cos a.
Обратная геодезическая задача.
Обратная геодезическая задача в основном применяется в инженерной геодезии для выноса проектированного на плане объекта на местность. При этом координаты исходной точки и точек объекта должны быть известны и через них можно узнать как ориентирован объект и на каком расстоянии относительно исходных точек находится.
Итак, выводим формулы обратной геодезической задачи. (Рис.3)
Дано: уА, хА, уВ, хВ
Определить: a АВ, d АВ.
Обращаемся к прямоугольному треугольнику ADB. Так как координаты известны, определяем их разность - приращение координат Dу, Dх и через них находим дирекционный угол - a АВ. Из тригонометрии известно, что тангенс угла равен отношению противолежащего катета к прилежащему.
Dy = yВ - y А tga =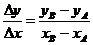 
Отсюда находим угол: a= arctg a
Dx = хВ - х А
Длину d можно найти по формуле Пифагора
2 2 2 2
dАВ =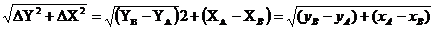 
Для контроля длину можно найти еще по двум формулам, решая через (2) и (3).
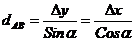
Эти формулы являются контрольными. Совпадение результатов зависит от правильности нахождения a АВ.
Теодолитные ходы.
Есть разные методы определения координат точек местности. Есть высокоточные методы, называемые триангуляция, полигонометрия, которые применяются для составления точных карт. Есть менее точный метод, называемый теодолитные ходы, который применяется для составления плана (горизонтальные проекции) малого участка земли. План составляется для проектирования различных объектов, может быть составлен кем угодно, но для этого надо владеть элементарными знаниями по прокладке и вычислению теодолитных ходов, по пользованию геодезическим прибором - теодолит и по методике производства съемки участка местности.
Берется участок местности, на котором необходимо спроектировать и построить небольшие объекты. Необходимо для проектирования иметь план участка в каком-либо масштабе. Для создания плана надо выполнить съемку участка. Для этого создается сеть так называемых опорных точек. Опорная точка, это точка местности, отмеченная на земле чем-либо, например, металлическим штырем или деревянным колышем. Местоположение опорной точки должно быть известно не только на местности, но на плане. Для этого определяют их координаты. Одним из методов определения прямоугольных координат являются теодолитные ходы. Теодолитные ходы состоят из опорных точек, взаимосвязанных друг с другом, расстояние между которыми разрешается от 60 м до 250 м. Теодолитные ходы могут иметь форму замкнутого многоугольника, если участок имеет примерно округлую форму. Теодолитные ходы будут иметь форму вытянутой ломаной линии, если участок работ - вытянутый.
Необходимым условием определения координат точно как при решении прямой геодезической задачи, является наличие исходной опорной точки с заранее известными координатами. Такими исходными точками могут быть опорные точки, у которых координаты определены другими более точными методами, как триангуляция и полигонометрия.
Порядок работ при прокладке теодолитных ходов следующий:
1. Обход участка будущих работ;
2. Измерение горизонтальных углов теодолитом;
3. Измерение длин между точками теодолитного хода рулеткой или мерной лентой;
4. Проверка правильности угловых измерений путем вычисления невязки (неувязки);
5. Вычисление дирекционных углов;
6. Вычисление приращений координат и их невязок;
7. Вычисление координат и построение плана по координатам в заданном масштабе.
Основное вычисление выполняется по формуле прямой геодезической задачи (см.) Остальные измерения и вычисления диктуются необходимостью определения параметров этой задачи.
Основная формула для определения дирекционного угла последующей линии получается по чертежу. При этом начальный дирекционный угол должен быть известным. (Рис. 4) a6 = a1 + 180° - b
|
|
 | |||
 | |||
ю
Ю
Рис. 4
Топографическая съемка.
Слово «топо» в переводе с латинского означает поверхность. В данном случае поверхность земли. «Граф» - означает чертеж. Наиболее доступным чертежом местности является его план, составленный в каком-либо масштабе. Масштаб - это отношение отрезка на плане, равного одному сантиметру к величине этого отрезка на местности в сантиметрах. Например: один сантиметр на плане или на карте равен 500 сантиметрам местности, следовательно, пишем масштаб (его принято писать в виде дроби) 1:500. Если 1 см. На плане равен 10 метрам на местности, то пишем 1:1000, что можно расшифровать так: 1 см. на плане равен 1000 см. на местности.
Для составления плана местности необходимо выполнить топографическую съемку местности. Съемка геодезическими приборами существенно отличается от фотосъемки. Съемки выполняются через геодезические измерения относительно опорных точек. При этом снимаемый объект разлагается на характерные точки. Например, если снимается здание, то характерными точками будут углы здания. Определив положение углов зданий относительно опорных точек каким-либо способом, можем построить план здания, соединив линиями его угловые точки.
Существуют следующие виды топографических съемок:
1. Тахеометрическая
2. Мензульная
3. Аэрофотогеодезическая
Мы остановимся на тахеометрической съемке. Слово «тахео» в переводе с греческого означает - быстро. Следовательно, в буквальном переводе получается быстроизмерительная съемка. Измерения на местности выполняются быстро, например, в летнее время. А план можно чертить не спеша зимой. Во время съемки рисуется абрис снимаемой местности, на котором показывается какая точка где находится и что обозначает: угол здания, угол леса, перекресток дорог, столб и т.д. Абрис не имеет масштаба.
При тахеометрической съемке попутно определяются высоты (отметки) точек местности от уровня моря. Для этого необходимы дополнительные геодезические работы. Высотные работы в геодезии называются нивелированием. Существуют три вида тахеометрической съемки: 1. Полярный метод. 2. Метод перпендикуляров (метод ординат). 3. Метод угловых и линейных засечек. При полярном методе съемки, положение снимаемой точки определяются через угол и длину линии, т.е. определяются полярные координаты. Причем центром полярных координат является опорная точка, над которой стоит теодолит. Ее называют обычно станцией. Осью полярных координат является линия между опорными точками. (Рис.5)
Рис.5. Схема съемок полярным методом и методом ординат.
При любой топографической съемке одновременно с объектами снимается и рельеф (неровности) местности. Для этого определяется высота от уровня моря (отметка) каждой снимаемой точки. Отметки опорных точек определяются заранее.
Относительно опорных точек (станций) находят превышение - разность высот станции и снимаемой точки. Превышение определяется тригонометрическим нивелированием, формула которого получается из чертежа. (рис.6)
Рис.6. Схема тригонометрического нивелирования.
HCT - высотная отметка станции, заранее известна;
HN – высотная отметка снимаемой точки, где стоит рейка;
h – “превышение” (если искомая точка ниже, чем станция, то оно будет отрицательным).
i – высота прибора;
L – высота наведения;
V – угол наклона (измеряется вертикальным кругом теодолита);
I
Д - наклонное расстояние между точками;
d – горизонтальное проложение – проекция измеренной длины на горизонтальную плоскость. Итак отметка равна:
HN = HCT + h,
h – определяется через другие измеренные параметры. Из чертежа видно, что
h = h¢ + i – L,
где i и L – измерены, а получается по формуле тригонометрии:
h¢ = d * tgv, где
d = D¢ * Cosv
Если L = i, т.е. на рейке сделана метка для наведения на уровне высоты прибора, то h = h¢ = dtgv
А угол наклона измеряется вертикальным кругом теодолита при круге право (К.П.) и при круге лево (К.Л.) или только при К.Л.
После окончания всех вычислений, вычерчивается план, на котором строятся и объекты и рельеф. Рельеф показывается горизонталями.
В данном случае горизонталью называется линия, проходящая через точки с одинаковыми высотами (отметками) от уровня моря. Одна линия горизонтали показывает, где проходит на земле одинаковый уровень на какой-либо одной высоте от уровня моря, например, на высоте 130 м. Форма горизонтали повторяет форму рельефа на данном уровне. Для вычерчивания одной горизонтали необходимо искать точки с одинаковой высотой, например, 130 м. И плавно соединить их одной линией. Высоты горизонтальной кратны высоте сечения горизонталей. Высота сечения показывает через какой отрезок по вертикали мы решили мысленно рассекать землю горизонталями.
Заложением называется расстояние между смежными горизонталями. Его величина зависит от величины уклона местности. Чем больше уклон, тем меньше заложение. Уклон зависит от наклона участка земли на данном направлении. В строительной практике принято определять уклон какого-либо направления местности без измерения угла наклона. Обычно за уклон принимают отношение разности высот двух точек земли к величине горизонтального положения между ними. (рис.7.)
рис.7. Схема для определения уклона местности
Таким образом, уклон: 
Знак уклона зависит от знака превышения (разности высот).
На листе карты или плана обычно вычерчивают график заложений, где по вертикали откладывают отрезки между смежными горизонталями (величине заложений), а по горизонтали пишут соответствующие им уклоны или углы наклона на земле. Пользуясь этим графиком, можно найти средний уклон местности между какими-либо точками.
Если хорошо усвоите все выше сказанное, Вы легко выполните контрольную работу №1. Если будет что-либо непонятно по выполнению контрольной работы, просим еще раз прочитать и представить себе как происходят все действия на местности.
Контрольная работа №1.
Задание 1. Вычисление исходных дирекционных углов линий;