Система прямоугольных плоских координат в геодезии.
Введение
Геодезия – это наука об измерениях на земной поверхности, о приборах для их выполнения и методах математической обработки этих измерений. Измерения выполняются с целью определения координат и высот точек Земли, для производства съемок участков Земли, что в свою очередь необходимо для составления планов и карт.
Геодезия как наука делится на три отрасли: 1. Высшая геодезия; 2.Общая геодезия; 3. Инженерная или прикладная геодезия.
Высшая геодезия изучает высокоточные методы определения координат и высот, повторное определение которых дает установить степень изменения фигуры и размеров Земли во времени.
Общая геодезия изучает методы определения координат и высот точек Земли с целью их применения для производства съемок, методы составления планов и профилей местности по материалам этих съемок.
Инженерная или прикладная геодезия изучает методы применения геодезических измерений для решения различных инженерных задач. Примеров применения множество и зависит от того, как к какой области прикладывается геодезия: к строительству, прокладке коммуникаций, автодорог и т.д.
Большую пользу науке и производству дают периодически повторяющиеся геодезические замеры. например, высотные измерения связанные с определением вертикальных перемещений участков Земли и сооружений.
Система прямоугольных плоских координат в геодезии.
Для составления планов малых участков Земли достаточно знать систему координат Гаусса-Крюгера. Немецкие ученые Гаусс и Крюгер (19в.) предложили разделить Землю на отдельные зоны меридианами через 6°С по долготе, таким образом земной шар как какой-либо арбуз делится на дольки (60 зон). Берем корочку из каждой дольки и распрямляя кладем на стол. Таким образом получается совершенно плоская одна шестидесятая часть Земли, на которой средний меридиан и часть экватора получаются в виде прямых линий (рис.1)
рис.1
Пусть нас интересует северное полушарие. Гаусс предложил так: пусть средний меридиан зоны будет ось абсцисс (х), все х-сы на северном полушарии положительны, а линия экватора ось ординат (у). Так как Земля не плоскость, мы берем только одну какую-либо зону. Следовательно, в каждой зоне будет начало координат. Это означает, что на Земле будет 60 точек с совершенно одинаковыми координатами. А как тогда по прямоугольным координатам узнать где же на Земле она находится? Для уточнения необходимо узнать номер зоны. Зоны нумеруются начиная с нулевого меридиана (гринвического) к востоку.
Углы ориентирования.
Углами ориентирования называются углы от общепринятого направления ориентирования (север-юг) до какого-либо направления на местности. Угол ориентирования зависит от местонахождения начальной точки. Простым примером может служить следующее: Угол ориентирования направления Вашего движения к университету будет разным, в зависимости от того, где Вы находитесь: дома или у соседа.
Существует в основном четыре угла ориентирования: истинный и магнитный азимуты, дирекционный угол, румб.
Истинным азимутом называется угол, отсчитанный от северного направления географического (истинного) меридиана по ходу часовой стрелки до заданного направления.
Магнитным азимутом называется угол, отсчитанный от северного направления магнитного меридиана по ходу часовой стрелки до заданного направления.
Дирекционным углом называется угол, отсчитанный от среднего меридиана зоны (оси х-ов) или линии параллельной ему по ходу часовой стрелки. (рис.2).
Истинный азимут на северном полушарии определяется относительно полярной звезды, которая всегда находится над северным географическим полюсом. Магнитный азимут может измерять каждый из нас, имея компас (буссоль), т.к. магнитная стрелка северным концом показывает северный магнитный полюс земли. Дирекционный угол непосредственно на Земле не измеряется, а вычисляется через истинный и магнитный азимуты.
Дирекционный угол, это искаженный угол за счет перехода от кривизны Земли (сфероида) к плоскости. Но этот угол служит для вычисления прямоугольных координат.
Румбом называется угол, отсчитанный от северного или южного направления какого-либо меридиана до заданного направления. Если направление лежит ближе к югу, то румб определяется относительно юга. (рис.2)
Рис.2. a- дирекционный угол, ч-румб
2.Тема: Методы определения координат и топографические съемки.
Теодолитные ходы.
Есть разные методы определения координат точек местности. Есть высокоточные методы, называемые триангуляция, полигонометрия, которые применяются для составления точных карт. Есть менее точный метод, называемый теодолитные ходы, который применяется для составления плана (горизонтальные проекции) малого участка земли. План составляется для проектирования различных объектов, может быть составлен кем угодно, но для этого надо владеть элементарными знаниями по прокладке и вычислению теодолитных ходов, по пользованию геодезическим прибором - теодолит и по методике производства съемки участка местности.
Берется участок местности, на котором необходимо спроектировать и построить небольшие объекты. Необходимо для проектирования иметь план участка в каком-либо масштабе. Для создания плана надо выполнить съемку участка. Для этого создается сеть так называемых опорных точек. Опорная точка, это точка местности, отмеченная на земле чем-либо, например, металлическим штырем или деревянным колышем. Местоположение опорной точки должно быть известно не только на местности, но на плане. Для этого определяют их координаты. Одним из методов определения прямоугольных координат являются теодолитные ходы. Теодолитные ходы состоят из опорных точек, взаимосвязанных друг с другом, расстояние между которыми разрешается от 60 м до 250 м. Теодолитные ходы могут иметь форму замкнутого многоугольника, если участок имеет примерно округлую форму. Теодолитные ходы будут иметь форму вытянутой ломаной линии, если участок работ - вытянутый.
Необходимым условием определения координат точно как при решении прямой геодезической задачи, является наличие исходной опорной точки с заранее известными координатами. Такими исходными точками могут быть опорные точки, у которых координаты определены другими более точными методами, как триангуляция и полигонометрия.
Порядок работ при прокладке теодолитных ходов следующий:
1. Обход участка будущих работ;
2. Измерение горизонтальных углов теодолитом;
3. Измерение длин между точками теодолитного хода рулеткой или мерной лентой;
4. Проверка правильности угловых измерений путем вычисления невязки (неувязки);
5. Вычисление дирекционных углов;
6. Вычисление приращений координат и их невязок;
7. Вычисление координат и построение плана по координатам в заданном масштабе.
Основное вычисление выполняется по формуле прямой геодезической задачи (см.) Остальные измерения и вычисления диктуются необходимостью определения параметров этой задачи.
Основная формула для определения дирекционного угла последующей линии получается по чертежу. При этом начальный дирекционный угол должен быть известным. (Рис. 4) a6 = a1 + 180° - b
|
|
 | |||
 | |||
ю
Ю
Рис. 4
Топографическая съемка.
Слово «топо» в переводе с латинского означает поверхность. В данном случае поверхность земли. «Граф» - означает чертеж. Наиболее доступным чертежом местности является его план, составленный в каком-либо масштабе. Масштаб - это отношение отрезка на плане, равного одному сантиметру к величине этого отрезка на местности в сантиметрах. Например: один сантиметр на плане или на карте равен 500 сантиметрам местности, следовательно, пишем масштаб (его принято писать в виде дроби) 1:500. Если 1 см. На плане равен 10 метрам на местности, то пишем 1:1000, что можно расшифровать так: 1 см. на плане равен 1000 см. на местности.
Для составления плана местности необходимо выполнить топографическую съемку местности. Съемка геодезическими приборами существенно отличается от фотосъемки. Съемки выполняются через геодезические измерения относительно опорных точек. При этом снимаемый объект разлагается на характерные точки. Например, если снимается здание, то характерными точками будут углы здания. Определив положение углов зданий относительно опорных точек каким-либо способом, можем построить план здания, соединив линиями его угловые точки.
Существуют следующие виды топографических съемок:
1. Тахеометрическая
2. Мензульная
3. Аэрофотогеодезическая
Мы остановимся на тахеометрической съемке. Слово «тахео» в переводе с греческого означает - быстро. Следовательно, в буквальном переводе получается быстроизмерительная съемка. Измерения на местности выполняются быстро, например, в летнее время. А план можно чертить не спеша зимой. Во время съемки рисуется абрис снимаемой местности, на котором показывается какая точка где находится и что обозначает: угол здания, угол леса, перекресток дорог, столб и т.д. Абрис не имеет масштаба.
При тахеометрической съемке попутно определяются высоты (отметки) точек местности от уровня моря. Для этого необходимы дополнительные геодезические работы. Высотные работы в геодезии называются нивелированием. Существуют три вида тахеометрической съемки: 1. Полярный метод. 2. Метод перпендикуляров (метод ординат). 3. Метод угловых и линейных засечек. При полярном методе съемки, положение снимаемой точки определяются через угол и длину линии, т.е. определяются полярные координаты. Причем центром полярных координат является опорная точка, над которой стоит теодолит. Ее называют обычно станцией. Осью полярных координат является линия между опорными точками. (Рис.5)
Рис.5. Схема съемок полярным методом и методом ординат.
При любой топографической съемке одновременно с объектами снимается и рельеф (неровности) местности. Для этого определяется высота от уровня моря (отметка) каждой снимаемой точки. Отметки опорных точек определяются заранее.
Относительно опорных точек (станций) находят превышение - разность высот станции и снимаемой точки. Превышение определяется тригонометрическим нивелированием, формула которого получается из чертежа. (рис.6)
Рис.6. Схема тригонометрического нивелирования.
HCT - высотная отметка станции, заранее известна;
HN – высотная отметка снимаемой точки, где стоит рейка;
h – “превышение” (если искомая точка ниже, чем станция, то оно будет отрицательным).
i – высота прибора;
L – высота наведения;
V – угол наклона (измеряется вертикальным кругом теодолита);
I
Д - наклонное расстояние между точками;
d – горизонтальное проложение – проекция измеренной длины на горизонтальную плоскость. Итак отметка равна:
HN = HCT + h,
h – определяется через другие измеренные параметры. Из чертежа видно, что
h = h¢ + i – L,
где i и L – измерены, а получается по формуле тригонометрии:
h¢ = d * tgv, где
d = D¢ * Cosv
Если L = i, т.е. на рейке сделана метка для наведения на уровне высоты прибора, то h = h¢ = dtgv
А угол наклона измеряется вертикальным кругом теодолита при круге право (К.П.) и при круге лево (К.Л.) или только при К.Л.
После окончания всех вычислений, вычерчивается план, на котором строятся и объекты и рельеф. Рельеф показывается горизонталями.
В данном случае горизонталью называется линия, проходящая через точки с одинаковыми высотами (отметками) от уровня моря. Одна линия горизонтали показывает, где проходит на земле одинаковый уровень на какой-либо одной высоте от уровня моря, например, на высоте 130 м. Форма горизонтали повторяет форму рельефа на данном уровне. Для вычерчивания одной горизонтали необходимо искать точки с одинаковой высотой, например, 130 м. И плавно соединить их одной линией. Высоты горизонтальной кратны высоте сечения горизонталей. Высота сечения показывает через какой отрезок по вертикали мы решили мысленно рассекать землю горизонталями.
Заложением называется расстояние между смежными горизонталями. Его величина зависит от величины уклона местности. Чем больше уклон, тем меньше заложение. Уклон зависит от наклона участка земли на данном направлении. В строительной практике принято определять уклон какого-либо направления местности без измерения угла наклона. Обычно за уклон принимают отношение разности высот двух точек земли к величине горизонтального положения между ними. (рис.7.)
рис.7. Схема для определения уклона местности
Таким образом, уклон: 
Знак уклона зависит от знака превышения (разности высот).
На листе карты или плана обычно вычерчивают график заложений, где по вертикали откладывают отрезки между смежными горизонталями (величине заложений), а по горизонтали пишут соответствующие им уклоны или углы наклона на земле. Пользуясь этим графиком, можно найти средний уклон местности между какими-либо точками.
Если хорошо усвоите все выше сказанное, Вы легко выполните контрольную работу №1. Если будет что-либо непонятно по выполнению контрольной работы, просим еще раз прочитать и представить себе как происходят все действия на местности.
Контрольная работа №1.
Задание 1. Вычисление исходных дирекционных углов линий;
Рис.8. К вычислению дирекционных углов сторон теодолитного хода
Дирекционные углы вычисляют по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус горизонтальный угол, справа по ходу лежащий. Следовательно,
; 
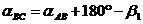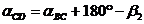
Пример. Вычисление дирекционных углов выполняем столбиком:
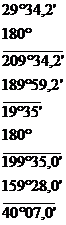
аАВ……………
+
-
аBC……………
+
-
аCD……………
Примечание. Если при вычислении уменьшаемое окажется меньше вычитаемого, то к уменьшаемому прибавляют 360°. Если дирекционный угол получается больше 360°, то из него вычитают 360°.
Задача 2*.Найти координаты хC и уC точки С (рис.8), если известны координаты хВ и уВ точки В, длина (горизонтальное проложение) dВС линии ВС и дирекционный угол аВС этой линии. Координаты точки В и длина dВС берутся одинаковыми для всех вариантов: хВ = -14,02м., уВ = +627,98 м., dВС = 239,14м. Дирекционный угол аВС линии ВС следует взять из решения предыдущей задачи.
Координаты точки С вычисляются по формулам:
; 
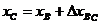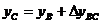
где 
DхВС и DуВС, - приращения координат, вычисляемые из соотношений DхВС = dВС cos a ВС; DуВС = dВС sin a ВС;
Вычисления приращений координат рекомендуется вести на микрокалькуляторе либо по специальным таблицам (например, В.В.Баканова, П.И.Фокин, Таблицы приращений координат/ Под ред. В.Д.Большакова. М., 1976, 1982).
В первом случае знаки приращений координат устанавливаются в зависимости от знаков cos a и sin a. При работе с таблицами для удобства вычислений дирекционный угол следует предварительно перевести в румб, пользуясь табл.1. Тогда
DхВС = ± dВС cos rВС и DуВС = ±dВС sin rВС;
знаки вычисленных приращений координат определяют по названию румба, руководствуясь также табл.1.
При вычислении приращений координат значение дирекционного угла (или румба) округляют до целых минут.
Таблица1. Перевод дирекционных углов в румбы.
Знаки приращений координат
| Четверть | Формула перевода | Знаки приращений координат | ||
| Номер | Название | Dх | Dу | |
| I II III IV | CB ЮВ ЮЗ СЗ | rI = a rII = 180° - a rIII = a – 180° rIV = 360° - a | + - - + | + + - - |
Пример.Дано: dВС = 239,14м.; aВС = 19°35¢. Выполнив вычисления, получаем
DхВС = +225,31м.; DуВС = +80,15м.
Эти вычисления приведены в табл. 7, где в качестве примера дан алгоритм вычислений приращений координат на электронном микрокалькуляторе «Электроника МК-51» с пояснением смысла операций. Вычисления выполнены с контролем полученных результатов по формуле
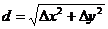
Координаты точки С получаем алгебраическим сложением координат точки В с приращениями по линии ВС, действуя по схеме:
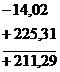
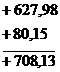
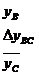
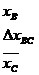
Задачи решают в специальной тетради; решение каждой из них должно сопровождаться схематическим чертежом, соответствующим выполняемому варианту.
В задаче 1 пример подобран так, что вычисленный дирекционный угол aСD последней линии должен получиться на 10°32,8¢ больше, чем исходный дирекционный угол aАВ. Это должно служить контролем правильности решения первой задачи.
Решение задачи 2 непосредственно не контролируется. К ее решению надо подойти особенно внимательно, так как вычисленные координаты хС и уС точки С будут использованы в следующем задании.
Задание 2. Составление топографического плана
Строительной площадки
СОДЕРЖАНИЕ РАБОТЫ
По данным полевых измерений составить и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1м.
Работа состоит из следующих этапов: обработка тахеометрического журнала; построение топографического плана.
ИСХОДНЫЕ ДАННЫЕ
1. Для съемки участка на местности между двумя пунктами полигонометрии П38 и П319 был проложен теодолитно-высотный ход. В нем измерены длины всех сторон (рис.9), а на каждой вершине хода – правый по ходу горизонтальный угол и углы наклона
на предыдущую и последующую вершины.
Рис . 9 Схема теодолитно-высотного хода съемочного обоснования
Результаты измерений горизонтальных углов и линий (табл.2), а также тригонометрического нивелирования (табл.4 и 4а) являются общими для всех вариантов.
Таблица 2. Результаты измерений углов и длин сторон хода
| Номера вершин хода | Измеренные углы (правые) | Длины сторон (горизонтальные проложения), м | |
| ° | ¢ | ||
| ПЗ 8 | 59,2 | ||
| 263,02 | |||
| I | 58.5 | ||
| 239,21 | |||
| II | 20.0 | ||
| 269,80 | |||
| III | 02.8 | ||
| 192,98 | |||
| ПЗ 19 | 08,2 |
Измерение углов производилось оптическим теодолитом 2ТЗ0 с точностью отсчетов по шкаловому микроскопу 0,5¢.
2. Известны координаты полигонометрических знаков ПЗ 8 и ПЗ 19 (т.е. начальной и конечной точек хода):
хПЗ 8 = -14,02
уПЗ 8 = +627,98
хПЗ 19 принимается равным значению хС, а уПЗ 19 – значению уС, полученным при решении задачи 2 в задании 2.
Известны также исходный a0 и конечный an дирекционные углы:
a0 – дирекционный угол направления ПЗ 7 – ПЗ 8; берется в соответствии с шифром и фамилией студента – так же, как и в задании 2; таким образом, a0 = aАВ;
an – дирекционный угол ПЗ 19 – ПЗ 20; для всех студентов принимается равным дирекционному углу aCD линии CD, вычисленному в задаче 1.
Так, в нашем примере a0 = aАВ = 29°34,2¢, an = aCD = 40°07,0¢.
3. Отметки пунктов ПЗ 8 и ПЗ 19 должны быть известны из геометрического нивелирования. При выполнении же задания значение отметки ПЗ 8 следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) ставятся те же цифры, что и в целой части.
Пример.
Зуев ПГС – 85 229 129,129
Иванова СХС – 85 020 120,120
Соколов-Осадчий ГС – 85 002 102,102
Руднев ВК – 85 100 100,100
Отметка ПЗ 19 для всех студентов принимается на 3,282 м. больше отметки ПЗ 8.
4. При съемке участка были составлены абрисы (рис.10,a,б и 4, а-г).
Рис. 10 Абрисы съемки зданий
УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
Рис . 11.
Вычисление дирекционных углов и румбов сторон хода.По исходному дирекционному углу а0 и исправленным значениям углов b хода по формуле для правых углов вычисляют дирекционные углы всех остальных сторон: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус правый (исправленный) угол хода, образованный этими сторонами.
Пример.
аПЗ 8-1 = a0 + 180° - bПЗ 8 = 29°34,2¢ + 180° + 360° - 330°58,9¢ = 238°35,3¢.
Для контроля вычисления дирекционных углов следует найти конечный дирекционный угол аn по дирекционному углу аIII-ПЗ 19 последней стороны и исправленному углу bПЗ 19 при вершине ПЗ 19 (см. рис. 8):
аn = аIII-ПЗ 19 + 180° - bПЗ 19.
Это вычисленное значение аn должно совпасть с заданным дирекционным углом аn. При переходе от дирекционных углов а к румбам r см. табл.1.
Значения дирекционных углов записывают в графу 4 ведомости с точностью до десятых долей минут, а румбов – в графу 5; при этом значения румбов округляют до целых минут.
Вычисление приращений координат. Приращения координат вычисляют по формулам:
Dх = d cos a = ±d cos r; Dу = d sin a = ±d sin r
также, как в задаче 2 задания 2, на микрокалькуляторе или по «Таблицам приращений координат», правила пользования которыми содержатся в предисловии к ним.
Вычисленные значения приращений Dх и Dу выписывают в графы 7 и 8 ведомости с точностью до десятых долей метра. Знаки приращений устанавливают в зависимости от знаков cos a и sin a либо по названию румба, руководствуясь табл.1 [см. также [2, c.215]). В каждой из граф складывают все вычисленные значения Dх и Dу, находя практические суммы приращений координат SDхпр и SDупр.
Нахождение абсолютной и относительной линейных невязок хода; увязка приращений координат.Сначала вычисляют невязки fх и fу в приращениях координат по осям х и у:
fх = SDхпр - SDхт,
fу = SDупр - SDут,
где SDхт = хКОН – хНАЧ
SDут = уКОН - уНАЧ
Примечание. Координаты начальной и конечной точек хода предварительно записывают в графах 11 и 12 ведомости и подчеркивают.
Абсолютную линейную невязку DP хода вычисляют по формуле
и записывают с точностью до сотых долей метра.
Относительная линейная невязка DP/P хода (P – сумма длин сторон хода) выражается простой дробью с единицей в числителе. Если относительная невязка окажется меньше допустимой 1/2000, то невязка fх и fу распределяют, вводя поправки в вычисленные значения приращений координат. Поправки в приращения распределяют прямо пропорционально длинам сторон хода, записанным в графе 6, и вводят со знаком, обратным знаку соответствующей невязки. Значения поправок округляют до сотых долей метра и записывают в ведомости над соответствующими приращениями, следя за тем, чтобы суммы поправок в Dх и Dу равнялись невязке соответственно fх или fу с противоположным знаком. Исправленные приращения записывают в графы 9 и 10; суммы исправленных приращений координат должны быть равны соответственно SDхт и SDут.
Примечание. Примеры в задании подобраны так, чтобы невязка DP/P получалась допустимой. Если эта величина окажется больше 1/2000, значит в вычислениях допущена ошибка. Чаще всего встречаются ошибки: при вычислении дирекционных углов; при переводе дирекционных углов в румбы; в знаках приращений Dх и Dу; при вычислении приращений координат.
Вычисление координат вершин хода.Координаты вершин хода получают путем последовательного алгебраического сложения координат предыдущих вершин хода с соответствующими исправленными приращениями:
хI = хПЗ 8 + Dхпз 8-I; хII = хI + DхI-II и т.д.
Контролем правильности вычислений являются полученные по формулам
хПЗ 19 = хIII + DхIII-ПЗ 19; уПЗ 19 = уIII + DуIII- ПЗ 19
известные координаты конечной точки ПЗ 19 хода.
Обработка тахеометрического журнала.
Литература: [1, §61, 80; 2, §21, 44, 62].
В табл.4 приведена часть журнала тахеометрической съемки, в котором студент должен обработать результаты измерений, выполненных на станции ПЗ 19.
Вычисление места нуля вертикального круга и углов наклона.Из отсчетов по вертикальному кругу при «круге лево» (КЛ) и «круге право» (КП) на предыдущую и последующую станции дважды вычисляют место нуля (МО). Для оптического теодолита 2Т 30, которым была выполнена тахеометрическая съемка.
МО= (КЛ+КП)/2.
При наведении со станции ПЗ 19 на станцию III
Углы наклона v на предыдущую и последующую точки теодолитно-высотного хода вычисляют с контролем по формуле
v = (КЛ-КП)/2 = КЛ-МО = МО-КП
и записывают со своим знаком (плюс или минус) в графу 6. При наблюдении со станции ПЗ 19 на станцию III угол наклона
v = -1°34' - 0°00,75'= -1°34,75' » - l°34,8',
v = +0°00,75' - l°35,5' = -1°34,75’ » -1°34,8'.
Значение МО для направления на ПЗ 20 следует вычислить самостоятельно. Полученные на станции ПЗ 19 два значения МО не должны различаться более чем на двойную точность отсчетного приспособления теодолита; записывают их в графе 5 табл. 4 на соответствующих строчках. Далее из этих двух значений МО выводят среднее арифметическое, округляют его до целых минут и используют для вычисления углов наклона на реечные точки:
v = КЛ - МО.
Углы наклона на реечные точки также записывают в графе 6 табл. 4.
Вычисление горизонтальных проложений и превышений. Значения горизонтальных расстояний между вершинами теодолитно-высотного хода переписывают в графу 7 табл. 4 из ведомости вычисления координат (табл. 3). Вычисление горизонтальных проложений d от станций до реечных точек производят по значениям расстояний D' (табл. 4, графа 2) , полученных по нитяному дальномеру:
d=D' cos2 v.
Превышения h точек относительно станции вычисляют по формуле
h =h' + i - l,
где i — высота инструмента на данной станции; l — высота наводки (табл. 4, графа 9).
При вычислении превышений по сторонам теодолитно-высотного хода, длины которых измерены стальной землемерной лентой,
h' = d tg v.
При определении же превышений на реечные точки, расстояния до которых измерялись по нитяному дальномеру,
Для вычисления d и h' используют микрокалькулятор или тахеометрические таблицы различных авторов. Значения горизонтальных проложений d записывают в графу 7 журнала с округлением до десятых долей метра. Если угол наклона меньше 2°, то горизонтальное проложение принимают практически равным измеренному расстоянию.
Вычисленные значения h' записывают в графу 8 с округлением до сотых долей метра. В графу 10 записывают значения превышений h. Если при визировании на точку труба наводилась на высоту, равную высоте инструмента (l = i), то h = h' и значение превышения из графы 8 без изменения переписывают в графу 10,
Результаты измерений, выполненных на станциях ПЗ 8, I, II и III, обработаны почти полностью, и для этих станций, вместо журнала тахеометрической съемки, в табл. 4а приведена выписка из его граф 1, 3, 7, 10, 11 и 12. Данные в графах 1-4 этой таблицы - общие для всех студентов, а отметки станций и реечных точек в графах 5, 6 каждый студент находит самостоятельно.
Таблица 4а. Выписка из тахеометрического журнала
| Номера Точек наблю- дения | Отсчеты по горизон- тальному кругу | Горизонтальные Проложения | Превы- шения | Отметки | Примечания | |||
| стан-ций | рееч- ных точек | |||||||
| ° | ‘ | |||||||
| Станция П3 8 129,13 | ||||||||
| I | — | -4,17 | ||||||
| 111,2 | -2,32 | 126,81 | ||||||
| 61,8 | +0,20 | 129,33 | ||||||
| 66,0 | - | - | т. 3 - на грунтовой до- роге | |||||
| За | 13,6 | - | - | |||||
| 82,1 | +0,05 | 129,18 | ||||||
| Станция 1 124,95 | ||||||||
| II | — | — | — | -0,30 | ||||
| П38 | — | +4,13 | ||||||
| 149,6 | +4,05 | 129,00 | ||||||
| 68,0 | +2,02 | 126,97 | ||||||
| 11,8 | -0,80 | 124,15 | т. 7,8 - на линии уреза воды | |||||
| 25,2 | - | - | ||||||
| 147,8 | +2,06 | 127,01 | ||||||
| Станция II | 124,65 | |||||||
| III | - | - | - | +0,90 | ||||
| I | - | +0,26 | ||||||
| 98,3 | -0,23 | 124,42 | Т.10-13- | |||||
| на линии уре- за воды | ||||||||
| 24,6 | — | — | ||||||
| 34,4 | — | — | ||||||
| 62,1 | -0,03 | 124,62 | ||||||
| Станция III | 125,53 | |||||||
| П319 | — | — | — | +6,87 | ||||
| II | -0,92 | |||||||
| 102,8 | -0,76 | 124,77 | т. 14-17 - | |||||
| на линии уре- | ||||||||
| 44,1 | -0,63 | 124,90 | за воды | |||||
| 38,0 | — | — | ||||||
| 25,6 | -0,60 | 124,93 |
Вычисление отметок станций. Вычисление отметок станций выполняют в "Ведомости увязки превышений теодолитно-высотного хода и вычисления отметок станций" (табл. 5). Известные отметки НПЗ 8 и НПЗ 19 (с. 32, п. 3 исходных данных), округленные до сотых долей метра, записывают в графу 8 на первой и последней строчках ведомости. Из журна