Цифровые устройства автоматики
Логические функции и логические элементы
Логические переменные и основные операции
Над ними
В отличие от аналоговых устройств, в которых информационный
сигнал может принимать любые значения в некотором диапазоне, в
цифровых устройствах носителем информации является цифровой
двоичный код. Этот код состоит из множества двоичных разрядов,
каждый из которых принимает только два фиксированных значения —
«О» или «1». Двум двоичным цифрам соответствуют два состояния
электронной схемы. Обычно это два фиксированных уровня напря-
жения, которые может принимать сигнал на выходе схемы. Поэтому
все разнообразие математических операций, выполняемых цифро-
выми устройствами, основывается на двоичной системе счисления.
Как уже отмечалось, основанием этой системы служит число два, а
коэффициентами могут быть только две цифры — ноль (0) и едини-
ца (1), которые называют битами (двоичными цифрами).
В любой системе кодирования должно выполняться неравенство
N< Sn, где N — количество кодируемых объектов; S — основание
кода (основание системы счисления); п — длина кода (количество
разрядов в кодовом слове). Например, для записи числа 14 в двоичной
системе счисления необходим четырехразрядный код: 24 = 16, 14 < 16.
Для хранения и обработки информации в виде текстов, формул и
чисел необходимо с помощью бит закодировать около 150 различных
символов (заглавные и строчные буквы латинского и русского алфа-
витов, знаки препинания, математические знаки, десять цифр и т.п.),
т.е. N~ 150. Для этого необходимы 8-разрядные коды (28 = 256). Вось-
миразрядный код называют байтом. Емкость памяти ЭВМ оценива-
ют в килобайтах (кбайт), мегабайтах (Мбайт) и гигабайтах (Гбайт).
Все цифровые устройства основаны на принципе многократного
повторения относительно простых базовых логических схем. Связи
между этими схемами строятся на основе чисто формальных методов.
Инструментом такого построения служит булева алгебра, названная
по имени одного из ее разработчиков — английского математика
Дж. Буля. Применительно к цифровой технике она называется также
алгеброй логики. Логическая переменная имеет только два значения,
которые обычно называются логическим нулем и логической единицей
и обозначаются «0» и «1» или просто 0 и 1. Существует три основные
операции между логическими переменными: конъюнкция (логическое И),
дизъюнкция (логическое ИЛИ) и инверсия (логическое НЕ). Конъ-
юнкция называется также логическим умножением (12.1), дизъюнк-
ция — логическим сложением (12.2), а инверсия — отрицанием (12.3):
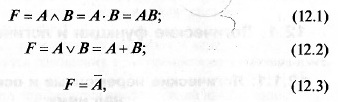
где F — логическая (булева) функция; А и В — логические перемен-
ные.
Значения этих логических функций для всех возможных значений
двух переменных называются таблицей истинности. Для конъюнк-
ции — логического И — функция /"только тогда равна 1, когда оба
ее аргумента А и В равны 1. При дизъюнкции (логическом ИЛИ) F
равна 1 тогда, когда хотя бы один из аргументов (А или В) равен 1.
Отсюда и следуют названия этих функций. Обе эти функции можно
распространить на любое число переменных. Инверсия — логическая
функция только одной переменной.
Операции над логическими переменными выполняются по опре-
деленным правилам. Прежде всего необходимо учитывать принцип
двойственности (теорема де Моргана), который в общем виде запи-
сывается так:
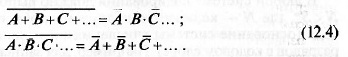
Для преобразования формул алгебры логики с целью их миними-
зации, как и в обычной алгебре, используются скобки, а если их нет,
то сначала выполняется отрицание (инверсия) над отдельными пере-
менными, затем логическое умножение (конъюнкция) и наконец
логическое сложение (дизъюнкция). Если черта (знак инверсии)
стоит над совокупностью букв и знаков, то она выполняется в по-
следнюю очередь. Используются также теоремы алгебры логики.
