Кафедра высшей математики и информационных технологий
Балаш О.С, Высочанская Е.Ю., Носова Е.Г., Попова А.А.
Теория вероятностей
и математическая статистика
Учебное пособие
САРАТОВ
УДК
ББК
Рецензент:
Одобрено:
Учебно-методическим советом Саратовского института (филиала) Российского государственного торгово-экономического университета
Балаш О.С, Высочанская Е.Ю., Носова Е.Г., Попова А.А.
Теория вероятностей и математическая статистика. Учебное пособие / Балаш О.С, Высочанская Е.Ю., Носова Е.Г., Попова А.А. – Саратов: Саратовский ин-т (филиал) РГТЭУ, 2011. с.
ISBN 5-
Пособие содержит
УДК
ББК
| ISBN 5- | ã Балаш О.С, Высочанская Е.Ю., Носова Е.Г., А.А. Попова, 2011 |
 |
СодерЖание
Введение.......................................................................................................... 4
1. Основные понятия теории вероятностей........................................... 5
1.1. Классификация событий................................................................. 5
1.2. Классическое определение вероятности события................. 10
1.3. Статистическое определение вероятности события............. 12
1.4. Геометрическое определение вероятности события.............. 13
1.5. Элементы комбинаторики............................................................. 15
1.6. Теоремы сложения и умножения вероятностей...................... 23
1.7. Формула полной вероятности. Формула Байеса................... 28
2. Повторные независимые испытания................................................ 35
2.1. Формула Бернулли........................................................................... 35
2.2. Приближенные формулы Пуассона и Лапласа........................ 40
Варианты контрольных заданий........................................................... 47
Введение
Предлагаемые методические указания ставят своей целью помочь студентам освоить теоретический и практический материал.
Данные указания содержат программу, вопросы для теоретического опроса, упражнения для самостоятельной работы и контрольные задания по курсу «Теория вероятностей и математическая статистика», а также приводится список литературы, в которой можно найти материал по всем вопросам указанного курса.
Каждая тема включает краткий теоретический материал, решения некоторых типовых задач и необходимые статистические таблицы. Пособие содержит большое количество примеров для самостоятельной работы с ответами. Для закрепления материала студентам предлагается выполнить контрольные задачи по рассматриваемым темам.
Основные понятия теории вероятностей
Классификация событий
Теория вероятностей — это раздел математики, изучающий закономерности случайных явлений.
Основным объектом изучения теории вероятности является так называемое случайное событие.
Под испытанием (опытом, экспериментом) понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания может произойти или не произойти, поэтому событие — это возможный исход, результат испытания.
Например, выигрыш автомобиля по билету денежно-вещевой лотереи или выход бракованного изделия с конвейера предприятия.
События обозначаются прописными (заглавными) буквами латинского алфавита: А, В, С.
Событие называется достоверным, если в результате испытания оно не может не произойти в условиях данного опыта или явления.
Событие называется невозможным, если в результате испытания оно не может произойти при выполнении определенного комплекса условий.
Например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
События называются равновозможными,если в результате испытания по условиям симметрии ни одно из этих событий не является объективно более возможным, т.е. нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Например, бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти одно из них.
Например: события, состоящие в том, что в семье из двух детей: А — «два мальчика», В — «один мальчик, одна девочка», С — «две девочки» — являются единственно возможными.
Элементарными событиями (простейшими исходами) называются такие исходы испытания, которые являются неделимыми, равновозможными и служат составными элементами других более сложных случайных событий.
Все элементарные события, в сумме составляющие достоверное, образуют пространство элементарных событий Ω(ω). С математической точки зрения пространство элементарных событий Ω – это некоторое множество, а элементарные события ωi – его элементы: Ω={ωi, i = 1, ...}. Любое событие А рассматривается как некоторое подмножество множества Ω, то есть АÌ Ω.
Сложное (неэлементарное) событие – это событие, которое может иметь место при нескольких различных элементарных событиях.
Например, будем бросать игральную кость с пронумерованными гранями (1, 2, 3, 4, 5, 6). Предположим, что геометрический центр кубика совпадает с его центром тяжести. Это делает равновозможными выпадение любой его грани. Элементарные события – это выпадение определенной грани. Пространство элементарных исходов Ω состоит из следующих элементарных исходов: ω1={1}, ω2={2}, ω3={3}, ω4={4}, ω5={5}, ω6={6}.
Если при бросании кубика нас будет интересовать случай выпадения четного числа очков, то этому сложному событию соответствует три исхода - 2, 4, 6. Событие А (выпадение четной цифры) можно записать как A={ω2, ω4, ω6}.
Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят, что А влечет за собой событие В (или В включает событие А). В этом случае событие А так же называют частным случаем события В и обозначают АÌ В.
Если одновременно АÌ В и ВÌ А, то в этом случае события А и В называются равносильными.
Два события A и В называются несовместными, если наступление одного из них исключает наступление другого. В противном случае события называются совместными.
Несколько событий образуют полную группу (полную систему), если они являются единственно возможными и несовместными исходами испытания.
Частным случаем событий, образующих полную группу, являются противоположные события. Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Событие, противоположное событию А,обозначается 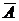 .
.
Суммой (объединением) двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В, то есть С = А + В или 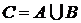 .
.
Произведением (пересечением) двух событий А и В называется событие С, состоящее в совместном появлении и события А, и события В, то есть С = А·В или 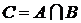 .
.
Операции сложения и умножения событий обладают следующими свойствами:
· А+В = В+А — коммутативность сложения;
· А+(В+С) = (А+В)+С — ассоциативность сложения;
· АВ = ВА — коммутативность умножения;
· А(ВС) = (АВ)С — ассоциативность умножения;
· А(В+С) = АВ+АС; А+ВС= (А+В)(А+С)– законы дистрибутивности.
Пример 1.1.1.Опыт состоит в бросании двух монет. Рассматриваются следующие события:
А — появление герба на первой монете; В — появление цифры на первой монете; С — появление герба на второй монете; D — появление цифры на второй монете; Е — появление хотя бы одного герба; F — появление хоты бы одной цифры; G — появление одного герба и одной цифры; Н — не появление ни одного герба; К — появление двух гербов.
Определить каким событиям этого списка эквивалентны следующие события: а)  С; б)
С; б) 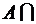 С; в)
С; в) 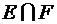 ; г)
; г) 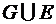 ; д)
; д) 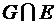 ; е)
; е) 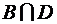 ; ж)
; ж)  .
.
Решение.
а)  С—событие, состоящее в появлении или события А (герб на первой монете), или события С (герб на второй монете), или в совместном появлении событий А и С (гербы на первой и второй монетах), т.е. в появлении хотя бы одного герба, значит
С—событие, состоящее в появлении или события А (герб на первой монете), или события С (герб на второй монете), или в совместном появлении событий А и С (гербы на первой и второй монетах), т.е. в появлении хотя бы одного герба, значит  С=Е;
С=Е;
б)  С — событие, состоящее в совместном появлении событий А и С (гербы на первой и на второй монетах), т.е. появление двух гербов
С — событие, состоящее в совместном появлении событий А и С (гербы на первой и на второй монетах), т.е. появление двух гербов  С = К;
С = К;
в) 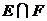 — событие, состоящее в совместном появлении события Е (герб на первой монете или герб на второй монете, или на обеих монетах) и события F (цифра на первой монете, или цифра на второй монете, или цифры на обеих монетах), т. е. появление одного герба и одной цифры:
— событие, состоящее в совместном появлении события Е (герб на первой монете или герб на второй монете, или на обеих монетах) и события F (цифра на первой монете, или цифра на второй монете, или цифры на обеих монетах), т. е. появление одного герба и одной цифры: 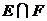 = G;
= G;
г-д) Так как событие Е состоит в появлении герба на первой монете, или на второй, а событие G в появлении одного герба и одной цифры, то G включено в Е, значит  = Е, а
= Е, а 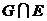 = G;
= G;
е) 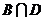 — событие, состоящее в совместном появлении событий В (цифра на первой монете) и D (цифра на второй монете), т. е. в непоявлении ни одного герба:
— событие, состоящее в совместном появлении событий В (цифра на первой монете) и D (цифра на второй монете), т. е. в непоявлении ни одного герба: 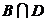 = Н;
= Н;
ж) Событие К — появление двух гербов включено в событие Е, то есть 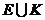 = Е.
= Е.
Задачи
1.1. Указать события случайные, достоверные и невозможные среди перечисленных:
А — при бросании игральной кости выпало простое число очков;
В — появление не более 18 очков при бросании трёх игральных костей;
С — появление более 12 очков при однократном бросании двух игральных костей;
D — появление слова «декан» при случайном наборе букв а, е, д, к, н;
Е — появление в окошечке счётчика трёхзначного числа, составленного из цифр 1, 2, 3 в случайном наборе и кратного 5;
F — наугад выбранное двузначное число не больше 100.
(Ответ: события В, F – достоверные; события С, Е – невозможные; события А, D – случайные.)
1.2. Являются ли несовместными следующие события:
а) Опыт — бросание монеты.
События: А1 — появление герба;
А2 — появление цифры.
б) Опыт — бросание двух монет.
События: В1 — появление герба на 1-й монете;
В2 — появление цифры на 2-й монете.
в) Опыт — два выстрела по мишени.
События: С1 — ни одного попадания;
С2 — одно попадание;
С3 — два попадания.
г) Опыт — два выстрела по мишени.
События: Е1 — хотя бы одно попадание;
Е2 — хотя бы один промах.
д) Опыт — вынимание двух карт из колоды.
События: D1 — появление двух чёрных карт;
D2 — появление туза;
D3 — появление дамы.
(Ответ: а) да; б) нет; в) да; г) нет; д) нет.)
1.3. Назвать противоположные для следующих событий:
А — выпадение двух гербов при бросании двух монет;
В — появление белого шара при вынимании одного шара из урны, в которой 2 белых и 3 чёрных шара;
С — три попадания при трёх выстрелах;
D — хотя бы одно попадание при 5 выстрелах;
Е — не более двух попаданий при 5 выстрелах
F — выигрыш одного игрока при игре в шахматы.
(Ответ: 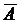 — выпадение хотя бы одной цифры;
— выпадение хотя бы одной цифры; 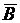 — появление чёрного шара;
— появление чёрного шара; 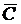 — хотя бы один промах;
— хотя бы один промах; 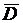 — все 5 промахов;
— все 5 промахов; 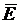 — более двух попаданий;
— более двух попаданий; 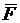 — выигрыш второго или ничья.
— выигрыш второго или ничья.
1.4. Укажите случайные, достоверные и невозможные события среди перечисленных:
А — появление чётного числа очков при однократном бросании игральной кости;
В — наугад выбранное трёхзначное число не больше 1000;
С — получение оценки «неудовлетворительно» на экзамене;
D — появление белого шара при вынимании одного шара из урны, в которой 4 чёрных и 5 красных шаров;
Е — два попадания при трёх выстрелах;
(Ответ: достоверное событие В; невозможное событие D; случайные события А, С, Е).
1.5. Пусть событие А означает выпадение на игральном кубике чётного числа очков, событие В — число очков, кратное 3. Указать смысл событий: а) А  В; б) А
В; б) А  В.
В.
(Ответ: а) А  В — сумма событий: или чётное число очков, или кратное 3 (т.е. 2, 4, 3, 6); б) А
В — сумма событий: или чётное число очков, или кратное 3 (т.е. 2, 4, 3, 6); б) А  В — произведение событий: выпадение на кубике чётного числа очков кратного трём (т.е. 6)).
В — произведение событий: выпадение на кубике чётного числа очков кратного трём (т.е. 6)).
