Аналитической геометрии на плоскости

Вопросы для самопроверки

1. Напишите формулу для вычисления расстояния между двумя точками на плоскости.

2. Напишите уравнение прямой с угловым коэффициентом. В чем состоит геометрический смысл углового коэффициента?

3. Запишите уравнение прямой, проходящей через две точки на плоскости.

4. Как найти угловой коэффициент прямой, если дано ее общее уравнение?

5. Как вычислить угол между прямыми, заданными уравнениями с угловыми коэффициентами ?

6. Как найти координаты точек пересечения двух прямых, если даны их уравнения?

Рекомендации к решению задания

Пусть даны координаты вершин DABC: A(1; 3); B(10; 9); C(15; 1). Требуется найти : 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) тангенс угла В; 4) уравнение высоты CD; 5) уравнение медианы AE; 6) уравнение прямой, проходящей через точку С параллельно стороне AB; 7) сделать чертеж.

1. Расстояние между точками A(x₁; y₁) и B(x₂; y₂) определяется по формуле

,

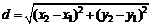поэтому .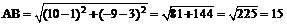

2. Уравнение прямой, проходящей через точки A(x₁, y₁) и B(x₂, y₂), имеет вид

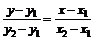. (1)

Подставив в уравнение (1) координаты точек A и B, получим уравнение стороны AB:

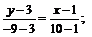
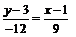; 3y–9= –4x+4; –4x–3y+13=0 (AB).

Решив последнее уравнение относительно y, получим

.

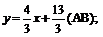
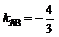Подставив в уравнение (1) координаты точек В и С, получим уравнение прямой ВС:

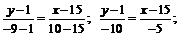y–1=2(x–15); 2x–y–29=0(BC); y=2x–29; k_BC=2.

3. Известно, что тангенс угла j между двумя прямыми вычисляется по формуле

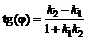. (2)

Искомый угол B образован прямыми AB и BC. Угловые коэффициенты этих прямых соответственно равны 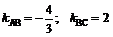, поэтому тангенс угла В будет вычисляться следующим образом:

.

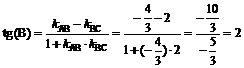4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид

y–y₁=k(x–x₁). (3)

Высота CD перпендикулярна стороне AB. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как 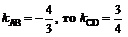. Подставив в уравнение (3) координаты точки C и угловой коэффициент высоты CD, получим:

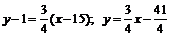(CD).

5. Чтобы найти уравнение медианы AE, определим сначала координаты точки E, которая является серединой стороны BC, применяя формулы деления отрезка пополам:

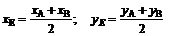, (4)

.

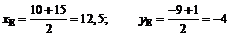Подставив в уравнение (1) координаты точек A и E, находим уравнение медианы:

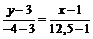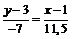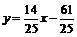; ; (AE).

6. Так как искомая прямая параллельна стороне AB, то ее угловой коэффициент будет равен угловому коэффициенту прямой AB. Подставив в уравнение (3) координаты точки C и угловой коэффициент 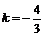, получим 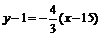, 4x+3y–63=0 (KF).

7. Сделаем чертеж (рис. 1).

Задание 2

Задачи 21–40. Даны координаты вершин DABC. Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) тангенс угла В; 4) уравнение высоты CD; 5) уравнение медианы AE; 6) уравнение прямой, проходящей через точку С параллельно стороне AB; 7) сделать чертеж.

Номер задачи	A	B	C
	(–2; –3)	(0; 7)	(8; 3)
	(5; 4)	(7; 14)	(15; 10)
	(–1; 5)	(1; 15)	(9; 11)
	(0; 3)	(2; 13)	(10; 9)
	(3; 0)	(5; 10)	(13; 6)
	(2; –5)	(4; 5)	(12; 1)
	(–3; –2)	(–1; 8)	(7; 4)
	(4; 1)	(6; 11)	(14; 7)
	(–4; –1)	(–2; 9)	(6; 5)
	(1; 2)	(3; 12)	(11; 8)
	(–8; –3)	(4; –12)	(8; 10)
	(–7; 6)	(2; –6)	(7; 4)
	(–5; 7)	(4; –5)	(9; 5)
	(–3; 5)	(6; –7)	(11; 3)
	(–6; 10)	(3; –2)	(8; 8)
	(–4; 10)	(5; –4)	(10; 6)
	(–8; 9)	(1; –3)	(7; 7)
	(–9; 12)	(0; 0)	(5; 10)
	(–2; 11)	(7; –1)	(12; 9)
	(–1; 4)	(8; –8)	(13; 2)

Тема 3. ВЕКТОРЫ.

УРАВНЕНИЯ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Вопросы для самопроверки

1. Что называется вектором? Запишите его координаты.

2. Какие линейные операции можно выполнять с векторами?

3. Что называется скалярным произведением двух векторов?

4. Дайте определение векторного произведения двух векторов. Запишите формулу вычисления векторного произведения двух векторов, заданных координатами.

5. Напишите уравнение плоскости, проходящей через точку перпендикулярно заданному вектору.

6. Напишите каноническое уравнение прямой в пространстве.

7. Как найти объем пирамиды, построенной на трех некомпланарных векторах?

Рекомендации к решению задания

Пусть даны координаты вершин пирамиды АВСD: А(8; 6; 7); В(–2; 2; –1); С(–3; 4;–3) D(5; 8; 5). Требуется:

1) записать векторы 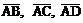в системе орт 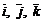и найти модули этих векторов;

2) найти косинус угла между векторами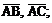

3) найти проекцию вектора 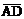на вектор ;

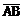4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение грани АВС.

Произвольный вектор представляется в системе орт 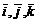формулой

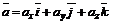, (1)

где а_х, а_у, а_z – координаты вектора .

Если заданы точки М(х₁; у₁; z₁) и N(х₂; у₂; z₂), то координаты вектора 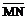соответственно равны а_х= х₂ – х₁; а_у=у₂–у₁; а_z=z₂–z₁ и вектор имеет вид

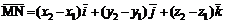. (2)

1. Применим формулу (2) для векторов 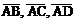, получим векторы: ; ; .

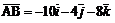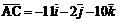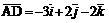Если вектор задан координатами, то модуль этого вектора вычисляется по формуле

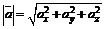. (3)

Применяя выражение (3), получим:

;

;

.

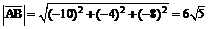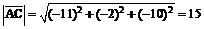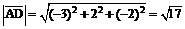2. Из формулы скалярного произведения вектора на вектор 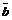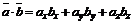имеем:

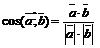. (4)

Применяя формулу (4) для векторов 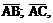получим:

.

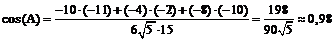Проекция вектора на вектор 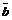есть 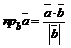, тогда

.

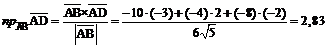4. Площадь грани АВС будем вычислять по формуле 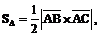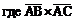– векторное произведение векторов.

Найдем векторное произведение векторов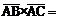

.

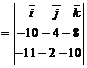
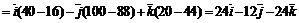Определим модуль векторного произведения:

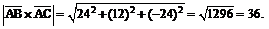
Тогда .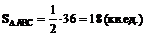

5. Объем пирамиды АВСD определим по формуле

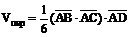. (5)

Найдем смешанное произведение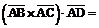

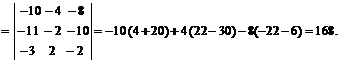
Тогда .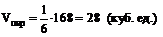

6. Чтобы получить уравнение грани АВС, нужно составить уравнение плоскости, проходящей через точки А, В, С. Это уравнение имеет вид

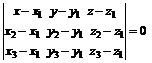. (6)

Тогда ; ;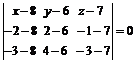

.

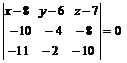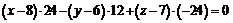Разделим на 12 обе части уравнения, в результате уравнение грани будет иметь вид .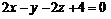

Задание 3

Задачи 41–60. Даны координаты вершин пирамиды АВСD. Требуется:

1) записать векторы 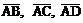в системе орт 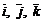и найти модули этих векторов;

2) найти косинус угла между векторами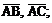

3) найти проекцию вектора 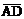на вектор ;

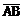4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение грани АВС.

Номер задач	А	В	С	D
	(2; 1; 0)	(3; –1; 2)	(13; 3; 10)	(0; 1; 4)
	(0; –2; –1)	(2; 4; –2)	(3; 2; 0)	(–11; 8; 10)
	(5; –1; –4)	(9; 3; –6)	(7; 10;–14)	(5; 1; –3)
	(1; –4; 0)	(5; 0; –2)	(3; 7; –10)	(1; –2; 1)
	(–3; –6; 2)	(1; –2; 0)	(–1; 5; –8)	(–3; –4; 3)
	(4; 8; 1)	(0; 4; 3)	(2; 15; –7)	(0; 6; 4)
Номер задач	А	В	С	D
	(2; 4; –4)	(0; 11; –12)	(–2; 0; –2)	(–2; 2; –1)
	(3; 3; –3)	(7; 7; –5)	(3; 5; –2)	(5; 14; –13)
	(6; 9; –5)	(8; 2; 3)	(4; –2; 5)	(4; 0; 6)
	(–4; –2; 3)	(6; 2; 11)	(–5; 0; 1)	(3; 4; 9)
	(2; –6; 2)	(12; –2; 10)	(1; –4; 0)	(9; 0; 8)
	(–2; –2; –8)	(0; –4; –6)	(10; 0; 2)	(7; 2; 0)
	(1; 0; –8)	(11; 4; 0)	(0; 2; –10)	(8; 6; –2)
	(4; –1; 0)	(3; 1; –2)	(14; 3; 8)	(11; 5; 6)
	(2; –3; 1)	(6; 1; –1)	(4; 8; –9)	(2; –1; 2)
	(9; 3; –6)	(7; 10; –14)	(5; –1; –4)	(5; 1; –3)
	(–1; –5; 4)	(9; –1; 12)	(–2; –3; 2)	(6; 1; 10)
	(–4; 5; –5)	(7; 7; 5)	(–3; 3; –3)	(4; 9; 3)
	(3; –3; –2)	(13; 1; 6)	(2; –1; –4)	(10; 3; 4)
	(–7; 1; 1)	(–8; 3; –1)	(3; 5; 9)	(0; 7; 7)