Кинетическая кинетическая кинетическая

Энергия модели энергия поступ. энергия вращат.

Движущ.звеньев движущ.звеньев

В нашем случае:

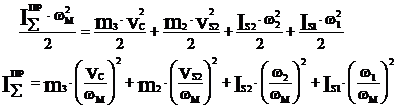
w_м = w₁

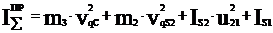
Лекция 4.

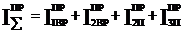
Приведение масс основано на равенстве кинетических энергий реальных звеньев и звена приведения одномассовой модели.

Если требуется определить какую-либо составляющую 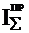, например 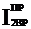, то записывают равенство:

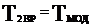
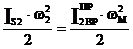
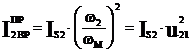
2.4.2 Приведение сил.

А_Σ –работа суммарного приведенного момента на его возможное перемещение.

Т – Т_нач = А_Σ

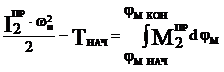
(1)

Приведение сил основано на равенстве секундных работ (мощностей) реальных сил и моментов, приложенных к звеньям механизма, на их возможных перемещениях и суммарного приведенного момента, приложенного к звену приведения, на его возможное перемещение.

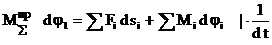
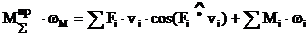
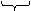
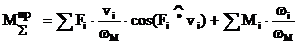
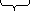
Передат передаточ

Функция отношение

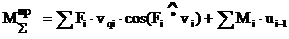
Вместо силы 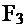– момент .

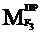Если необходимо определить какую-либо составляющую суммарного приведенного момента, например 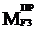, то необходимо записать равенство:

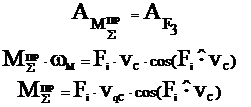
§2.5 Вывод формулы для определения закона движения звена приведения в форме кинетической энергии (определение ω_м).

из выражения (1) получаем, что w_м равна

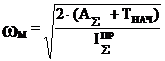
2.5.1 Определение А_Σ(графический метод).

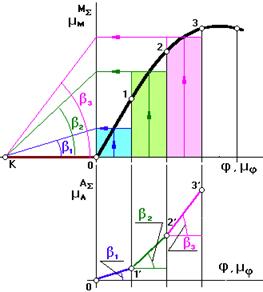
Для определения А_Σ необходимо построить график .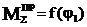

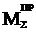определяется по вышеприведенным зависимостям.

График А_Σ строится методом графического интегрирования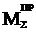

Суть метода: на продолжении оси абсцисс слева выбирается произвольный отрезок интегрирования ОК, чем он длиннее, тем более пологим будет график А_Σ . Затем площадь под кривой М(φ₁) на каждой итерации заменяется площадью равновеликого прямоугольника.

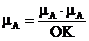
2.5.2 Определение закона движения звена приведения в дифференциальной форме (определение e звена приведения).

Чтобы избавиться от интеграла в (1), продифференцируем (1) по обобщенной координате φ_м, получим

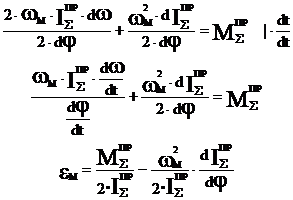
(3)

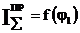2.5.3 Определение 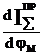графическим методом .

Строим график .

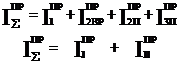
Const var

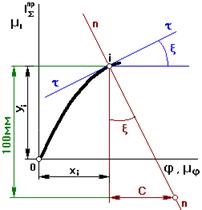
В соответствии с определением производной проведем касательную к кривой в точке i и определим тангенс угла наклона этой касательной. Для этого проведем нормаль через точку i. Тогда

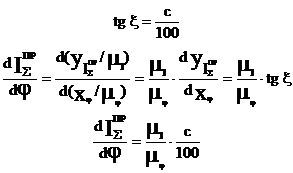
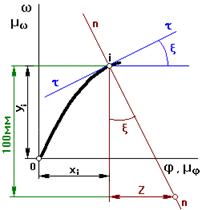
2.5.4 Определение e_модели по известному графику w_м=f(φ₁).

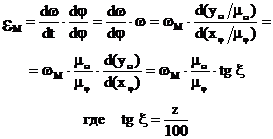
§2.6 Режимы работы машинного агрегата.

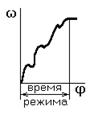
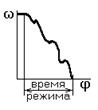
а) разгон б) торможение (выбег)

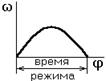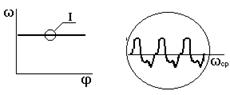в) безударный останов г)

рис. 2.6

а),б),в) – неустановившийся режим;

г) – установившийся режим.

2.6.1 Определение законов движения звена приведения одномассовой динамической модели при неустановившемся режиме работы машинного агрегата.

Угловая скорость определяется по (2).

Угловое ускорение определяется по (3).

Время режима определяется по формуле:

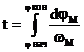
2.6.2 Определение законов движения для установившегося режима работы .

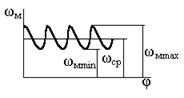
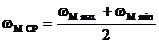
Отклонения угловой скорости от среднего уровня характеризуется коэффициентом неравномерности d

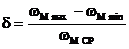
Коэффициент d определяется экспериментально и для различных машин имеет значения:

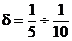машины ударного действия (прессы, молоты)

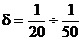полиграфические машины (насосы)

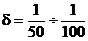электрогенераторы переменного тока

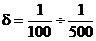электрогенераторы постоянного тока

ЛЕКЦИЯ 5.

Для определения угловой скорости

,

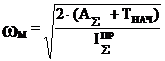где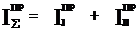

Const var

Для того чтобы удерживать колебания угловой скорости w_м в заданных пределах, определяемых коэффициентом неравномерности d, первая группа звеньев должна иметь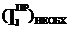

2.6.3 Вывод формулы для определения .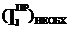

Изменение w_м от w_{м_max} до w_{м_min} приводит к изменению кинетической энергии первой группы звеньев (ΔТ_I), которое равно:

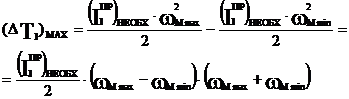
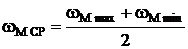
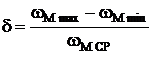
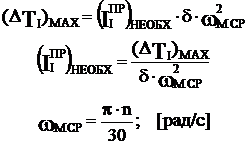(2)

При установившемся режиме работы при определении w_м формулу (1) напрямую использовать нельзя, т.к. неизвестно Т_нач, поэтому задачу решают, используя метод Мерцалова (см. учебник).

§2.7 Определение реакций в кинематических парах рычажных механизмов без учета трения.

Данная задача может быть решена:

1. аналитическим способом;

2. графическим способом (см.ДЗ №2).

Аналитический способ:

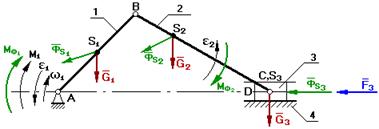Изобразим схему кривошипно-ползунного механизма.

Дано:

F₃, G₁, Ф_S1, M_Ф1, G₂,

Ф_S2, М_Ф2, G₃, Ф_S3,

w_i, e_i, v_i, a_i.

Определить:

М₁ и Q_ij

Задачу начинают решать с того звена, к которому приложена известная сила или момент. Кроме того, введем понятие входной шарнир (проекции реакции Q на оси х и у положительны) и выходной шарнир (проекции реакции Q на оси - отрицательны).

Расстояние от входного шарнира до центра масс звена – р, а расстояние от выходного шарнира до центра масс звена – q.

Звено 1

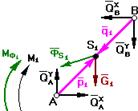
Шарнир А - входной

Шарнир В - выходной

Звено 2

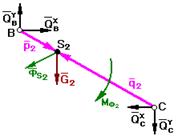
Шарнир В - входной

Шарнир С - выходной

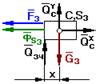Звено 3

При решении задачи используется принцип Даламбера

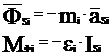
3 звено:

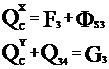
2 звено:

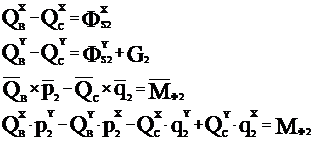
1 звено:

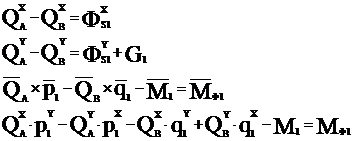
Составим систему уравнений в матричной форме:

неизвестные

QAx

QAy

QBx

QBy

QCx

QCy

Q34

M1

F3+ФS3

=

х

QAx

G3

QAy

ФS2x

-1

QBx

ФS2y+G2

-1

QBy

MФ2

p2y

-p2x

-q2y

q2x

QCx

ФS1x

-1

QCy

ФS2y+G2

-1

Q34

MФ1

p1y

-p1x

-q1y

q1x

-1

M1

B A x

Эта система решается методом Гаусса.

§2.8 Учет трения при определении реакций в кинематических парах.

Трение является сложным физико-химическим процессом, сопровождающийся выделением тепла. Это вызвано тем, что перемещающиеся тела оказывают сопротивление относительному движению. Мерой интенсивности сопротивления относительному перемещению является сила (момент) трения.

Различают трение качения, трение скольжения, а также сухое, граничное и жидкостное трение.

Если суммарная высота микронеровностей взаимодействующих поверхностей:

· больше, чем высота слоя смазки, то - сухое трение.

· равна высоте слоя смазки, то -граничноетрение.

· меньше, чем высота слоя смазки, то - жидкостное .

2.8.1 Учет трения в поступательной кинематической паре.

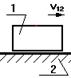Без учета трения реакция направлена по нормали к взаимодействующим поверхностям. При учете трения результирующая реакция Q₂₁ отклоняется от общей нормали на угол трения j в сторону противоположную направлению движения.

без учета трения с учетом трения

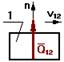
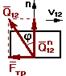F_тр=Qⁿ₁₂^.tg j

tg j= f

F_тр=Qⁿ₁₂^.f

Коэффициент трения f определяется экспериментально и зависит от многих факторов.

2.8.2 Учет трения во вращательной кинематической паре.

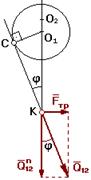
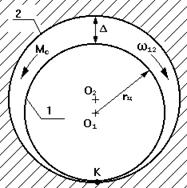
1 - цапфа

r_ц - радиус цапфы

Δ - зазор

r - радус круга трения;

r = О₁С

Из ΔО₁СК à 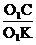= sin j à О₁С = О₁К sin j

M_c= Q₁₂^.О₁С = Q₁₂^. r_ц^.sin j

При малых углах j sin j ≈ tg j = f . Тогда :

M_c= Q₁₂^. r_ц^.f

При учете трения во вращательной КП результирующая реакция отклоняется от общей нормали на угол трения j и проходит касательно к кругу трения радиуса r

ЛЕКЦИЯ 6.

2.8.3 Краткие сведения по определению КПД (h) машинного агрегата.

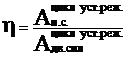КПД машинного агрегата равен отношению работы сил полезного сопротивления к работе движущих сил за цикл установившегося режима.

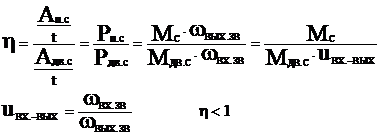
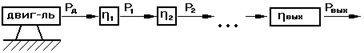а) определение КПД при последовательном соединении механизмов.

P_вход = Р_д

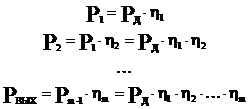
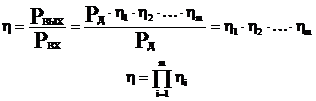
б) определение КПД при параллельном соединении механизмов.

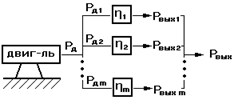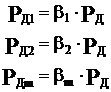
где b_i – коэффициенты распределения мощности.

b₁ + b₂ + b₃ +… + b_m = 1

Каждый b определяется назначением специалиста.

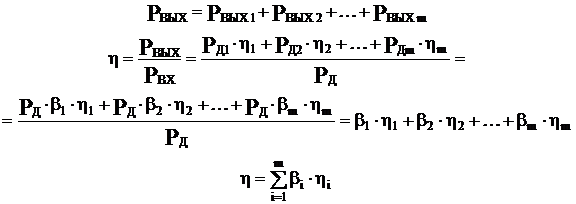
Глава3. Основные сведения о виброзащите машинного агрегата.

Вибрации нашли полезные применения в технике. Примерами этого являются различные вибромассажеры, вибротранспортеры и т.д. Однако работа с инструментом, основанном на вибрации, приводит к профессиональным травмам и заболеваниям. Основные мероприятия, связанные с выявлением источника вибрации, с целью последующего снижения его виброактивности или полного его устранения, называют виброзащитой.

Виброзащита осуществляется по следующим основным направлениям:

1. Уменьшение активности источника с помощью статического уравновешивания механизмов (полного или частичного), а также уравновешивания роторов.

2. Изменение конструкции объекта: установка гасителей колебаний, демпферов, виброизоляторов.

§3.1 Статическое уравновешивание рычажных механизмов.

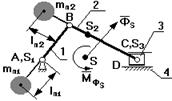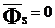Если , то такой механизм называется статически уравновешенным.

Если 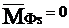, то такой механизм называется моментно-уравновешенным.

Рассмотрим случай, когда необходимо уравновесить статически,

т.е. 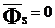. Этого можно добиться только тогда, когда 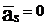, т.к.

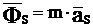S à A

Когда центр масс совмещен с А, то он становиться неподвижным. Этого добиваются с помощью двух противовесов, один из которых устанавливается на продолжении шатуна, а другой на продолжении кривошипа.

Для того чтобы рассчитать массы противовесов, применяют метод замещающих масс, суть которого заключается в том, что масса каждого звена условно разноситься по двум точкам. При этом должны выполняться следующие условия:

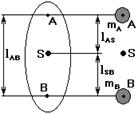разнесем массу этого звена по точкам А и В так, чтобы положение центра масс не изменилось.

m = m_A + m_B

l_AB = l_AS + l_BS

m_A l_AS = m_B l_BS

Сосредоточим массу 3-го звена в т.С

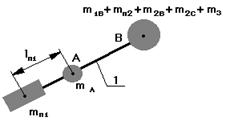
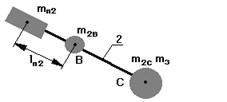Массу 2-го звена разнесем по шарнирам В и С. Если на продолжении звена 2 поставить противовес массой m_пр2 и на расстоянии от т.В равное l_пр2, то центр масс звеньев 2 и 3 переместиться в т.В, при этом

m_пр2^.l_пр2 = (m_2C + m_3C)^.l_BC

При этом либо задаются массой противовеса и определяют l_пр2, либо задаются l_пр2 и определяют массу противовеса.

m_пр1^.l_пр1 = (m_1B + m_пр2+ m_2В+ m_2C+ m_3C)^.l_AB

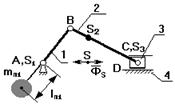После всех указанных мероприятий, центр масс переместиться в точку А, однако невсегда конструктивно возможно установить противовес на продолжении шатуна и ограничиваются установкой противовеса на звене 1. В этом случае центр масс системы смещают на линию АС, и этот центр масс перемещается с постоянным ускорением: а = const

В этом случае механизм – частично статически уравновешанный, его нежелательно устанавливать на высоком фундаменте, т.к. главный вектор сил инерции создает опрокидывающий момент, что недопустимо.

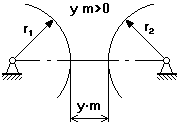
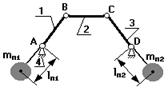В четырехшарнирном механизме центр масс системы разноситься по точкам А и D, а противовесы устанавливаются на продолжении звеньев 1 и 3.

§3.2 Балансировка ротора (лаб. раб. №9).

Ротор – тело любой геометрической формы, имеющее свое основное движение – движение вращения (коленвал, колесо турбины и т.д.).

Пусть в силу каких-либо причин центр масс ротора смещен от оси вращения О на постоянную величину е.

1. w=0 à на опоры действует только сила тяжести G=mg.

2. w=соnst

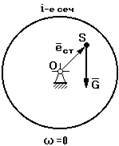
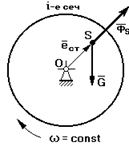1) 2)

Если заменить воздействие опоры реакцией и записать условие статического равновесия (по Даламберу):

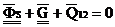
Из рассмотрения данного треугольника следует, что при вращении ротора на его опоре возникает знакопеременная нагрузка Q₁₂, которая достигает максимума, когда Ф_S и G направлены вниз, и минимума, когда эти вектора направлены по вертикали в разные стороны.

Состояние ротора , характеризующегося таким распределением масс, при котором на его опорах возникает знакопеременная нагрузка, называется неуравновешанностью ротора.

Причины вызывающие неуравновешанность ротора:

1. неточность изготовления ротора;

2. неточность сборки;

3. различные включения при отливке частей ротора;

4. перепады температур.

Мерой неуравновешенностью ротора является дисбаланс ( 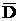) – вектор, направленный по Ф_S и отличающийся от него в w² раз:

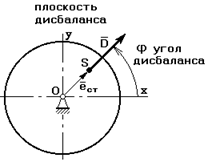
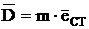,[г^.мм]

Для того чтобы определить величину и направление D, в рассмотрение вводят плоскость дисбаланса, в которой этот вектор расположен, и угол дисбаланса.

Мероприятие, связанное с определением величины и направления D, с целью его последующего уменьшения, называется уравновешиванием ротора.

Существуют 3 вида неуравновешанности:

1. статическая;

2. моментная;

3. динамическая (общий случай).

ЛЕКЦИЯ 7.

3.2.1 Статическая неуравновешанность ротора и способы ее устранения.

Статическая неуравновешанность характеризуется тем, что главная центральная ось инерции ротора расположена параллельно оси его вращения, а центр масс ротора смещен от оси вращения на величину е статическое.

Статическая неуравновешанность проявляется в статике: если ось вращения ротора установить на призмы, то ротор, стремясь занять положение устойчивого положения равновесия, будет поворачиваться.

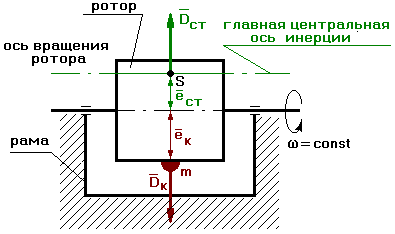
При вращении ротора возникает статический дисбаланс D_cт. Для устранения статической неуравновешанности по линии действия D_cт устанавливают корректирующую массу m_k на расстоянии е_k от оси вращения, и эта корректирующая масса создает дисбаланс:

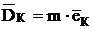
Для статического уравновешивания необходимо, чтобы

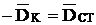
при этом можно задаться величиной m_k и определить е_k , или задаться е_k и найти m_k.

В результате уравновешивания главная центральная ось инерции должна совпасть с осью вращения.

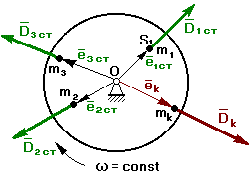Однако бывают случаи, когда в силу конструктивных особенностей ротора нельзя установить одну корректирующую массу. Тогда устанавливают две корректирующих масс в разных плоскостях.

Бывает другой случай статической неуравновешанности, когда ротор по своему объему имеет какие-либо включения сторонних предметов или частиц.

Каждая частица создает дисбаланс: D_ст1, D_ст2, D_ст3.

Возникает вопрос, как расположить корректирующую массу?

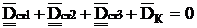
Строится план дисбалансов.

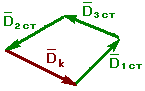
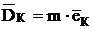
Величину и направление D_k определяют из плана.

Здесь также либо задаются величиной m_k и определяют е_k , либо задаются е_k и находят m_k.

3.2.2 Моментная неуравновешанность ротора и способы ее устранения.

Моментная неуравновешанность характеризуется тем, что центр масс ротора расположен на оси его вращения, главная центральная ось инерции повернута относительно оси вращения на некоторый угол g.

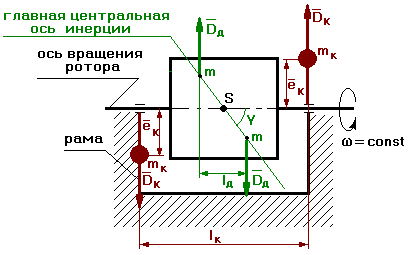
Моментная неуравно-вешанность проявляется только при вращении ротора (появляются биения на опорах).

Динамический момент, возникающий при вращении ротора

M_Д = D_Д^.l_Д

Для устранения моментной неуравновешанности выбирают в произвольном месте две корректирующие плоскости.

Выберем их так, чтобы одна проходила через опору А, другая – через опору В.

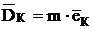в обоих плоскостях

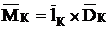
Для моментного уравновешивания необходимо чтобы

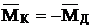
Таким образом, для устранения моментной неуравновешенности необходимо иметь две корректирующие массы, которые размещают в 2-х корректирующих плоскостях.

3.2.3 Динамическая неуравновешанность ротора и способы ее устранения.

Динамическая неуравновешанность является общим случаем неуравновешанности ротора, а именно имеет место как статическая, так и моментная неуравновешанности.

При этом центр масс ротора не лежит на оси вращения, и главная центральная ось инерции повернута на угол g относительно оси вращения.

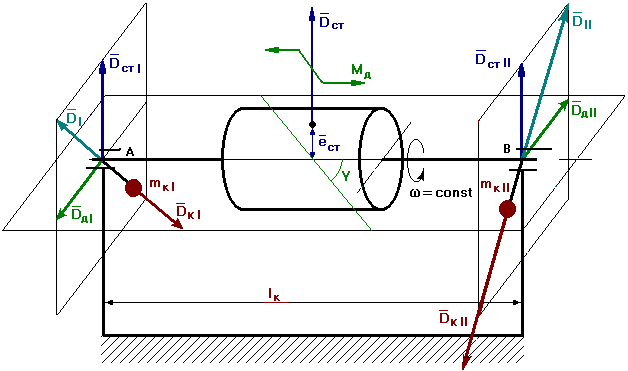
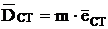
Выберем в произвольном месте две корректирующие плоскости (опоры А и В).

Вектор дисбаланса разнесем по этим плоскостям так, чтобы

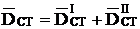
Динамический момент представим в виде пары сил

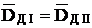M_Д = D_Д^.l_Д l_Д = l_АВ

Уравновешивание осуществляется в каждой плоскости отдельно (см. лаб. раб.№9).

В 1-ой плоскости находим результирующий вектор дисбаланса.

Для уравновешивания D_I необходимо на линии его действия установить корректирующую массу m_k1 на расстоянии е_к1 так, чтобы она создавала дисбаланс корректирующей массы в 1-ой плоскости

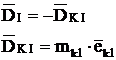
Во 2-ой плоскости

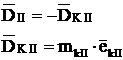
Динамическая неуравновешанность устраняется путем установки двух корректирующих масс в двух корректирующих плоскостях. При этом дисбалансы корректирующих масс в 1-ой и во 2-ой плоскостях неравны и непараллельны.

Глава4. Механизмы с высшей кинематической парой.

В этом разделе будут рассмотрены передаточные механизмы с высшей КП, а именно:

1. цилиндрические зубчатые передачи с эвольвентным профилем зубов и постоянным передаточным отношением;

2. планетарные механизмы с подвижными осями зубчатых колес.

Достоинство механизмов с высшей КП:

1. малые габариты и вес;

2. возможность точного воспроизведения закона движения выходного звена (по сравнению с рычажными механизмами зубчатые передачи имеют меньше зазоров);

3. высокий КПД (0,85 – зубчатая передача, 0,99 – планетарный механизм).

Недостатки:

наличие высшей КП может привести к повышенным удельным давлениям в точке контакта. Это в свою очередь может привести к выкрашиванию материалов (питтинг).

§4.1 Условие существования высшей КП.

Для того чтобы не было отрыва или внедрения поверхностей звеньев, образующих высшую КП, необходимо, чтобы проекции линейных скоростей взаимодействующих тел на общую нормаль, проведенную в точке контакта тел, были равны.

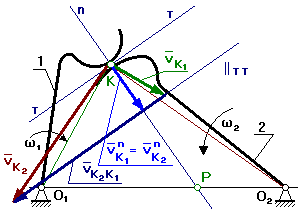
§4.2 Кинематика высшей КП.

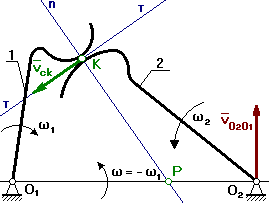
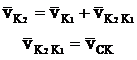
Для определения мгновенного центра скоростей тела 1 и тела 2 в относительном движении применим метод обращения движения, в соответствии с которым мысленно сообщим каждому из звеньев, включая стойку, дополнительное движение

рис. 4.4.1 с угловой скоростью -w₁.

Тогда в обращенном движении

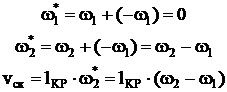
Для нахождения МЦС к относительным линейным скоростям V_O2O1 и V_ck восстанавливают перпендикуляры, на пересечении которых получают точку Р. – МЦС в относительном движении.

Точка Р. – полюс зацепления.

Если зацепляющиеся тела имеют наружные зубья, то полюс Р. расположен между осями О₁ и О₂ .

Если хотя бы одно из колес имеет внутренние зубья, то полюс Р расположен за линией О₁О₂.

ЛЕКЦИЯ 8.

Сопряженные поверхности – поверхности, которые постоянно или с определенной периодичностью входят в зацепление друг с другом.

По отношению к начальным окружностям сопряженные поверхности могут занимать различные положения. Правильным положением является то, которое удовлетворяет основной теореме зацепления, теореме о мгновенном передаточном отношении, которое формулируется:

Общая нормаль, проведенная в точке контакта сопряженных поверхностей, проходит через линию центров О₁О₂ и делит эту линию на части, обратно пропорциональные отношению угловых скоростей.

Передаточное отношение

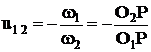(см рис. 4.4.1)

Сопряженные профили должны удовлетворять следующим требованиям:

1. быть простыми в изготовлении (технологичными);

2. иметь высокий КПД.

Таким требованиям удовлетворят эвольвентные профили.

§4.3 Эвольвента и ее свойства.

Эвольвента образуется путем перекатывания производящей прямой K_yN_y без скольжения по основной окружности радиуса r_b.

Радиус произвольной окружности – r_y. ON_y || tt

Из треугольника ON_yK_y следует, что

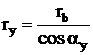(1)

Т.к. K_yN_y перекатывается без скольжения по основной окружности, то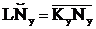

r_b(q_y + a_y) = r_b^.tg a_y

q_y = tg a_y - a_y (2)

q_y = inv a_y

q_y – инволюта;

Уравнения (1) И (2) являются уравнениями эвольвенты в параметрической форме.

a_у – угол профиля эвольвенты для точки К_у, лежащей на произвольной окружности.

a – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.

Угол профиля эвольвенты для точки К_b, лежащей на основной окружности, равен нулю: a_b=0.

Свойства эвольвенты.

1. Форма эвольвенты зависит от радиуса основной окружности. При стремлении r_b 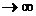,эвольвента превращается в прямую линию (пример рейка).

2. Производящая прямая K_yN_y является нормалью к эвольвенте в данной тоске.

3. Эвольвента начинается от основной окружности. Внутри основной окружности точек эвольвенты нет.

§4.4 Элементы эвольвентного зубчатого колеса.

Делительной окружностью называется окружность стандартных шага р, модуля m и угла профиля a.

Шаг – расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.

Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:

1 ряд – наиболее предпочтительный;

2 ряд – средней предпочтительности;

3 ряд – наименее предпочтительный.

Модуль характеризует высоту зуба. Чем больше зуб, тем более шумной становится зубчатая передача.

Угол профиля – угол между касательной к эвольвенте в данной точке и радиус-вектором данной точки (см. чертеж эвольвенты).

Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20^о(хотя лучше 25^о).

4.4.1 Основные расчетные зависимости для определения параметров эвольвентного зубчатого колеса.

Из (1) следует, что радиус делительной окружности

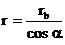
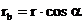(3)

модуль по ГОСТу определяется

m = p / p p = p^.m (4)

2p ^.r = p^.z

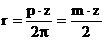(5)

2p ^.r_y = p_y^.z

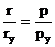à

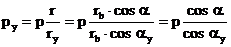
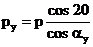(6)

по основной окружности

a_y = 0 à p_b = p cos 20^o (7)

4.4.2 Виды зубчатых колес.

p = s + e (8)

s= 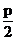+ Δ^.m (9)

где Δ – коэффициент изменения толщины зуба.

В зависимости от знака коэффициента Δ различают виды зубчатых колес:

1. Δ = 0 s = e = p/2 нулевое зубчатое колесо;

2. Δ > 0 s > e положительное зубчатое колесо;

3. Δ < 0 s < e отрицательное зубчатое колесо.

§4.5 Эвольвентная зубчатая передача и ее свойства (рис. 11-86).

Эвольвентную зубчатую передачу составляют, как минимум, из 2-х зубчатых колес, при этом в рассмотрение вводится две начальные окружности радиусами r_w1 и r_w2.

Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.

Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N₁N₂, которая одновременно касается 2-х основных окружностей r_b1 и r_b2.

Линия зацепления является геометрическим местом точек контакта сопряженных эвольвентных профилей. В точке В₁ пара эвольвент, которые в данный момент времени контактируют в точке К, входят в зацепление. В точке В₂ этаже пара эвольвент из зацепления выходят.

На линии зацепления N₁N₂ все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N₁N₂ эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.

Угол 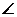N₁O₁P = 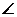N₂J₂P = a_w – угол зацепления.

Для передачи, составленной из нулевых зубчатых колес a_w=20^o

Для передачи, составленной из положительных з. к. a_w>20^o

Для передачи, составленной из отрицательных з. к. a_w<20^o

c=c*^.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.

c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).

Между делительными окружностями у^.m – это воспринимаемое смещение.

у – коэффициент воспринимаемого смещения, он имеет знак, и в зависимости от знака различают:

1. у=0 у^.m=0 – нулевая зубчатая передача;

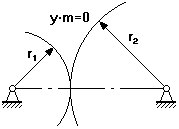
2. у>0 у^.m>0 – положительная зубчатая передача;

3. у<0 у^.m<0 – отрицательная зубчатая передача;

Свойства эвольвентного зацепления.

1. Эвольвентное зацепление молочувствительно к погрешностям изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное отношение зубчатой передачи не изменится.

2. Линия зацепления N₁N₂ является общей нормалью к сопряженным эвольвентным профилям.

3. Контакт эвольвент осуществляется только на линии зацепления.

ЛЕКЦИЯ 9.

4.5.1 Основные расчетные зависимости для определения основных параметров эвольвентных зубчатых передач.

1. Определение угла зацепления.

inv a_w = inv a + 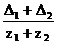(1)

где Δ_{1 ,} Δ₂ – изменение толщины зуба;

z₁ , z₂ – число зубьев.

2. Определение межосевого расстояния зубчатых передач.

а_w = r_w1 + r_w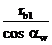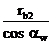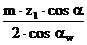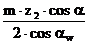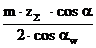2 = + = + = (2)

z_Σ = z₁ + z₂

3. Определение коэффициента воспринимаемого смещения y.

а_w = r₁ + r₂ + y m

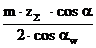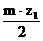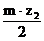= + + y m

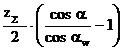y = (3)

4.5.2 Качественные показатели зубчатых передач.

к ним относятся:

1. Коэффициент перекрытия e_a.

Характеризует плавность работы зубчатой передачи и показывает, какое число зубьев одновременно участвуют в перекрытии зацепления (насколько одна пара зубьев перекрывает работу другой).

Теоретически e_a может равен 1, и это означает, что как только одна пара зубьев вышла из зацепления, следующая пара сразу же вошла в зацепление.

Если e_a<1, то предыдущая пара зубьев из зацепления вышла, а следующая пара в зацепление не вошла. Такая передача работает с ударами, и ее прим