Замена параллельных ветвей, содержащих источники ЭДС и тока, одной эквивалентной.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ДИСЦИПЛИНЕ
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
г. Волгодонск, 2015 г.
УДК 621.3.01
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ДИСЦИПЛИНЕ
«ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
Настоящие методические указания содержат рекомендации по решению и задания для выполнения контрольных работ по дисциплине «Теоретические основы электротехники». В начале разделов приводятся теоретические сведения, а так же примеры выполнения задач. / ВИТИ НИЯУ МИФИ. – Волгодонск, 2015. – 61 с.
© ВИТИ НИЯУ МИФИ, 2015
Содержание
Введение4
1 Задание №1. Цепи постоянного тока5
1.1 Теоретические положения7
1.2 Задача 118
1.3 Задача 221
1.4 Задача 323
1.5 Задача 425
2 Задание №2. Цепи однофазного синусоидального тока27
2.1 Теоретические положения27
2.2 Пример выполнения задания41
2.3 Задание на расчетно-графическую работу52
3 Расчет характеристик трехфазного трансформатора57
3.1 Методические указания к решению 3-ей задачи57
3.2 Задание на расчетно-графическую работу58
Список использованной литературы60
Введение
Данные методические указания предназначены для студентов очной и заочной формы обучения для выполнения контрольных работ по дисциплине «Теоретические основы электротехники».
Целью контрольной работы является ознакомление с основами электротехники и электроснабжения, изучение основных законов и методов упрощения электрических цепей и расчета их параметров.
Методические указания включают в себя 3 задания, а так же теоретические данные и примеры выполнения. Задания построены по вариантной схеме и состоят из таблиц вариантов и набора рисунков электрических цепей.
Задание №1. Цепи постоянного тока
Задачей расчета электрической цепи является определение токов в ее ветвях, потенциалов узлов, напряжений на отдельных участках (элементах) с последующей проверкой полученных результатов при помощи баланса мощностей. В процессе расчета часто применяют эквивалентные преобразования, которые заключаются в замене отдельных участков цепи более простыми. Замену осуществляют так, чтобы в остальной части цепи напряжения и токи не изменились. В результате эквивалентных преобразований упрощается исходная цепь и облегчается её расчет.
Электрической схемой называется графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов цепи.
Ветвью называется участок цепи, образованный одним или несколькими последовательно включенными элементами, по которым течет один и тот же ток.
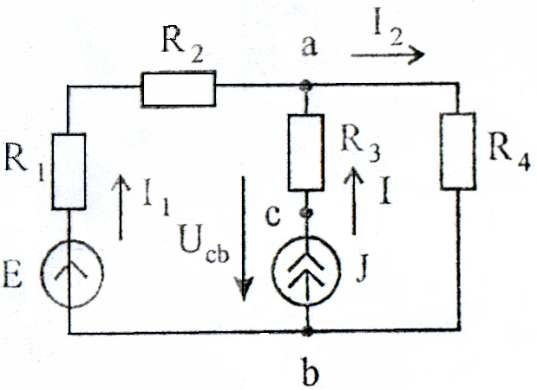
Рисунок 1
Так, в схеме (рисунок 1) три ветви. Первая образована элементами Е, R1, R2; вторая – R3, J; третья – одним сопротивлением R4. Узлом называется место соединения трех и более ветвей (точки "а" и "b" в схеме рисунок 1). Пассивными называются ветви, не содержащие источников электрической энергии. Пример пассивного элемента – электрическое сопротивление R, в котором происходит преобразование электрической энергии в тепловую.
Ветви, содержащие источники энергии, называются активными. Источниками электрической энергии являются генерирующие устройства, в которых энергия того или иного вида преобразуется в электрическую. В процессе расчета электрических цепей пользуются идеальными и реальными источниками ЭДС и тока.
Идеальным источником ЭДС (рисунок 2) называется активный элемент с двумя выводами, напряжение на зажимах которого не зависит от тока, протекающего через источник, т. е Uab = Е.
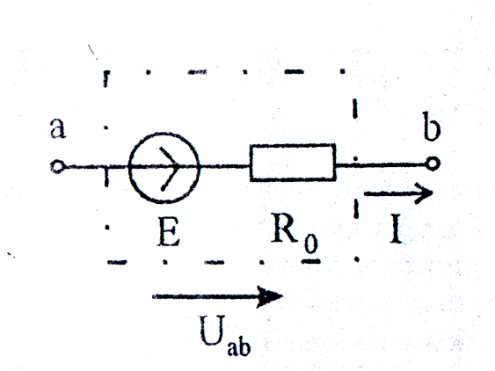
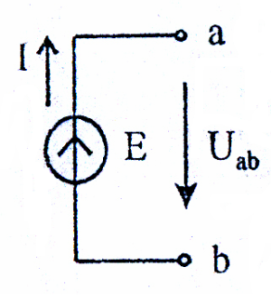
Идеальный источник ЭДС является источником бесконечной мощности, его внутреннее сопротивление равно нулю. Стрелка внутри источника указывает на направление возрастания потенциала. У реального источника ЭДС конечной мощности (рисунок 3) внутреннее сопротивление R0 не равно нулю. При увеличении тока, отдаваемого в нагрузку, происходит уменьшение напряжения Uab.
Рисунок 2 Рисунок 3
Идеальным источником тока (рисунок 4) называется активный элемент с двумя выводами, ток которого не зависит от напряжения Uab на его зажимах. Идеальный источник является источником бесконечной мощности. Его внутренняя проводимость равна нулю, а внутреннее сопротивление – бесконечно велико. Схема замещения реального источника тока конечной мощности приведена на рисунке 5
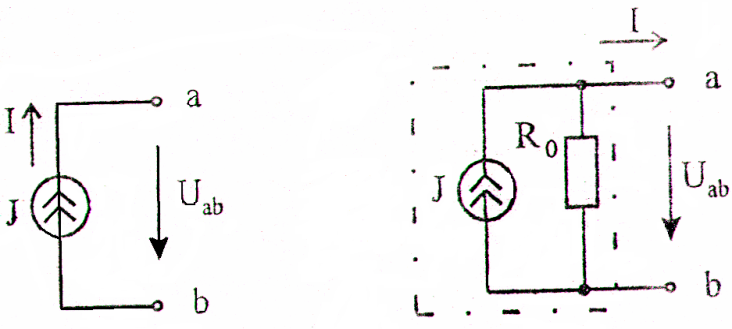
Рисунок 4 Рисунок 5
Теоретические положения
Закон Ома
Ток I и напряжение U на сопротивлении R связаны законом Ома следующим образом:
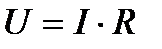
Законы Кирхгофа
Электрические цепи постоянного тока могут быть рассчитаны с помощью законов Кирхгофа.
Первый закон Кирхгофа:
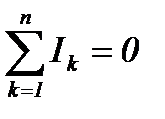
Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, направленные к узлу, условно принимаются положительными, а направленные от него – отрицательными (или наоборот).
Второй закон Кирхгофа:
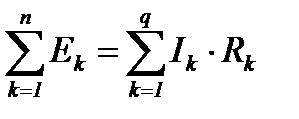
Алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений в нём. Направление обхода контура выбирается произвольно; при записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода, принимаются положительными, а ЭДС, направленные против выбранного обхода – отрицательными. При записи правой части со знаком "+" берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода, и со знаком " – " падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода. Если цепь содержит Nв – ветвей, Nу – узлов, Nт – источников тока, то:
1) устанавливается число неизвестных токов: Nв - Nт;
2) число линейно-независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы: Nу - 1;
3) число уравнений, составляемых по второму закону Кирхгофа:
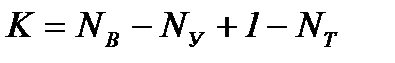
При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры (каждый из которых содержит по сравнению с предыдущим хотя бы одну новую ветвь), не содержащие источников тока. Так, для цепи Рисунок 1 система уравнений имеет вид:
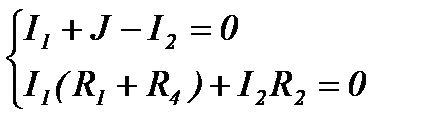
Баланс мощностей
Пусть в электрической цепи имеются источники и приемники электрической энергии. Тогда условие баланса мощностей, являясь следствием закона сохранения энергии, формулируется следующим образом: суммарная мощность, генерируемая источниками энергии, равна суммарной мощности, потребляемой в цепи:
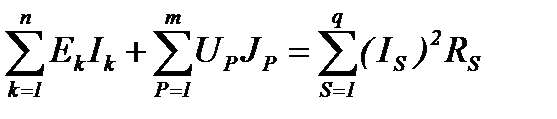
Где n – число ветвей, содержащих источники ЭДС;
m – число ветвей, содержащих источники тока;
UP – напряжение на зажимах источника тока;
q – число ветвей, содержащих сопротивления.
Мощность источника может быть положительной (если направления тока совпадает с направлением ЭДС Ek или напряжения UP) или отрицательной (направления тока и ЭДС противоположны или UP отрицательно). Отрицательный знак мощности означает, что соответствующий источник работает в режиме потребления энергии.
Так для цепи (рисунок 1) баланс мощностей имеет вид
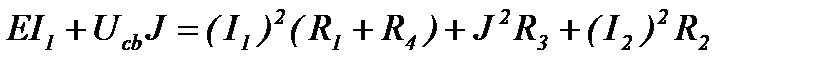
1.1.4 Преобразование пассивных ветвей
Замена последовательно соединенных сопротивлений одним эквивалентным.Сопротивления соединены последовательно, если они обтекаются одним током (рисунок 6).

Рисунок 6
Эквивалентное сопротивление цепи, состоящее изn последовательно соединенных сопротивлений, равно сумме этих сопротивлений, т.е.
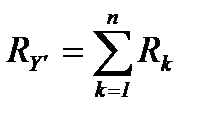
Замена параллельных сопротивлений одним эквивалентным.Сопротивления параллельны, если все они присоединены к одной паре узлов (рисунок 7).
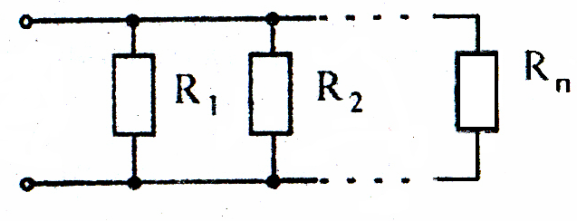
Рисунок 7
Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных сопротивлений, есть величина, обратная сумме проводимостей отдельных ветвей.
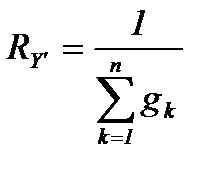 ,
, 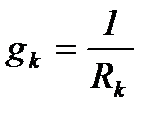
где 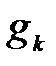 – проводимость k – й ветви.
– проводимость k – й ветви.
В частном случае параллельного соединения двух и трех сопротивлений (рисунок 8) соответственно эквивалентные сопротивления:
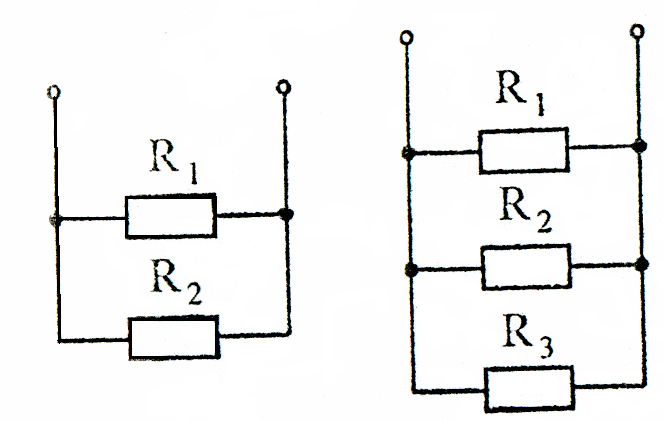
Рисунок 8
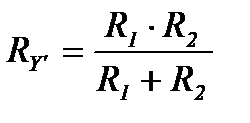 ;
; 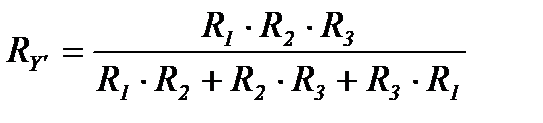
Замена смешанного соединения одним эквивалентным.Смешанное соединение – сочетание последовательного и параллельного соединений сопротивлений (рисунок 9):
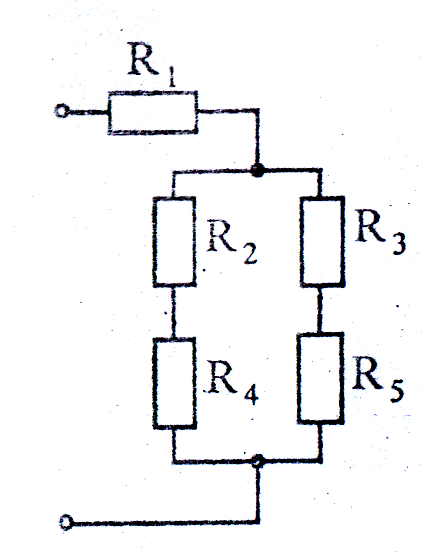
Рисунок 9
Пример 1. 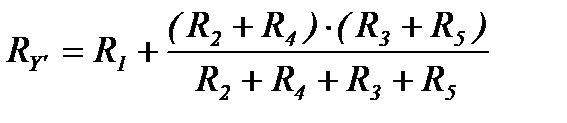
Определить эквивалентное сопротивление цепи (рисунок 10а) между точками а и b при разомкнутом и замкнутом ключе. Дано: R1 = R2 = R3 = R4 = R5 = R6 = R7 = 10 Ом.
Решение
Заданная цепь при разомкнутом ключе изображена на рис.10 б.
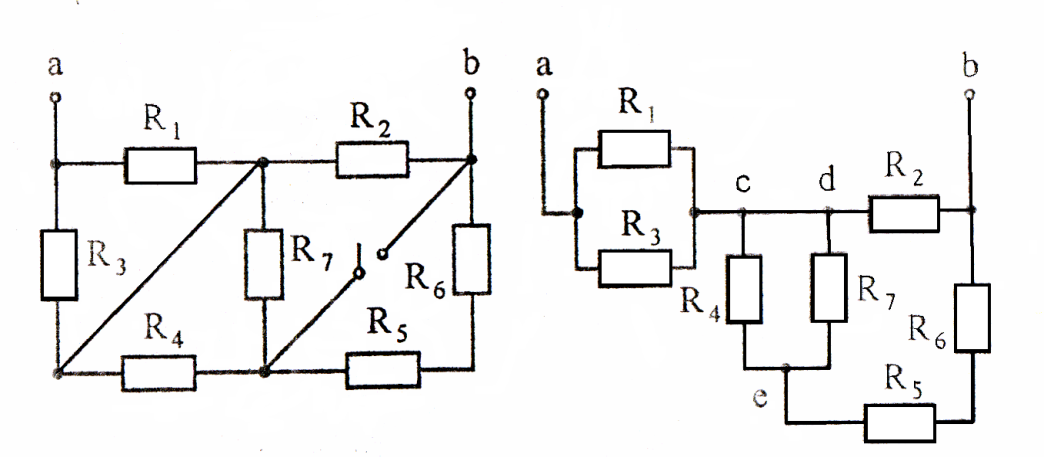
а) б)
Рисунок 10
Искомое сопротивление определяем следующим образом:
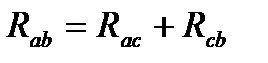 ;
;
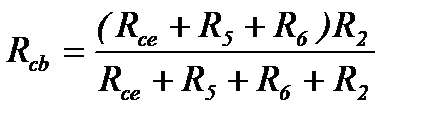 ;
;
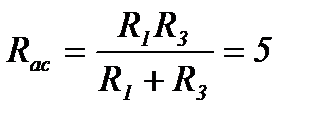 Ом;
Ом;
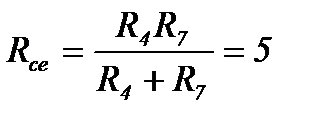 Ом;
Ом;
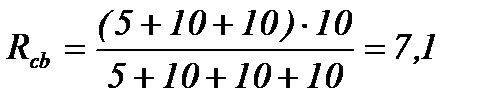 Ом;
Ом;
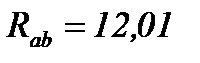 Ом.
Ом.
При замкнутом ключе схема имеет вид, изображенный на рисунке 11.
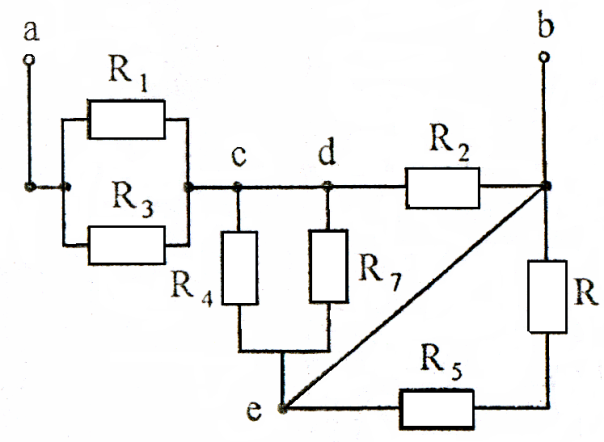
Рисунок 11
Сопротивление цепи равно сумме двух сопротивлений, а именно:
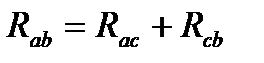 ;
;
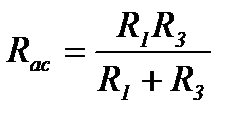 ;
;
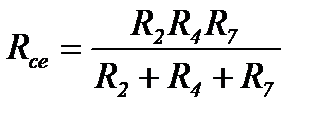 ;
;
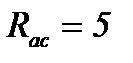 Ом,
Ом, 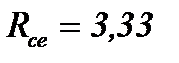 Ом,
Ом, 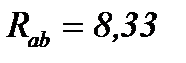 Ом.
Ом.
Формулы преобразования треугольника сопротивлений в эквивалентную звезду и наоборот (рисунок 12)
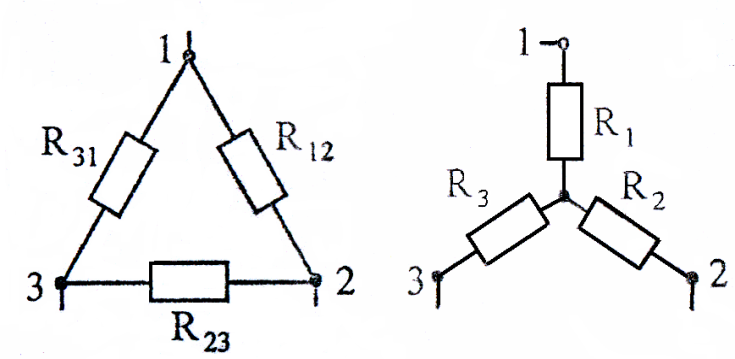
Рисунок 12
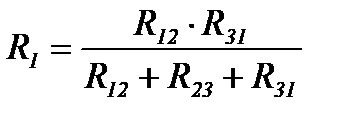 (1)
(1)
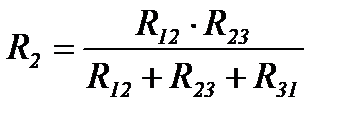 (2)
(2)
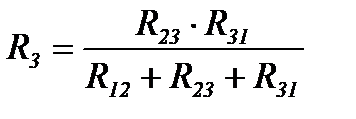 (3)
(3)
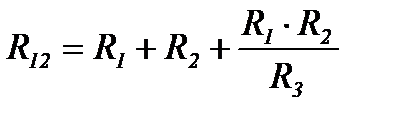 (4)
(4)
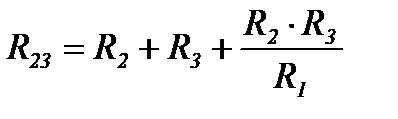 (5)
(5)
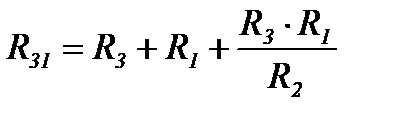 (6)
(6)
1.1.5 Преобразование активных ветвей
Замена ветви с несколькими источниками ЭДС ветвью с одной эквивалентной ЭДС. Условиями эквивалентности является равенство напряжений на зажимах (Uab, рисунок 13) исходной и эквивалентной ветвей, а также токов в ветвях.
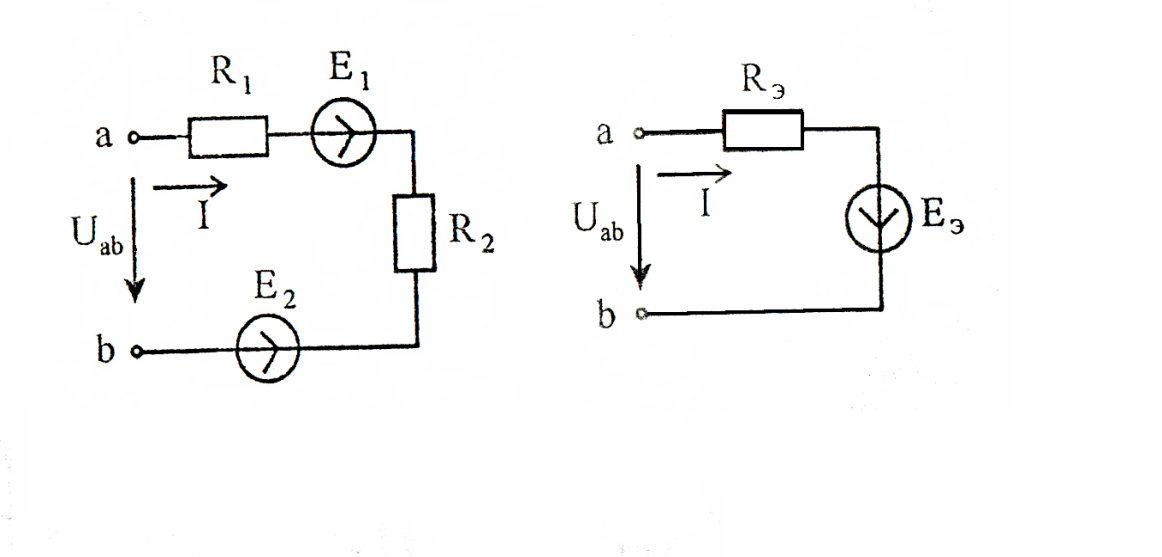
Рисунок 13
Величины ЕЭ, RЭ можно определить с помощью второго закона Кирхгофа. Так, для исходной ветви (рисунок 13)
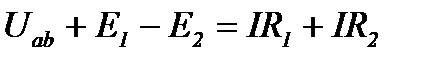 (7)
(7)
для эквивалентной ветви
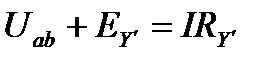 (8)
(8)
Сравнивая выражения (7) и (8), получим
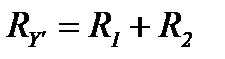 ;
; 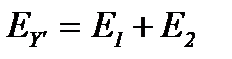 (9)
(9)
Формула (9) получена с учетом того, что направление эквивалентной ЭДС выбрано совпадающим с направлением тока в цепи. Отсюда следует простое правило расчета ЕЭ: если направление ЭДС источника в исходной цепи (E1, рисунок 13) совпадает с направлением тока, то она входит в правую часть формулы (9) со знаком плюс, иначе – минус (Е2, рисунок 13).
Задача 1
Определить эквивалентное сопротивление RЭ (рисунок 20, 21, 22) относительно указанных зажимов, если сопротивления равны 10 Ом. Данные взять из табл. 1-3 (номер варианта соответствует порядковому номеру студента в журнале).
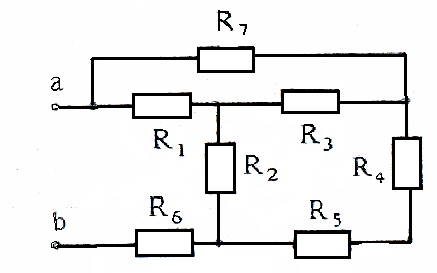
Рисунок 20
Таблица 1.
| № | ||||||||||
| R7=0 | R4=∞ | R3=∞ | R1=0 | R1=∞ | R2=0 | R2=∞ | R7=0 | R4=0 R5=0 | R7=∞ | |
| № | ||||||||||
| R3=0 | R4=0 | R5=∞ | R6=0 | R1=∞ | R2=0 R6=0 | R2=∞ R1=0 | R7=0 R2=∞ | R4=0 R5=0 | R7=∞ |
Таблица 1
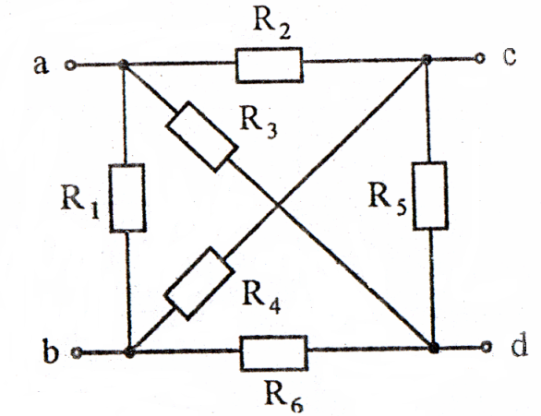
Рисунок 21
Таблица 2
| № | ||||||||||
| R5=0 | R5=∞ | R4=0 | R3=0 | R3=0 | R1=∞ | R5=0 | R2=0 | R4=0 | R2=0 | |
| Rab | Rab | Rab | Rcd | Rac | Rbd | Rac | Rcd | Rad | Rbc | |
| № | ||||||||||
| R3=∞ | R4=0 R6=∞ | R6=∞ | R6=0 | R1=∞ | R2=0 R6=0 | R2=∞ R1=0 | R7=0 R2=∞ | R4=0 R5=0 | R5=∞ R1=0 | |
| Rac | Rbd | Rac | Rcd | Rad | Rbc | Rab | Rab | Rab | Rcd |
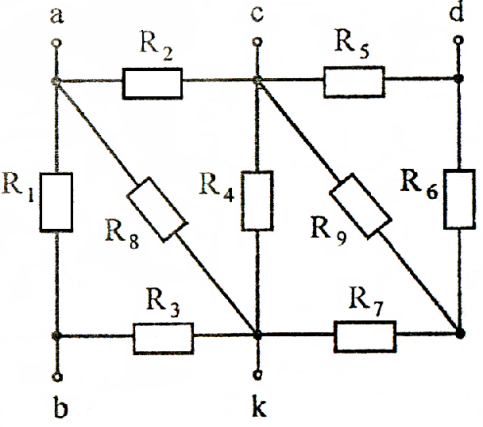
Рисунок 22
Таблица 3
| № | ||||||||||
| R9=0 | R4=∞ | R7=∞ | R8=0 | R8=0 R9=0 | R8=0 R9=∞ | R8=0 | R2=0 R7=0 | R6=∞ | R3=∞ R8=0 | |
| Rab | Rab | Rab | Rcd | Rac | Rkd | Rcd | Rcb | Rck | Rak | |
| № | ||||||||||
| R8=0 | R8=0 R9=0 | R8=0 R9=∞ | R8=0 | R2=0 R7=0 | R6=∞ | R3=∞ R8=0 | R9=0 | R4=∞ | R7=∞ | |
| Rab | Rab | Rab | Rcd | Rac | Rkd | Rcd | Rcb | Rck | Rak |
Задача 2
Используя преобразования параллельных ветвей, упростить схему до трёхконтурной. Составить уравнения по законам Кирхгофа для эквивалентной схемы. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема, 12 – 2 схема, и т.д.).
Схемы к задаче 2:
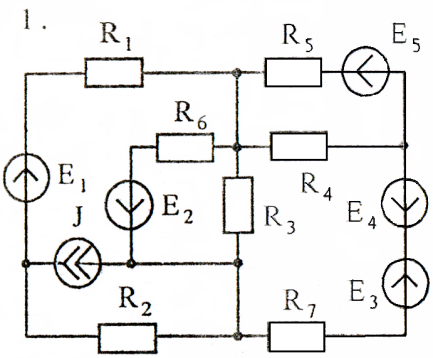
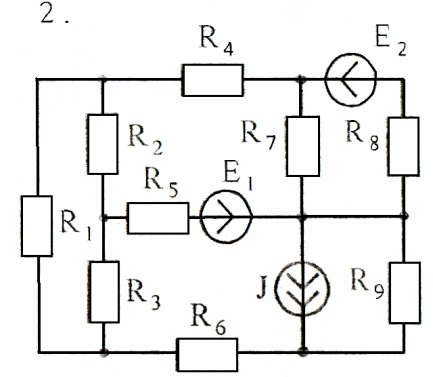
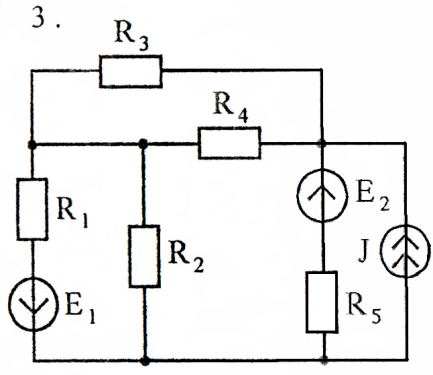
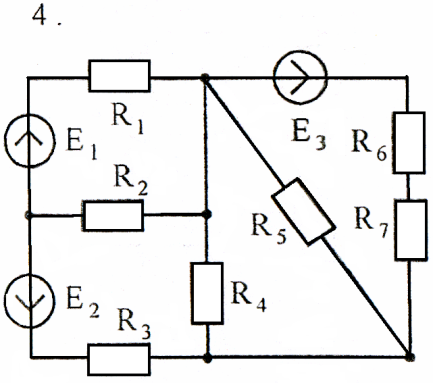
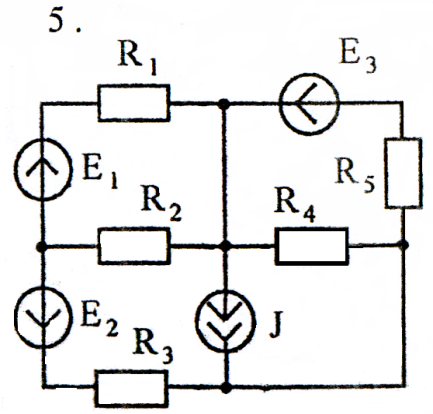
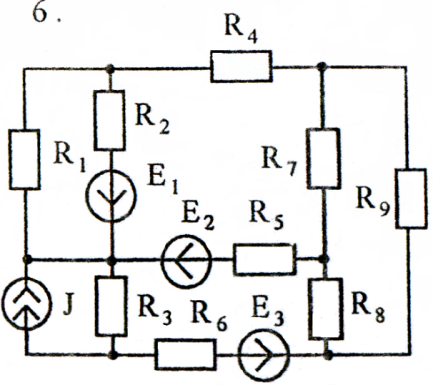
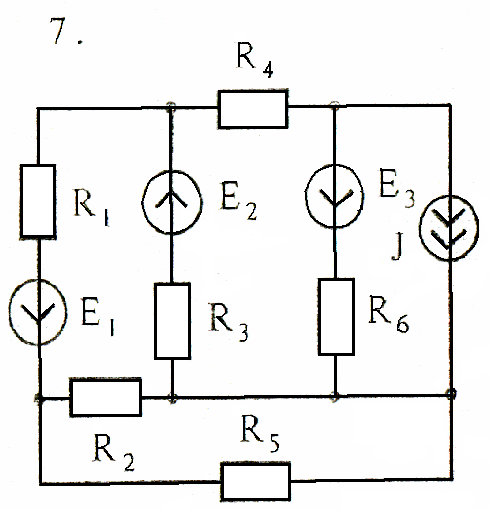
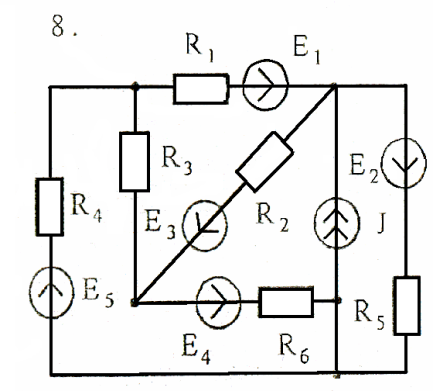
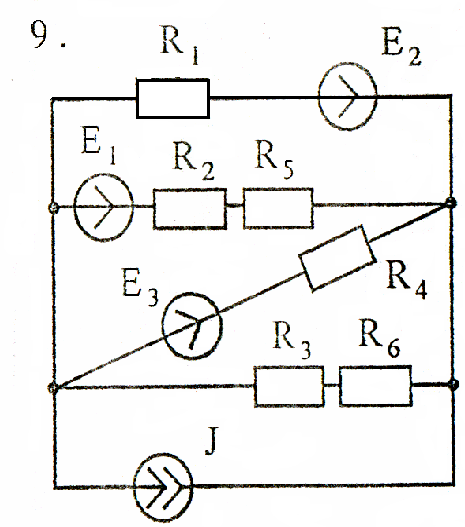
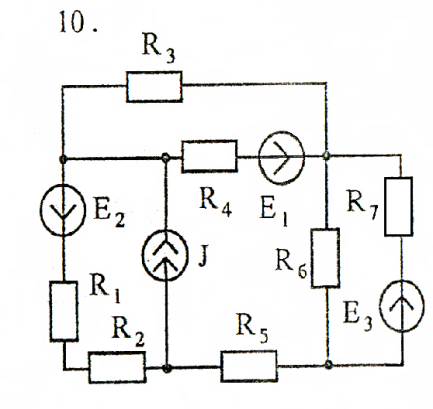
Задача 3
Используя взаимные преобразования активных треугольника и звезды, упростить схему до трёхконтурной. Номер схемы соответствует порядковому номеру студента в журнале (номеру 11 соответствует 1 схема, 12 – 2 схема, и т.д.).
Схемы к задаче 3:
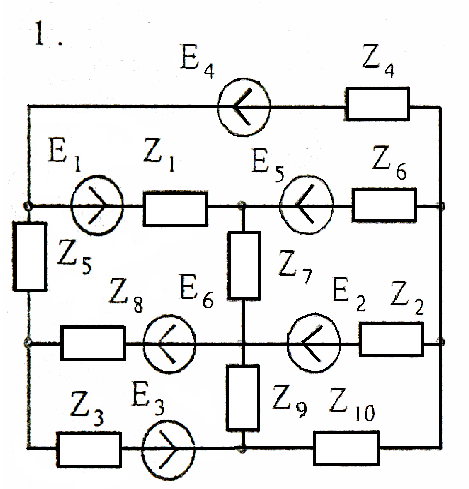
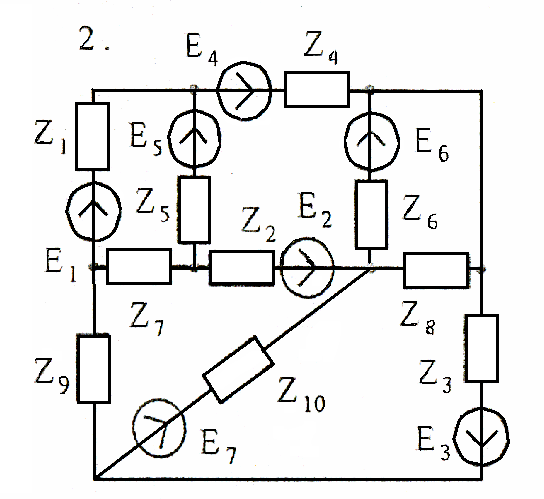
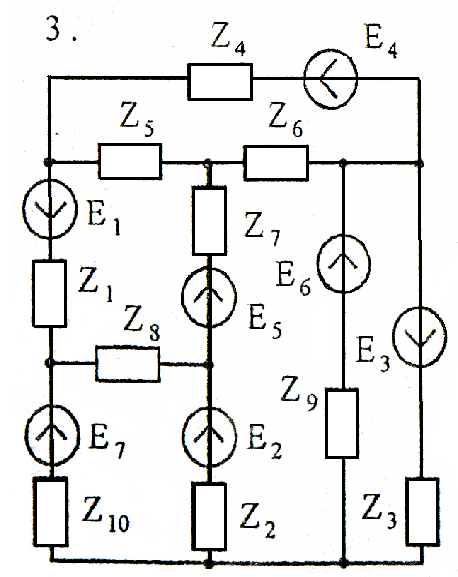
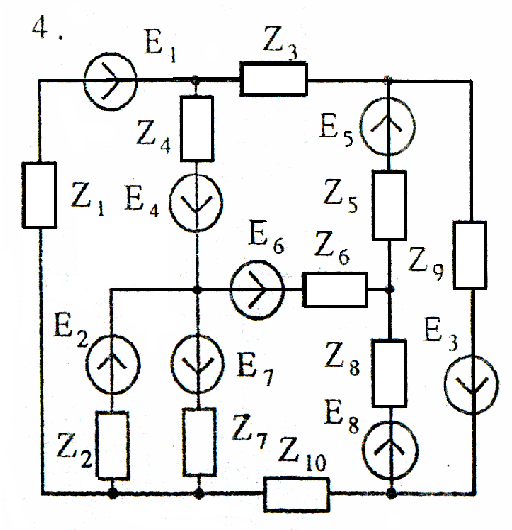
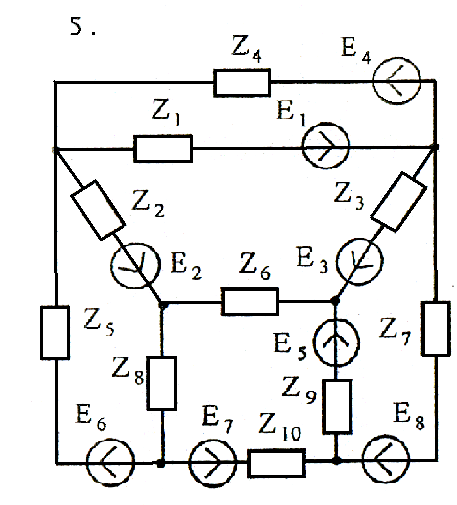
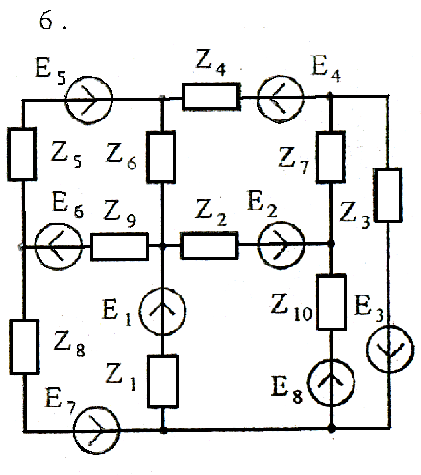
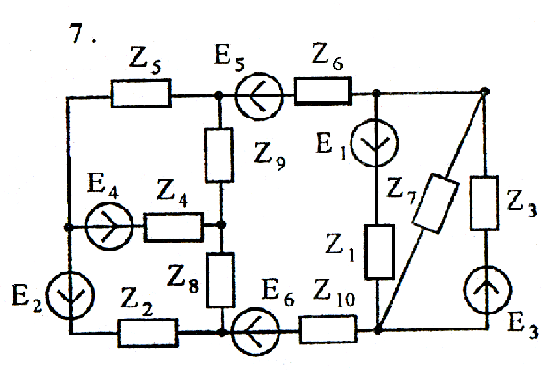
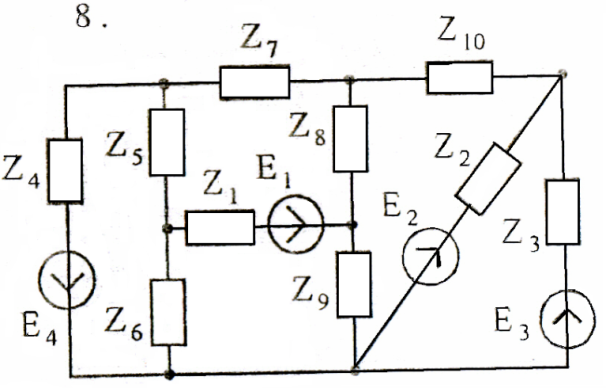
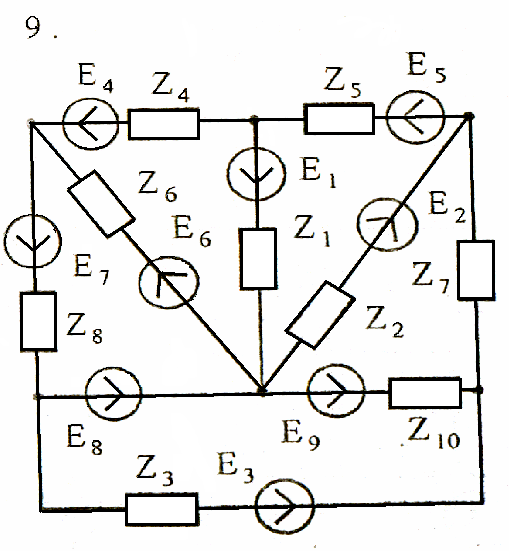
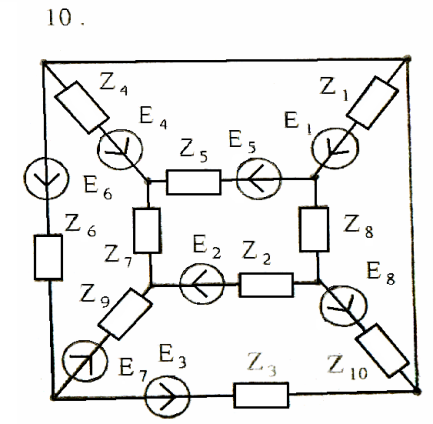
Задача 4
В цепи (рисунок 23) три источника питания, ЭДС которых равны E1,E2,E3; их внутренние сопротивления соответственно равны R01 = 0,1 Ом; R02 = 0,2 Ом; R03 = 0, 3 Ом. Отдельные ветви цепи могут быть разомкнуты при помощи рубильников P1, P2, P3, P4, P5, P6. Сопротивления в пассивных ветвях R1 = 1,5 Ом; R2 = 21 Ом; R3 = 2,5 Ом; R4 = 2 Ом; R5 = R6 = R7 = R8 = 3 Ом. Определить по методу непосредственного применения законов Кирхгофа токи во всех ветвях и режимы работы источников энергии. Составить баланс мощностей. Данные взять из табл. 4 (номер варианта соответствует порядковому номеру студента в журнале, номеру 11 соответствует 1 вариант, 12 – 2 вариант, и т.д.).
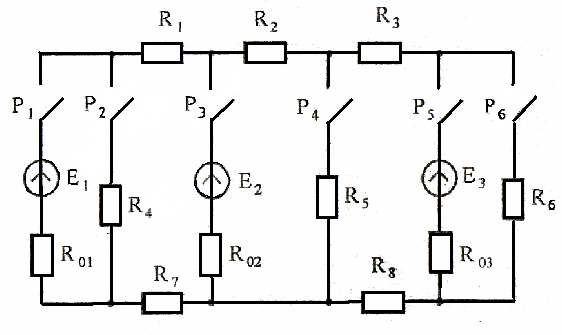
Рисунок 23
Таблица 4
| Вариант | Данные к задаче 4 | |||
| E1,В | E2,В | E3,В | Разомкнуты рубильники | |
| P4,P5,P6 | ||||
| P2,P5,P6 | ||||
| P2,P4,P5 | ||||
| P1,P4,P6 | ||||
| P2,P3,P6 | ||||
| P4,P5,P6 | ||||
| P2,P4,P5 | ||||
| P2,P3,P6 | ||||
| P1,P4,P6 | ||||
| P2,P5,P6 | ||||
| P4,P5,P6 | ||||
| P2,P5,P6 | ||||
| P2,P4,P5 | ||||
| P1,P4,P6 | ||||
| P2,P3,P6 | ||||
| P2,P3,P6 | ||||
| P1,P4,P6 | ||||
| P2,P5,P6 | ||||
| P4,P5,P6 | ||||
| P2,P5,P6 |
Задание №2. Цепи однофазного синусоидального тока
Задачей расчёта электрической цепи является определение токов в её ветвях, напряжений на участках цепи или потенциалов узлов. При этом задаются: конфигурация цепи, параметры ее элементов и ЭДС, источников. Для расчёта токов в сложных электрических цепях применяются методы уравнений Кирхгофа, контурных токов, узловых потенциалов, эквивалентного генератора.
Теоретические положения
Метод уравнений Кирхгофа
Расчёт линейных электрических цепей методом законов Кирхгофа сводится к решению систем алгебраических уравнений относительно неизвестных токов. Так как число неизвестных токов в заданной схеме равно числу ветвей n этой схемы, то система алгебраических уравнений должна иметь n-й порядок.
Пусть k – число узлов схемы. Из принципа непрерывности токов следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k-1).Недостающие уравнения, число которых [n-(k-1)], составляются по второму закону Кирхгофа для независимых контуров, не содержащих источников тока. Контуры являются независимыми, если в каждый из них входит ветвь, не входящая во все остальные.
Рассмотрим на примере расчёт токов в схеме (рисунок 24), которая содержит 6 ветвей, 4 узла и 3 независимых контура. Выберем произвольно направление токов в ветвях и направление обхода независимых контуров. Первые три уравнения (4 - 1 = 3) запишем по первому закону Кирхгофа, а оставшиеся три (6 - 3 = 3) – по второму закону Кирхгофа:
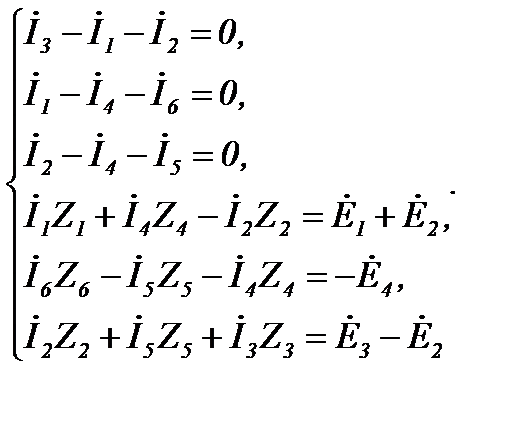
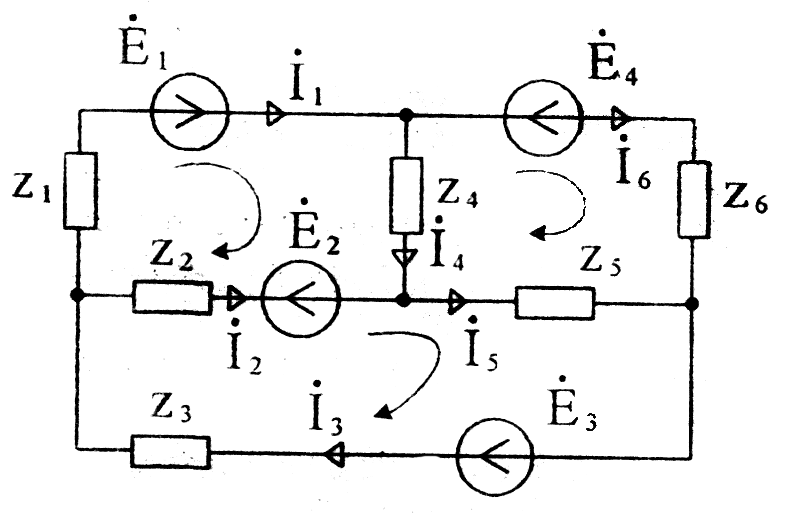
Рисунок 24
Решение полученной системы уравнений дает искомые токи. Если цепь содержит m ветвей с источниками тока, то число неизвестных токов уменьшается до (n-m). По первому закону Кирхгофа число уравнений остается без изменений (k-1), а по второму закону Кирхгофа она соответственно уменьшается на число ветвей с источниками тока [n-(k-1)-m].
Так, для схемы Рисунок 25, содержащей 6 ветвей и один источник тока, необходимо составить три уравнения по первому закону Кирхгофа и два – по второму.
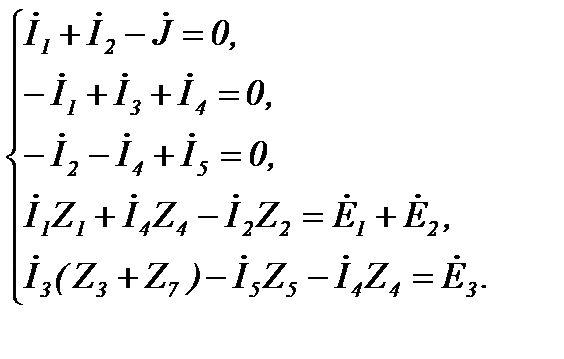
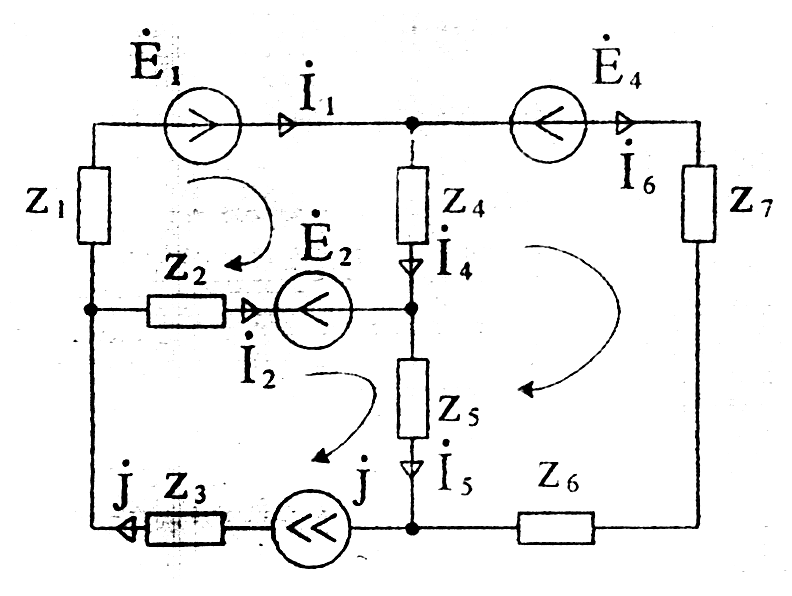
Рисунок 25
Если в результате расчётов какой-либо ток получился отрицательным, это значит, что его действительное направление противоположно выбранному.
К недостатку рассмотренного метода следует отнести высокий порядок системы уравнений для расчёта сложных электрических цепей.
Метод контурных токов
Расчёт разветвлённой цепи может быть сведён к решению всего [n-(k-1)] уравнений, составленных по второму закону Кирхгофа. Для этого цепь рассматривается как совокупность независимых соприкасающихся контуров и производится условная замена неизвестных токов в ветвях на токи, протекающие по замкнутым контурам. В уравнения, составленные по второму закону Кирхгофа, вводятся токи в независимых контурах – контурные токи.
Действительные токи в ветвях, принадлежащих только одному контуру, равны соответствующим контурным токам (но могут отличаться от них по направлению). Токи в общих для двух или нескольких контуров ветвях определяются как алгебраическая сумма соответствующих контурных токов. Первый закон Кирхгофа при этом будет выполняться автоматически. Направление контурных токов выбирается произвольно, а обход контуров условимся проводить в направлении контурных токов.
Для цепи с источниками ЭДС система уравнений, составленных для независимых контуров по второму закону Кирхгофа, содержит уравнения типа
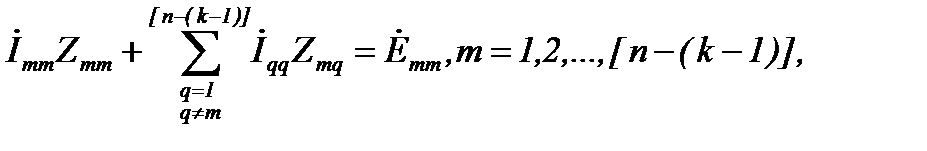
где 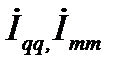 – контурные токи;
– контурные токи;
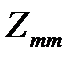 – сумма сопротивлений ветвей, образующих независимый m-й контур (контурное сопротивление),
– сумма сопротивлений ветвей, образующих независимый m-й контур (контурное сопротивление), 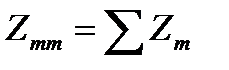 ;
;
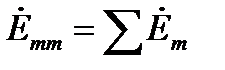 – сумма ЭДС этого контура;
– сумма ЭДС этого контура;
Zmq – сопротивление ветви, общей для m-го и q-контура (сопротивление связи).
Если в общих (смежных) ветвях направления контурных токов совпадают, то сопротивление связи берётся положительным, если токи направлены встречно, то – отрицательным. Контурные сопротивления всегда принимаются положительными.
При записи правой части уравнений ЭДС, направления которых совпадают с принятым направлением контурного тока (обхода), принимаются положительными, а при направленных противоположно – отрицательными.
Запишем систему уравнений по методу контурных токов для схемы Рисунок 26:
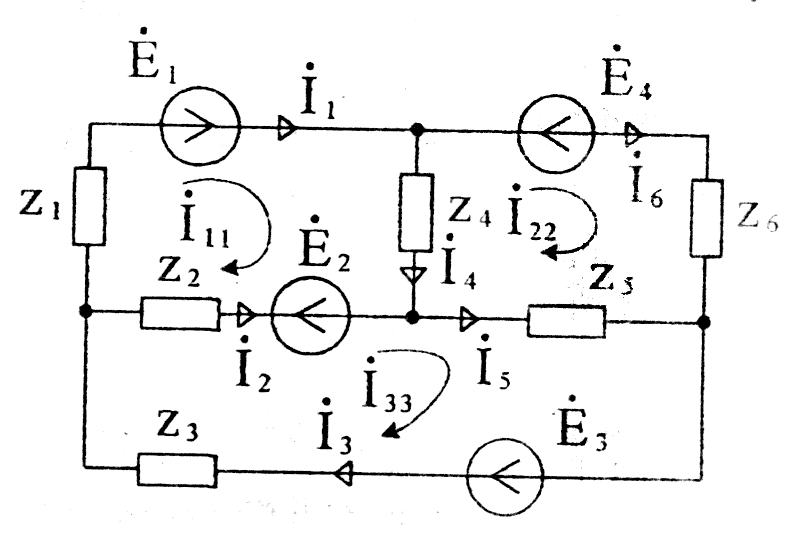
Рисунок 26
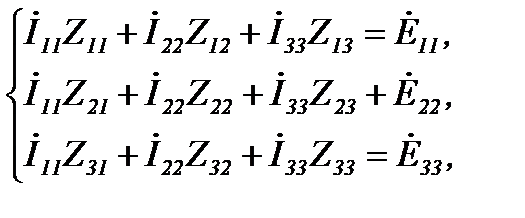
где
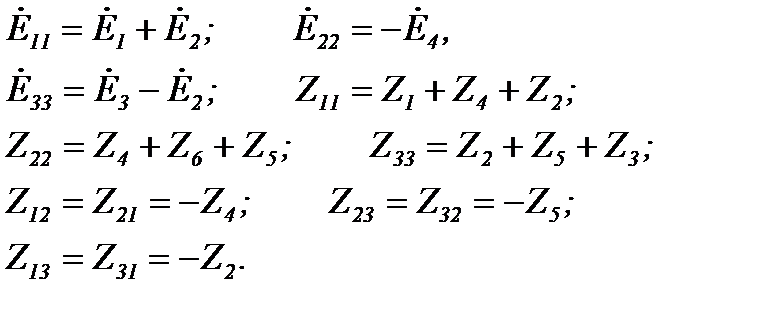
После решения системы уравнений относительно контурных токов находим токи в ветвях:
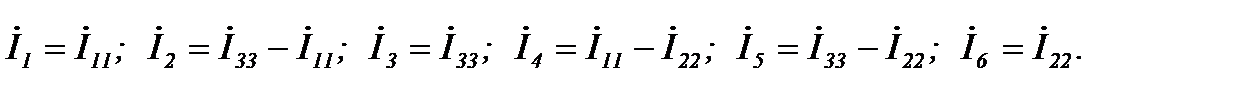 При наличии ветви с источником тока выбирается дополнительный контур, включающий эту цепь. Уравнение для дополнительного контура не составляется, т.к. контурный ток равен току источника. Падения напряжения на сопротивлениях связи с другими от источника тока (контурного тока) учитываются. Так, для цепи (рисунок 27) система уравнений имеет вид
При наличии ветви с источником тока выбирается дополнительный контур, включающий эту цепь. Уравнение для дополнительного контура не составляется, т.к. контурный ток равен току источника. Падения напряжения на сопротивлениях связи с другими от источника тока (контурного тока) учитываются. Так, для цепи (рисунок 27) система уравнений имеет вид
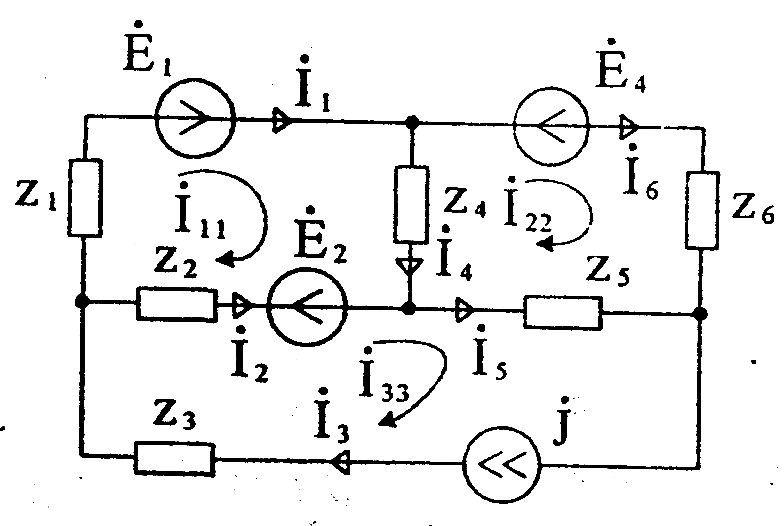
Рисунок 27
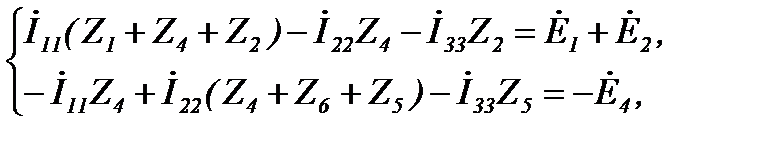
где. 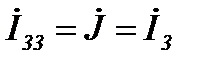
Метод узловых потенциалов
Если в разветвлённой электрической цепи число узловбез единицы меньше, чем число независимых контуров (k-1)<[n-(k-1)], удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы алгебраических уравнений (k-1)-го порядка относительно неизвестных потенциалов (узловых потенциалов). При этом потенциал одного из узлов схемы полагают равным нулю.
Уравнения с узловыми потенциалами вытекают из первого закона Кирхгофа. После нахождения неизвестных потенциалов определяют токи в ветвях по закону Ома.
Уравнения, входящие в систему, являются однотипными и для m-го узла имеют следующий вид:
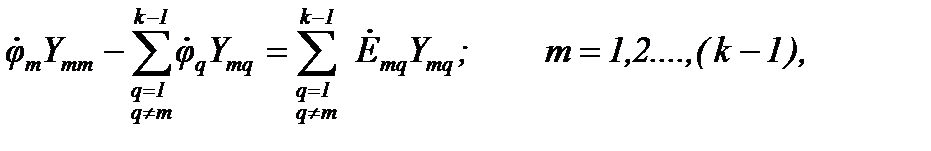
где 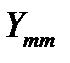 – сумма проводимостей всех ветвей, сходящихся в m-ом узле,
– сумма проводимостей всех ветвей, сходящихся в m-ом узле, 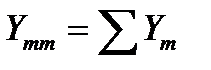 ;
;
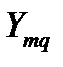 – проводимость ветви, соединяющей узел m c узлом q. Если между какими-либо узлами нет ветви, то соответствующая проводимость равна нулю;
– проводимость ветви, соединяющей узел m c узлом q. Если между какими-либо узлами нет ветви, то соответствующая проводимость равна нулю;
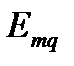 – ЭДС источников, расположенных в ветви между узлами m или q.
– ЭДС источников, расположенных в ветви между узлами m или q.
При этом ЭДС, направленные к узлу m (относительно которого составляется уравнение), берутся положительными, а направленные от этого узла – отрицательными.
Составим систему уравнений для схемы Рисунок 28, полагая 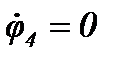 :
:
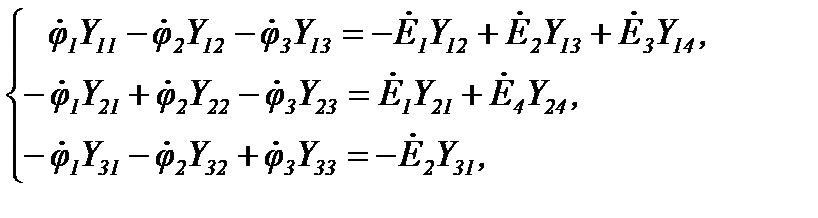
где
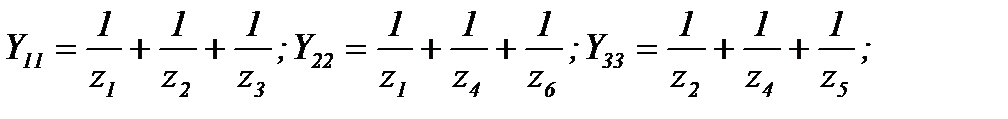
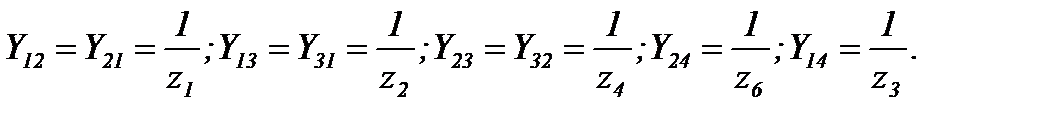
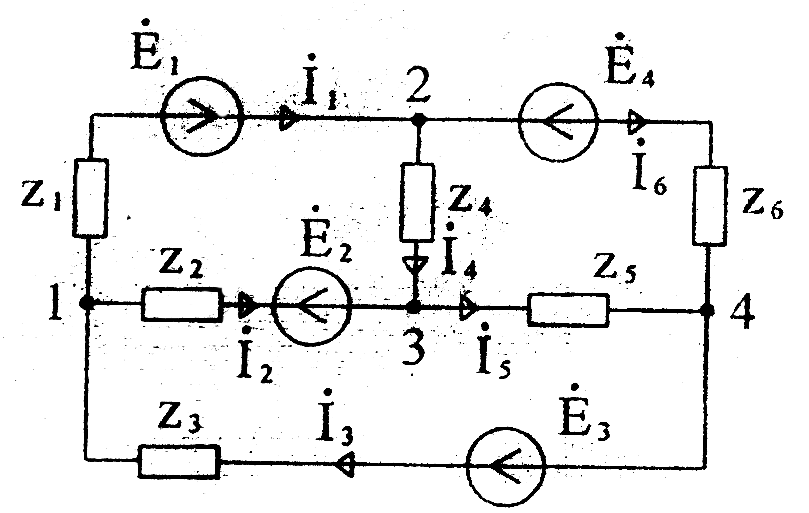
Рисунок 28
После определения потенциалов находим токи по закону Ома:
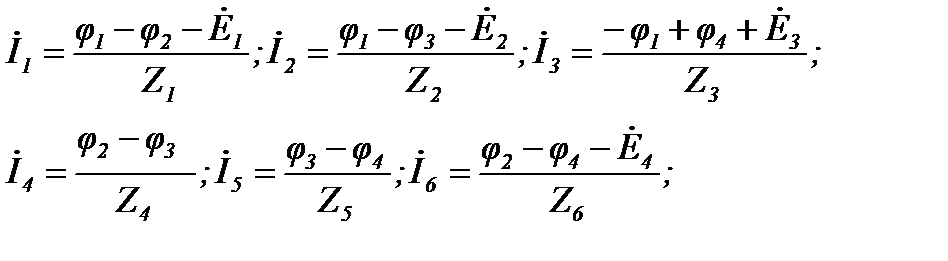
Если ветвь содержит источник тока, то её проводимость равна нулю, т.к. внутреннее сопротивление источника тока равно бесконечности. Если к m-му узлу подтекает ток от источника тока, то он должен быть включен в правую часть уравнения со знаком «плюс», если утекает, то со знаком «минус». Так, для цепи (рисунок 29) система уравнений имеет вид при 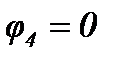 :
:
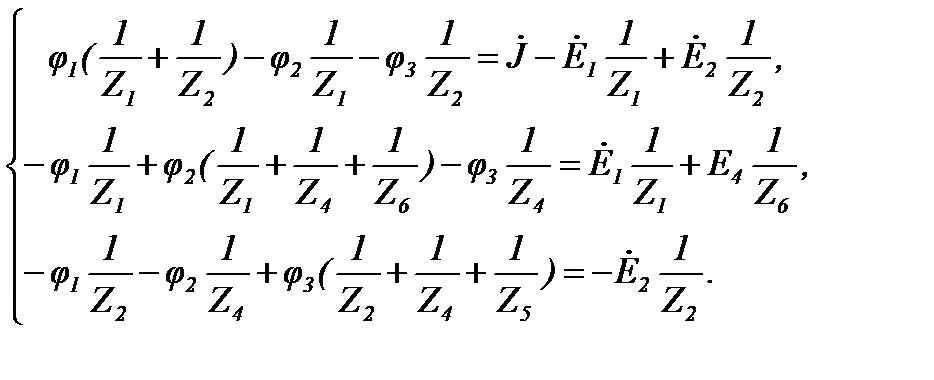
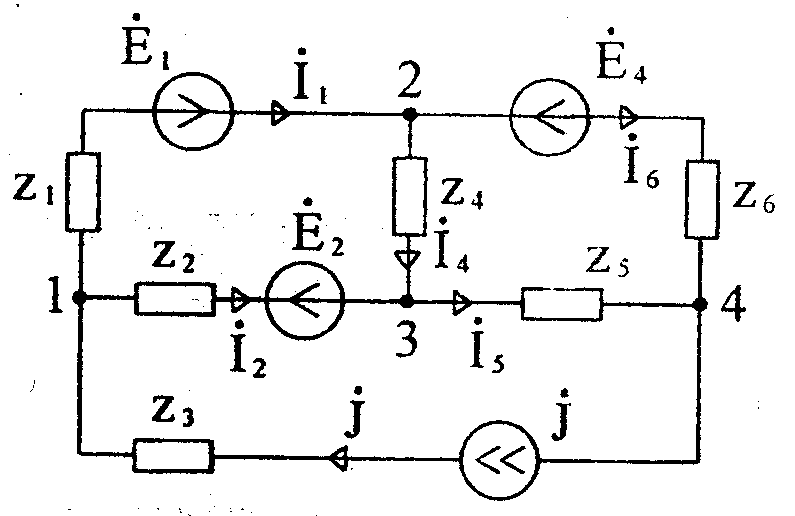
Рисунок 29
Баланс мощностей
В любой электрической цепи по закону сохранения энергии количество вырабатываемой за единицу времени энергии источников должно равняться мощности потребителей:
Рист=Рпотр, Qист=Qпотр.
Любое нарушение этих соотношений указывает на неточность проведённых вычислений.
Активную и реактивную мощности источников можно найти как действительную и мнимую части полной комплексной мощности источников:
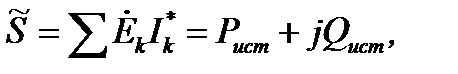
где 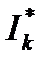 – сопряженный комплекс тока
– сопряженный комплекс тока 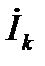
Если направление тока совпадает с направлением источника ЭДС, то произведение 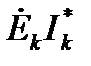 входит в левую часть равенства со знаком «плюс», в противном случае – со знаком «минус».
входит в левую часть равенства со знаком «плюс», в противном случае – со знаком «минус».
Если электрическая цепь содержит источник тока j, то
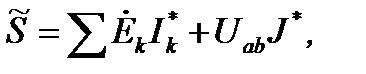
где 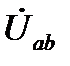 – напряжение на зажимах источника тока.
– напряжение на зажимах источника тока.
Активная мощность потребителей:
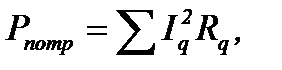
где Iq – действующее значение тока q-й ветви, содержащей активное сопротивление Rq.
Реактивная мощность потребителей:
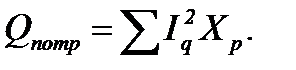
Для индуктивности произведение I2XL входит в сумму со знаком «плюс», для емкости I2Xc – со знаком «минус».
Пример составления баланса мощности
В цепи (рисунок 30) с параметрами:
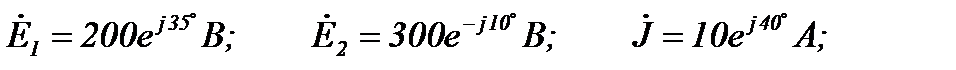
R1=15 Ом; R2=8 Ом; R3=20 Ом;
XL=20 Ом; XC1 =10 Ом; XC2 =15 Ом,
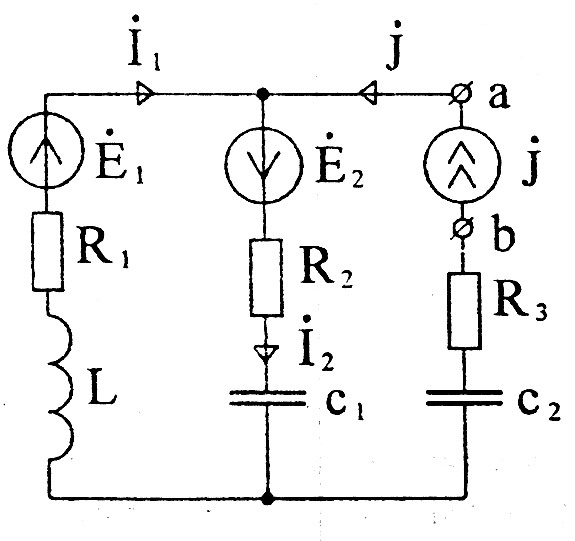
Рисунок 30
расчетным путем найдены токи:
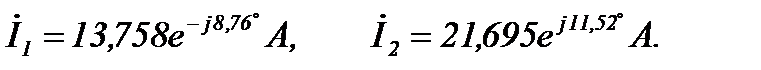
Для составления баланса мощности найдем напряжение 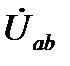 на зажимах источника тока (по второму закону Кирхгофа):
на зажимах источника тока (по второму закону Кирхгофа):
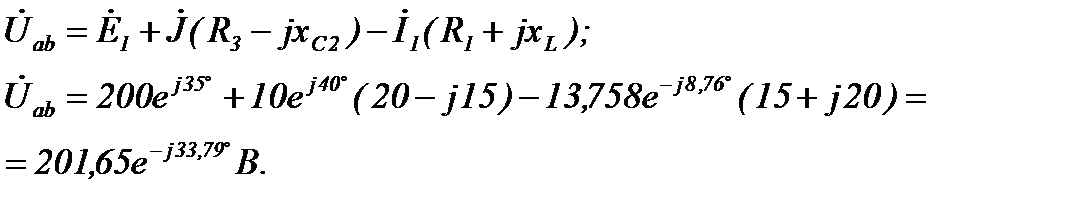
Тогда
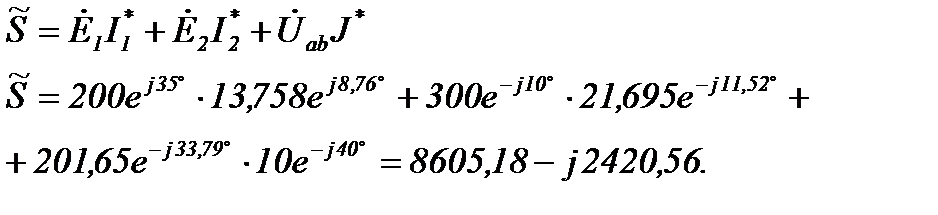
Отсюда
Рист=8605,18 Вт; Qист=-2420,56 ВАр.
Найдём активную мощность потребителей:
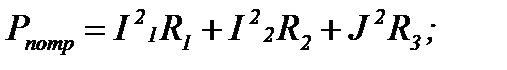
Рпотр=13,7582 . 15+21,6952 . 8+102 . 20=8604,62 Вт.
Реактивная мощность потребителей:
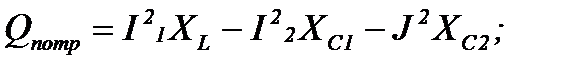
Qпотр=13,7582 . 20 - 21,6952 . 10 - 102 . 15= -2421,08 BАp.
Баланс мощности выполняется в пределах допустимой погрешности расчета (до 3%).
Задание на расчетно-графическую работу
Шифр задания состоит из трех чисел – номеров строк из табл. 5-7. Все три числа шифра соответствуют порядковому номеру студента в журнале (номеру 11 соответствует 1 вариант, 12 – 2 вариант, и т.д.). При решении задачи необходимо:
1. Используя данные табл. 5, 6, найти все токи электрической цепи:
а) методом контурных токов;
б) методом узловых потенциалов.
2. Составить баланс мощности.
3. Рассчитать ток в одной из ветвей цепи методом эквивалентного генератора. Номер ветви выбирается по первой цифре шифра.
Таблица 5
| Вариант |  |  |  |  |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  |
Таблица 6
| Вариант | Z1, Ом | Z2, Ом | Z3, Ом | Z4, Ом < |
